Les conseils de Wouf
Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.
Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.
Vivre seul, c'est prendre plaisir à manger du céleri rémoulade dans son papier d'emballage.
Triangle rectangle et cercle circonscrit, en quatrième 
Triangle rectangle et cercle
I Cercle circonscrit à un triangle rectangle
A propriété 1
Si un triangle est rectangle alors le centre de son cercle circonscrit est le milieu de l'hypoténuse.
B Propriété 1 bis
Si un triangle est rectangle alors son hypoténuse est un diamètre de son cercle circonscrit.
B Propriété 2
Si un triangle est rectangle alors l'hypoténuse a pour longueur le double de celle de la médiane issue du sommet de l'angle droit.
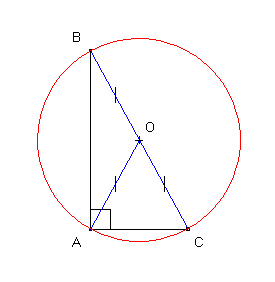
ABC est un triangle rectangle en A donc:
Le centre du cercle circonscrit à ABC est le point O, milieu de l'hypoténuse [BC]
La médiane [OA] relative à l'angle droit a pour longueur la moitié de l'hypoténuse [BC]
OA = OB = OC = BC/2
II Triangle inscrit dans un cercle
A propriété 1
Si un triangle est inscrit dans un cercle et a pour côté un diamètre de ce cercle alors ce triangle est rectangle. Le diamètre est son hypoténuse.
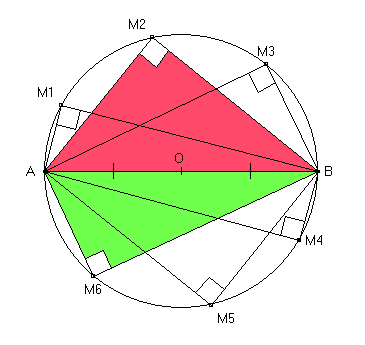
Le triangle AMB est inscrit dans le cercle de diamètre [AB] donc le triangle AMB est rectangle en M (et [MB] est l'hypoténuse)
B propriété 2
Dans un triangle si la médiane relative à un sommet à pour longueur la moitié du côté opposé à ce sommet alors le triangle est rectangle en ce sommet.
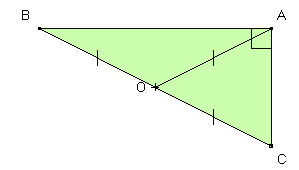
Dans le triangle ABC, la médiane issue de A, a pour mesure la moitié de la longueur du segment [BC] (opposé à A) donc le triangle ABC est rectangle en A.
Instructions officielles
CONTENU
Triangle rectangle et cercle circonscrit
COMPETENCES EXIGIBLES
- Caractériser le triangle rectangle par son inscription dans un demi-cercle dont le diamètre est un côté du triangle.
- Caractériser les points d'un cercle de diamètre donné par la propriété de l'angle droit.
COMMENTAIRES
Le cas où le demi-cercle n'est pas apparent est étudié.
La propriété:
"Dans un triangle rectangle, la médiane relative à l'hypoténuse a pour longueur la moitié de celle de l'hypoténuse" ainsi que sa réciproque sont mises en place.
L'essentiel des notions de mathématiques de la classe de 4ème.
Monoposte : 29,00 €
Un manuel de mathématiques de l'association Sésamath
pour les classes de 4e (édition 2011).
Prix du produit : 11,80 €
Exercices:
Sur mathenpoche (4ème, Géométrie, 1.Triangle rectangle)
Cette leçon au format PDF (Adobe Acrobat Reader)
Cette leçon au format Open Office zippée
Recherches associées. Résolues dans la page.
- triangle inscrit dans un cercle
- cercle circonscrit triangle rectangle
- exercice triangle rectangle et cercle circonscrit
- triangle circonscrit
- triangle dans un cercle
NEWS
- Page : https://site2wouf.fr/circonscrit.php
- Catégorie : Mathématiques
Etat des lieux du site2wouf.fr, été 2021.
Je profite des vacances et de la météo désastreuse dans le Pas-de-Calais en ce mois de juillet pour dresser un état des lieux du site. La première version date des débuts d'internet mais la version actuelle, avec ce nom de domaine est né en 2008, en janvier.
Environs quatre millions de pages ont été visitées depuis 2008. 84% des visiteurs sont français, le reste se partageant majoritairement entre les Etats Unis, et l' Afrique du Nord (6% pour la Tunisie)
Historiquement, les premières versions regroupaient surtout des pages de type leçons en Mathématiques couvrant l'ensemble du collège, ce sont ces pages qui continuent à générer le plus de visites aujourd'hui. (Ainsi la page d'entrée la plus fréquente est une leçon de trigonométrie pour les élèves de troisième. )
Aujourd'hui, à la dispositions des élèves et des collègues, vous pouvez trouver sur le site2wouf.fr :
- 3600 feuilles de problèmes gratuites en pdf pour tous (la résolution dépend du niveau)
- 2400 feuilles de problèmes gratuites en pdf adaptées au cyc
TIPS
Firefox est un très bon navigateur alternatif!
Lien de téléchargement dans la boite à outils du menu informatique...