Je suis candidat pour la révolution.
Trigonométrie dans le triangle rectangle
Dans le triangle rectangle ABC,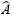 
est l'angle droit, le côté opposé à 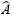(en face de 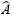) est [BC], c'est l'hypoténuse.
Si on s'intéresse à l'angle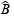 
:
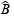
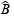
Si on s'intéresse à l'angle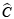 
:
Dans ABC un triangle rectangle en A, le cosinus, le sinus et la tangente de l'angle aigu sont donnés par les formules suivantes:
On a de même:
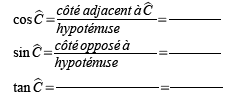
SOH CAH TOA n'est pas une formule magique mais une moyen mnémotechnique pour retenir les formules ci-dessus:
ABC est un triangle rectangle en A.
On donne AB = 5 cm et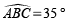 
.
Construire la figure en vraie grandeur.
Déterminer la longueur AC, arrondie au dixième de centimètre.
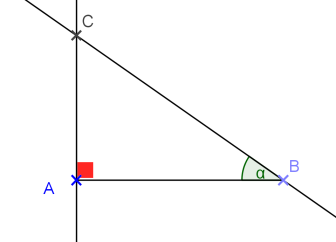
Dans le triangle ABC, rectangle en A
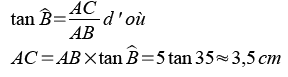
On peut contrôler la vraisemblance du résultat: (3,5 < 5 et 35 < 45)
Si a est un angle aigu d'un triangle rectangle:
cos 2 a + sin 2 a = 1
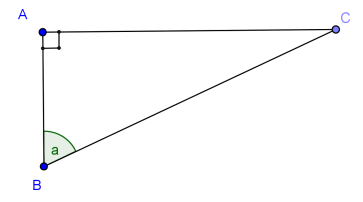
Dans ABC rectangle en A:
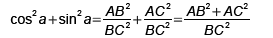
or d'après le théorème de Pythagore dans ABC rectangle en A:
AB²+AC²=BC²
donc
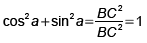
si a est un angle aigu d'un triangle rectangle:
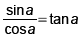
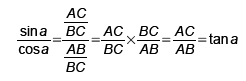
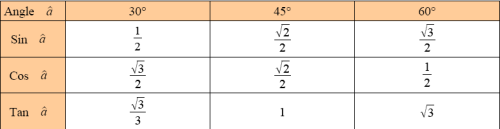
En choisissant un triangle rectangle adapté aux différentes situations, vérifier (retrouver) dans le tableau les valeurs exactes suivantes.
OFFICIEL
Triangle rectangle : relations trigonométriques
Connaître et utiliser dans le triangle rectangle des relations entre le cosinus, le sinus ou la tangente d'un angle aigu et les longueurs de 2 côtés du triangle.
Utiliser la calculatrice pour déterminer des valeurs approchées :
La définition du cosinus a été vue en 4ème . Le sinus et la tangente d'un angle aigu seront introduits comme rapports de longueurs ou à l'aide du quart de cercle trigonométrique.
On établira les formules:
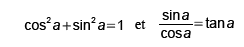
On n'utilisera pas d'autre unité que le degré décimal.
Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette leçon au format Open office (.zip)
Cette leçon au format PDF (Adobe Acrobat Reader)