Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Plus j'y pense, plus je me dis qu'il n'y a aucune raison pour que le carré de l'hypoténuse soit égal à la somme des carrés des deux autres côtés.
Frédéric Dard
La cité idéale (1475), Piero della Francesca
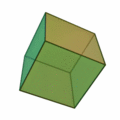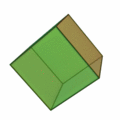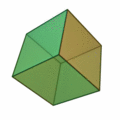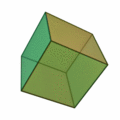
La perspective est l'art de représenter les objets à trois dimensions sur une surface plane, en tenant compte des effets de l'éloignement et de leur position dans l'espace par rapport à l'observateur. Pour l'artiste, certaines droites parallèles dans la réalité sont représentées comme des droites sécantes.
Par contre, en perspective cavalière, les parallèles dans la réalité sont représentées par des droites parallèles :
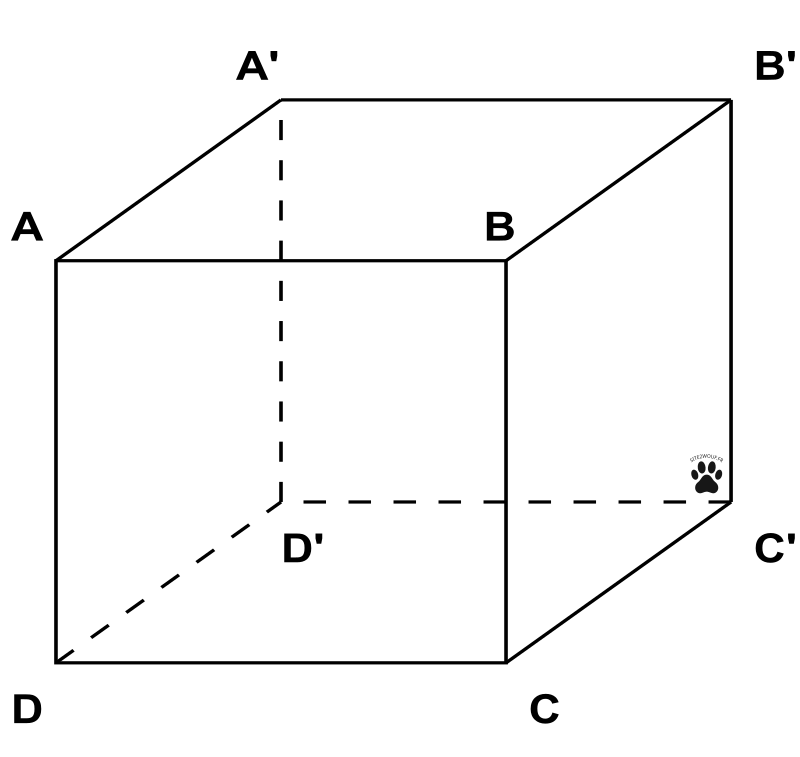
Par convention, on représente les arêtes invisibles en pointillés.
Ainsi la face au premier plan est, dans ce cube, le carré ABCD.
Merci patron
Merci patron
Quel plaisir de travailler pour vous
On est heureux comme des fous ♬
Chantaient Les Charlots...
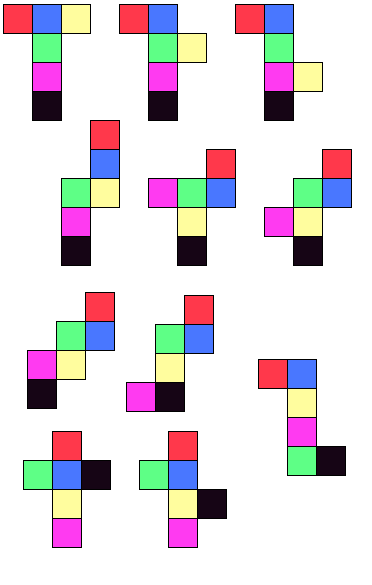
Patron:
(nom masculin)
Modèle pour la broderie, la tapisserie, pour fabriquer un objet. Pochoir pour le coloriage. Papier découpé servant de modèle pour tailler un vêtement.
Un patron d'un solide est une figure plane composée de polygones (appelés faces) qui sont disposés de telle manière qu'en les pliant le long de leurs arêtes communes, on peut reconstituer le solide en trois dimensions sans que les faces ne se chevauchent.
On considère le pavé droit ABCDEFGH représenté ci-dessous (figure non à l’échelle).
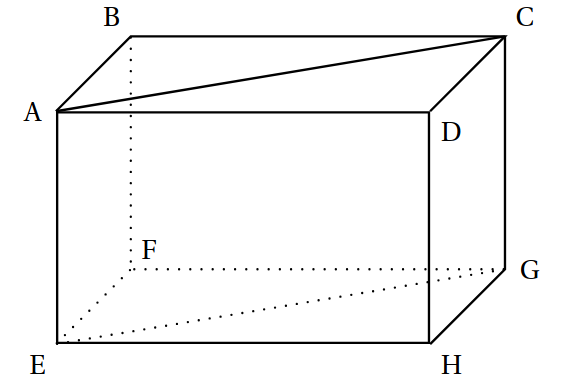Observer la figure, recopier et compléter le tableau suivant (sans justification) :
| Objet | Nature |
|---|---|
| Triangle ABC | … |
| Angle ^ABF | … |
| Quadrilatère ABFE | … |
| Angle ^ACG | … |
| Quadrilatère ACGE | … |
| Objet | Nature |
|---|---|
| Triangle ABC | Rectangle |
| Angle ^ABF | Droit |
| Quadrilatère ABFE | Rectangle |
| Angle ^ACG | Droit |
| Quadrilatère ACGE | Rectangle |
ABCDEFGH est un parallélépipède rectangle. On donne AE = 3 m; AD = 4 m; AB = 6 m.
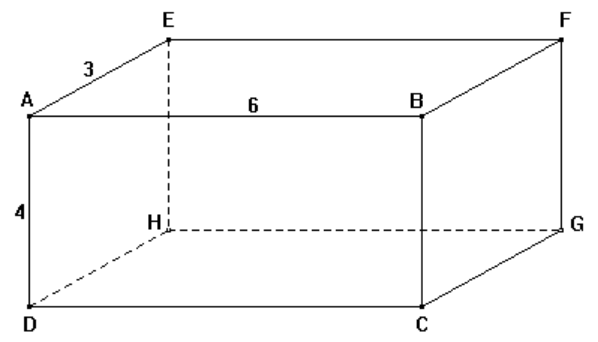
Le solide ABCDEFGH est un parallélépipède rectangle, donc toutes ses faces sont des rectangles (en particulier ABFE) et ses arêtes sont perpendiculaires deux à deux.
On a donc
(AE) ⊥ (AB)
Les droites (EH) et (AB) ne sont pas coplanaires (Pas dans le même plan).
Donc (EH) et (AB) ne sont pas sécantes.
Dans EFG rectangle en F, d'après le théorème de Pythagore:
EG² = EF² + FG²
EG² = 6² + 4²
EG² = 36 + 16
EG² = 52
EG = √52 m = 2√13 m
Dans EGC rectangle en G, d'après le théorème De Pythagore:
EC² = EG² + GC²
EG² = 52 + 3²
EG² = 52 + 9
EG² = 61
EG = √61 m
V = 3 × 4 × 6 = 72 m³
A = 2 × (3 × 4 + 3 × 6 + 4 × 6)
A = 2 × (12 + 18 + 24) = 2 × 54 = 108 m²
Ainsi les exercices classiques de l'espace ne sont que des exercices habituels. Il s'agit de trouver le plan dans lequel on travaille!
On appelle prisme droit un solide dont la base est un polygone et dont les faces latérales sont des rectangles.
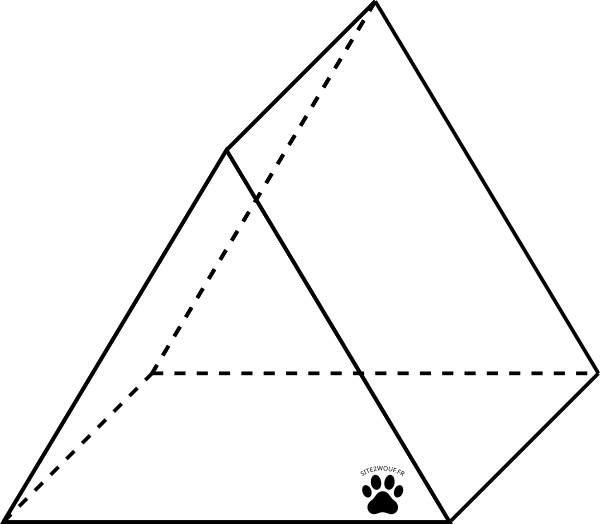
Le solide ci-dessus est un prisme droit à base triangulaire: Il a 6 sommets, 9 arêtes, et 5 faces.
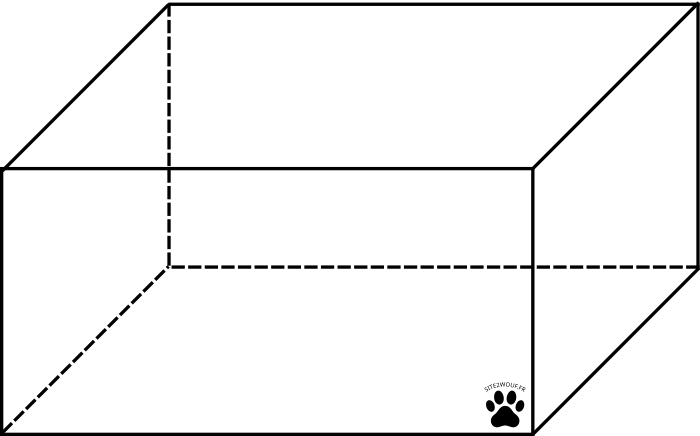
Le solide ci-dessus est un prisme droit à base rectangulaire: Il a 8 sommets, 12 arêtes, et 6 faces.
Quand on coupe un prisme droit par un plan parallèle à la base, la section trouvée est identique à la base:
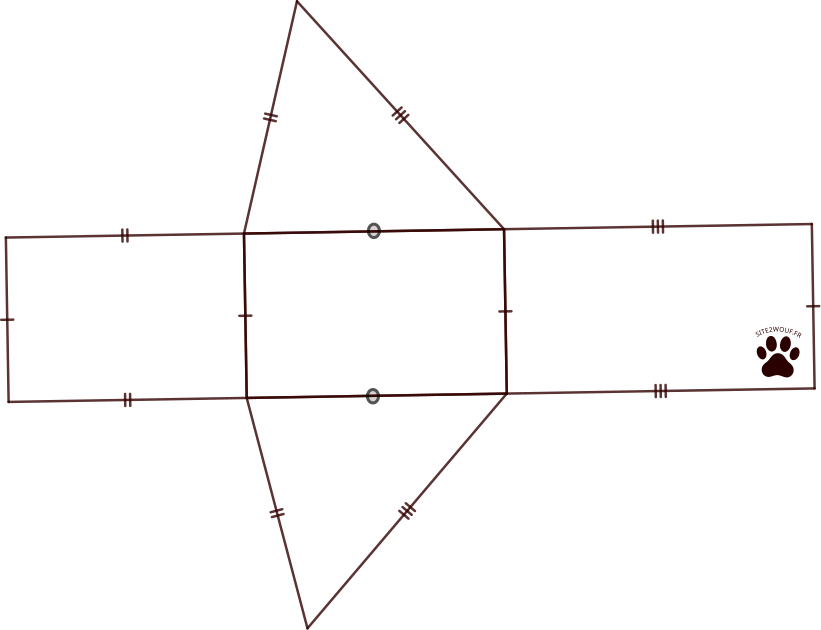
V= Bh
où B désigne l'aire de la base et h la hauteur du prisme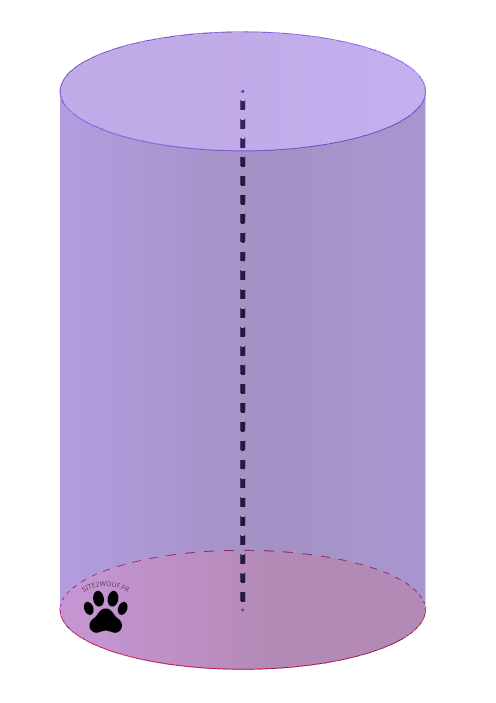
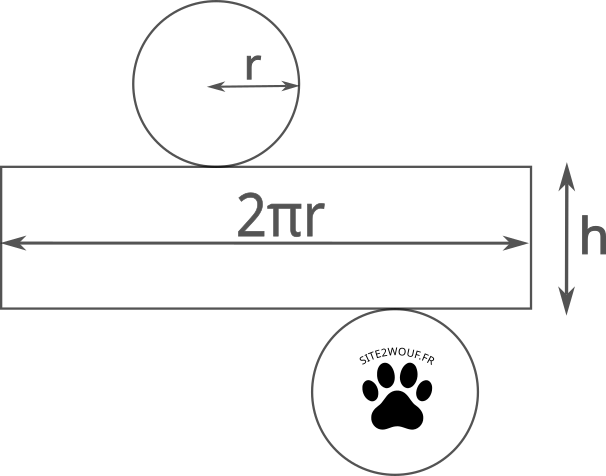
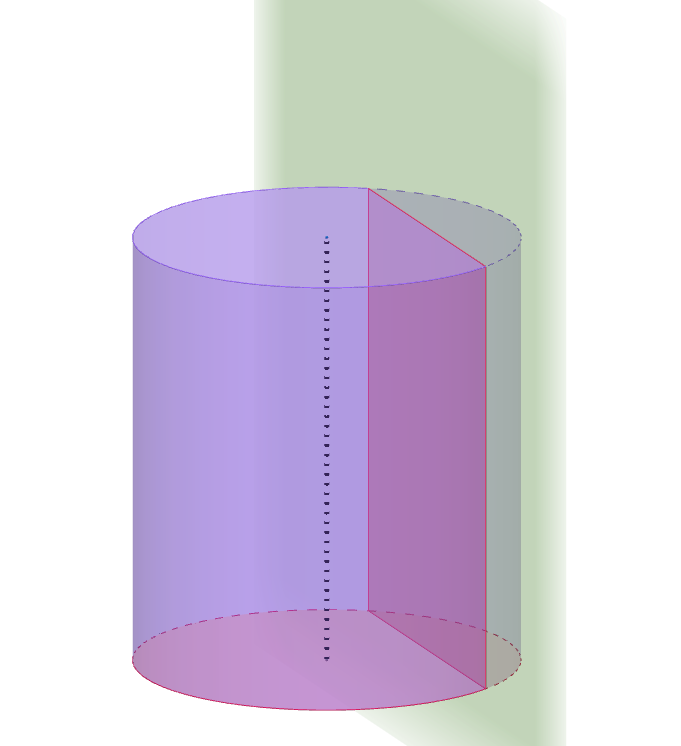
Quand on coupe un cylindre de révolution par un plan parallèle à la base, la section trouvée est un cercle de même rayon que celui de la base :
Quand on coupe un cylindre de révolution par un plan perpendiculaire à la base, la section trouvée est un rectangle dont un côté est égal à la hauteur du cylindre.
Comme pour le prisme droit (solide « sans pointe ») la formule est donnée par:
V= B x h = πr²h = π x r x r x h
(B désigne l'aire de la base)
Les pyramides ont pour base des polygones, et leurs faces latérales sont des triangles.
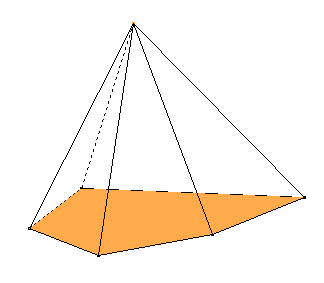
Quand on coupe une pyramide par un plan parallèle à la base, la section trouvée est de même nature que celle de la base:
Les pyramides régulières ont pour base des polygones réguliers:
et leurs faces latérales sont des triangles isocèles.
V = 1 3 × B × h
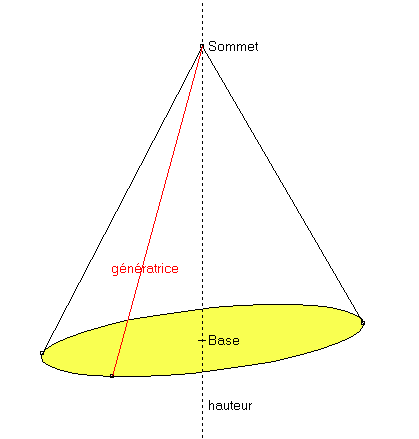
Quand on coupe un cône par un plan parallèle à la base, la section trouvée est un cercle de rayon inférieur à celui de la base.
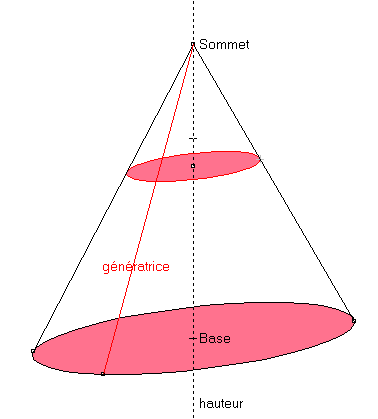
Tracer le patron d'un cône de révolution dont le base est un cercle de 3cm de rayon, et de hauteur 4cm.
Indice: La longueur de l'arc de cercle est égale à la circonférence du cercle de base
Dans ce triangle rectangle, d'après le théorème de Pythagore :
R² = r² + h² = 3² + 4² = 9 + 16 = 25
R = √25 = 5 cm
On va ensuite calculer l'angle ˇAOB :
| Longueur | Angle |
|---|---|
| 2πR = 10π | 360° |
| 2πr = 6π | ˇAOB |
ˇAOB = 360 × 6π 10π = 216°
V = 1 3 × B × h = 1 3 × π × r² × h
Dans un plan donné le cercle de centre O et de rayon r cm est constitué de tous les points à exactement r cm de O.
Dans un plan donné le disque de centre O et de rayon r cm est constitué de tous les points dont la distance à O est inférieure (ou égale) à r cm.
La sphère de centre O et de rayon r cm est constituée de tous les points de l'espace à exactement r cm de O.
La boule de centre O et de rayon r cm est constituée de tous les points de l'espace dont la distance à O est inférieure (ou égale) à r cm.
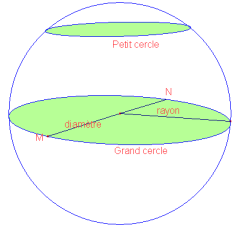
M et N sont diamétralement opposés
On ne peut pas construire le patron d'une sphère.
La section d'une sphère de centre O et de rayon R, par un plan est un cercle.
Si le plan passe par O, le cercle a pour rayon R
Sinon, son rayon r est inférieur à R
A = 4πR²
V = 4 3 πR³
Instructions officielles
On mettra en évidence les grands cercles de la sphère, les couples de points diamétralement opposés. On examinera le cas particulier où le plan est tangent à la sphère. On fera le rapprochement avec les connaissances que les élèves ont déjà de la sphère terrestre, notamment pour les questions relatives aux méridiens et parallèles.
Des manipulations préalables ( sections de solides en polystyrène par exemple) permettent de conjecturer ou d'illustrer la nature des sections planes étudiées. Ce sera une occasion de faire des calculs de longueur et d'utiliser les propriétés rencontrées dans d'autres rubriques ou les années antérieures.
A propos de pyramides, les activités se limiteront à celles dont la hauteur est une arrête latérale et aux pyramides régulières qui permettent de retrouver les polygones étudiés par ailleurs.
Le travail avec un formulaire qui n'exclut pas la mémorisation, permettra le réinvestissement et l'entretien d'acquis des années précédentes : aire des surfaces et volumes, des solides étudiées dans ces classes.
Des activités de comparaison d'aires, d'une part, et de volume, d'autre part, seront autant d'occasions de manipulations de formules et de transformations d'expressions algébriques. Ce travail prend appui sur celui fait en géométrie dans l'espace.
Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager: