
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Tout est permis en dedans.


Mémoire professionnel · 1993–1994
Échecs et Math — site2wouf.fr
Ce travail, réalisé pendant l'année scolaire 1993–1994, est mon mémoire professionnel. Comme chaque élève enseignant français, ma tâche était de réfléchir à diverses problématiques liées aux mathématiques ou à l'enseignement en général. Si beaucoup de collègues ont décidé de travailler sur des sujets mathématiques au sens strict (« la propriété de Pythagore et sa réciproque »), ma passion m'a dicté un tout autre choix : Échecs et math était le titre original, mais ce mémoire a été rendu sous le titre définitif : Mathématiques sur 64 cases.
Je remercie Monsieur Verrier d'avoir, à l'époque, accepté le tutorat d'un mémoire au sujet si peu orthodoxe.
Faire partager sa passion est un privilège. Lorsque celle-ci, par sa richesse, peut aider à l'épanouissement intellectuel de chacun, ce privilège devient un devoir. C'est pourquoi j'ai choisi de m'exprimer sur ce sujet, conscient des risques que j'encourais à quitter le chemin du classicisme.
En Occident le jeu, quand il n'est pas directement assimilé aux vices, prête à sourire : jouer n'est en aucun cas sérieux. En Orient par contre, le jeu rime avec sagesse ; le Go est une véritable institution au Japon, enseigné dans les écoles où l'on délivre des diplômes de progression. Dans les républiques slaves, les échecs sont enseignés jusqu'à l'université. Les GMI (Grands Maîtres Internationaux) y jouissent d'une influence politique considérable.
Pourtant à l'Ouest, de tout temps, des sociologues se sont penchés sur les bienfaits du jeu pour les tout jeunes enfants. Pauline Kergomard, Inspectrice Générale des Écoles Maternelles, n'écrivait-elle pas : Le jeu est le travail de l'enfant ?
Quatre institutrices du territoire de Belfort — Mmes Hutges, Isaac, Jucquin, Verbovski, assistées de Mme Chenderowsky — ont conduit une expérience sur le jeu d'échecs en grande section d'école maternelle. Les objectifs visés concernaient :
Si Pauline Kergomard a fait inscrire le jeu à la première ligne du programme officiel des Écoles Maternelles dès le 18 janvier 1887, il est totalement banni du système éducatif dès l'entrée au collège. Pourtant le jeu est formateur. Ayant la responsabilité du club d'échecs du CLG Gambetta d'Arras, j'ai pu cerner l'intérêt du jeu d'échecs en situation scolaire.
Toutes les disciplines scolaires, scientifiques ou littéraires, impliquent l'existence d'un Savoir. Savoir que l'enseignant se doit de « transmettre ». En réalité, souligne Antoine Prost dans son Éloge des pédagogues, le terme « transmettre » ne convient que pour des informations, non pour de véritables savoirs.
 Jean-Luc Chabanon, Grand Maître International · © Cyril Cavalié
Jean-Luc Chabanon, Grand Maître International · © Cyril Cavalié
Lorsqu'on initie un individu au jeu d'échecs, les mécanismes d'acquisition du savoir apparaissent clairement. Rien ne sert d'énumérer les différentes « marches des pièces », même clairement et plusieurs fois. Le cerveau humain est ainsi fait qu'il ne stockerait probablement rien. Et si, dans le meilleur des cas, le débutant retenait ces règles, il n'aurait reçu qu'un succédané de savoir : l'information. En aucun cas il ne serait devenu un joueur d'échecs. Le propre des vrais savoirs est qu'on ne peut les recevoir passivement — il faut les constituer progressivement, suivant son propre rythme.
Bien sûr, on ne peut se dispenser d'emmagasiner des informations. Il faut retenir faits, dates ou règles pour acquérir un savoir, mais cela ne suffit pas ! La problématique de la vie scolaire situe la cause des difficultés dans le désintérêt des élèves pour la monotonie de l'enseignement quotidien.
Sur la vingtaine de collégiens et lycéens qui participent régulièrement aux activités du club, seuls quatre étaient de parfaits débutants. Pour ceux-ci, la nécessité d'un apprentissage s'est concrètement fait sentir : on ne peut jouer aux échecs sans connaître les règles du jeu.
Pour les membres du club déjà habitués aux règles de base, le fait de pouvoir les « enseigner » aux autres avait aussi des avantages. Ils étaient fiers. Fiers de leur Savoir, fiers de pouvoir le partager, et pourquoi pas, par la suite, fiers d'apprendre ?
La suite normale de l'apprentissage des règles d'un jeu est le jeu par lui-même. Cependant, ce n'est pas parce qu'on connaît une recette par cœur que la cuisine sera réussie !
Une phase primordiale dans l'acquisition de connaissances est l'exercice d'application. Et ce qui est exceptionnel avec le jeu d'échecs, c'est que l'élève se rend compte de la nécessité de tels exercices.
Sur un échiquier vide, un cavalier placé en a1 doit se rendre en c3. En combien de coups minimum peut-il s'y rendre ?
Combien y a-t-il de chemins d'accès en quatre coups ?
Y a-t-il un rapport entre la couleur de la case de départ, celle de la case d'arrivée et la parité du nombre de coups reliant ces deux cases ?
Ce genre d'exercices n'est jamais inutile. Et la nécessité de « maîtriser » est, pour tous, évidente. On peut fonder l'espérance que la prise de conscience par l'élève de la rentabilité de ce type de travail dépasse le cadre du club d'échecs…

Enfin la récompense : l'élève en sait assez pour commencer à jouer. Dans la position initiale, les blancs disposent de 20 coups différents possibles (16 coups de pion et 2 coups pour chaque cavalier).
Pour la cadence « Blitz », les joueurs disposent de 5 minutes KO. Ainsi le temps de réflexion devient un paramètre à intégrer dans la procédure de choix.
Rappel : ce texte est écrit en 1993 :-)
Gérer son temps ne veut pas dire réfléchir plus vite, mais réfléchir mieux. En effet, une grande capacité de calcul n'implique pas nécessairement un niveau excellent aux échecs — sinon Deep-Thought avec ses MIPS serait champion du monde !
Toujours pas :-)
La partie a un peu avancé. Trente coups sont à la disposition du joueur. Pour chacun de ces coups, son adversaire disposera en moyenne de 34 possibilités. Cela implique déjà quelque 40 000 positions à évaluer — une paille pour un cerveau électronique, mais plus d'une heure de travail pour le joueur chevronné.
Réfléchir mieux implique la méthode dite des coups candidats : remplacer dans le processus analytique la liste des coups possibles par la liste des coups candidats.
Pour bien choisir, réduisons le nombre d'options. Ce « théorème » échiquéen n'a-t-il pas sa place dans l'éducation ?
L'enseignement est une relation entre personnes. La socialisation des élèves est donc nécessairement préalable à tout enseignement. Or le jeu est un magnifique outil de socialisation. Chacun joue avec les mêmes règles !
Deux joueurs du club pensaient de bonne foi qu'on pouvait, au premier coup, bouger deux pions différents. Du jour où ils décidèrent de s'intégrer au groupe, ils durent se plier aux règles officielles. Ils se socialisaient.
Le respect de l'adversaire est également important. Tous deux jouent l'un contre l'autre, mais ensemble.
Nul enseignant n'aura la bêtise de prétendre que dans sa discipline, il n'a plus rien à apprendre. Il en est de même pour le jeu d'échecs.
À la fin du XVe siècle, Lucena et Damiano publiaient déjà des livres d'échecs. Philidor publia en 1749 son célèbre Analyse du jeu des échecs. Au XIXe siècle, les néo-romantiques Réti, Nimzowitch et Tartacover formulèrent d'importants principes stratégiques.
Viktor Kortchnoy reconnaissait en échouant lors d'un cycle de qualification qu'il manquait de préparation. On ne sait jamais jouer aux échecs, on apprend.
Il n'est pas nécessaire que le travail soit triste pour être fécond. Travailler les échecs est plaisant, jouer aux échecs est plaisant. Ces îlots d'intérêts donnent aux élèves la possibilité de quitter leur rôle de spectateurs obligés pour devenir acteurs volontaires. Et cela fonctionne car l'élève y trouve du plaisir !
Un point commun entre les échecs et les mathématiques est la notion de problème. Parfois des mathématiciens de renom se posent des problèmes d'échecs.
Léonard Euler s'est consacré au problème de la « rosace du cavalier » : le cavalier doit passer par toutes les cases de l'échiquier, en ne visitant chacune qu'une seule fois.
Comme activité préparatoire au maniement des vecteurs, j'ai proposé aux élèves de 3e :
a) En un mouvement
1. Le cavalier est situé en A(3 ; 4), on le déplace en H image de A par la translation de vecteur MN (1 ; 2). Quelles sont les coordonnées de B ? Comment les obtient-on à partir de celles de A et de MN ? Plus généralement : si A(x ; y), quelles sont les coordonnées de B ?
2. On déplace un cavalier du point C(5 ; 2) au point D(3 ; 3). Quelles sont les coordonnées du vecteur de cette translation ?
3. Compléter : soient A(xA ; yA) et B(xB ; yB). Les coordonnées du vecteur AB sont __________
b) Recherche d'un chemin
1. Le cavalier est situé en E(1 ; 1). Trouver deux déplacements successifs qui amènent le cavalier en F(2 ; 2). Quelles sont les coordonnées du vecteur EF ?
2. Mêmes questions pour aller de G(1 ; 2) à H(6 ; 7).
3. Si U(x ; y) et V(x′ ; y′), alors les coordonnées du vecteur U+V sont _______
Cette activité est riche : coordonnées d'un vecteur, somme de vecteurs, translations, composée de translations. Les échecs ne sont ici autre chose que 64 cases à la disposition des Mathématiques.
De combien de manières peut-on disposer huit Dames sur l'échiquier de façon qu'en aucun endroit elles ne se menacent l'une l'autre ? Gauss n'a trouvé que 72 positions. La réponse exacte — 92 — a été trouvée plus tard.
 Une des 92 solutions
Une des 92 solutions
J'ai proposé aux élèves de Terminale C un problème connexe : de combien de manières peut-on disposer huit Tours sans qu'elles se menacent ? Le raisonnement :
Il y a donc 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 8! manières.
Dans Des échecs à l'infini, Anatoly Karpov et Evgueni Guilk (docteur en mathématiques) ont considéré les échecs comme « un monde complexe, aux trois dimensions : art, sport et science ».
L'étude suivante de Réti illustre les propriétés géométriques de l'échiquier :
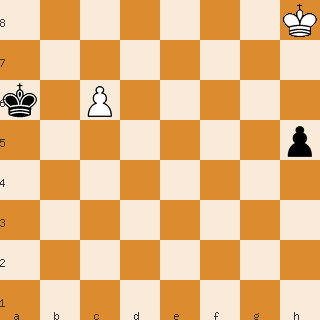
Les Blancs jouent et font nulle.
Le roi arrête le pion en utilisant une propriété géométrique de l'échiquier : la ligne la plus courte entre deux cases n'est pas toujours la ligne droite. Cette « découverte mathématique » restera sous le nom de manœuvre de Réti.
Mathématiciens et joueurs d'échecs ont un souci commun : la création d'objets. Le point à l'infini de la géométrie projective ou le concept de pion faible « nimzowitchien » sont deux exemples d'objets virtuels créés en conformité avec un schéma de pensée.
Un élève de 3e dispose de 4 outils pour démontrer qu'un triangle est rectangle :
Un joueur d'échecs dispose d'outils analogues pour attaquer le roque ennemi :
« Mat en 2 coups » signifie en réalité : « démontrer que les blancs matent le roi noir en 2 coups maximum quelles que soient les réponses noires. »
Si les blancs jouent tel coup, alors les noirs ont ces n possibilités. Pour la première, les blancs répondent Cxf7 mat. Pour la deuxième, TxT mat… Et certains problémistes de conclure c.q.f.d.
En géométrie pure, une démonstration est souvent bâtie sur un cas général auquel viennent se greffer des cas particuliers. Dans un problème d'échecs, on a une variante principale et des variantes secondaires — qui font d'ailleurs le charme de l'étude.
Je conseille souvent à un élève devant une figure de regarder les figures. C'est en prenant conscience des figures clés, tout en gardant en tête le but poursuivi, que naît l'idée, le plan, la première esquisse de démonstration.
La similitude avec le jeu d'échecs est évidente : le joueur se doit de définir un plan. C'est l'étude des structures de la position qui conduit au choix du plan.
Aux échecs comme en mathématiques, il arrive qu'on sente confusément quelque chose. « Cela sent Thalès », me disait un élève. Dans certaines positions, l'intuition prend le relais quand l'analyse exhaustive est impossible. « Le sacrifice en f7 devrait marcher. »
Et effectivement cela « marche »… Parfois.
C'est facile, mais il fallait y penser !
Aux échecs, c'est l'imagination qui fait la différence entre l'amateur et le maître.
Avant de jouer un coup, il convient d'avoir acquis la conviction que ce coup était sinon le meilleur, du moins assez bon. Réfléchir avant d'agir est également nécessaire en mathématiques !
Certains élèves ont le mauvais réflexe de commencer par des calculs baroques avant même de savoir ce qu'ils cherchent. On peut admettre dans une certaine mesure que le jeu d'échecs forme le raisonnement.
Être rigoureux n'est pas inné. Sur un échiquier, absolument tout doit être vérifié. Une faute de rigueur peut changer une partie gagnée en une partie perdue. La sanction ne se fait pas attendre.
Échecs et Mathématiques sont donc de proches cousins. Rien d'étonnant à cela si l'on évoque la légende liée à la création de ce noble jeu :

La légende liée à la création du jeu d'échecs
L'inventeur du jeu demanda un grain de blé pour la première case, deux pour la seconde, quatre pour la troisième et ainsi de suite jusqu'à la 64e. L'empereur ordonna à son ministre de répondre à cette requête si modeste… En apparence !
On peut alors se permettre de supposer que l'inventeur était mathématicien…
En 1993, ce mémoire ironisait : « sinon Deep-Thought avec ses MIPS serait champion du monde ! » La blague a mal vieilli. En 1997, Deep Blue bat Kasparov lors d'un match officiel. En 2017, AlphaZero apprend les échecs de zéro par auto-jeu en moins de quatre heures, puis écrase Stockfish sans jamais avoir consulté une partie humaine. Aujourd'hui, aucun humain ne peut rivaliser avec les meilleures IA. La prédiction de 1993 s'est retournée — et d'une façon que personne n'avait vraiment anticipée.
La légende évoque une requête « si modeste… en apparence ». L'inventeur demandait la somme d'une suite géométrique de raison 2 sur 64 termes :
Si tu es lycéen(ne) et que tu réfléchis à un sujet de Grand Oral du baccalauréat autour des mathématiques, du jeu d’échecs ou plus largement du raisonnement logique, ce mémoire peut te servir de point d’appui. Il ne s’agit pas de le réciter ni de le résumer, mais de t’en inspirer pour construire ta propre réflexion : comment un jeu peut aider à penser, à raisonner, à anticiper, à faire des choix ? En quoi les échecs mobilisent-ils des compétences mathématiques comme la logique, la combinatoire, la stratégie ou la résolution de problèmes ? Tu peux aussi élargir la réflexion à des questions actuelles : la place du jeu dans les apprentissages, le lien entre mathématiques et intelligence artificielle, ou encore le rôle des outils ludiques pour développer l’esprit critique. L’essentiel, pour le Grand Oral, est de montrer que tu as compris les enjeux du sujet et que tu es capable de les relier à des exemples concrets et à ton propre parcours.
Partager :