Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Sometimes a cigar is just a cigar.
Freud
On dit qu'un tableau est un tableau de proportionnalité si les termes de la deuxième ligne s'obtiennent en multipliant ceux de la première par un même nombre. Ce nombre s'appelle le coefficient de proportionnalité.
Exemple:
| Côté d'un carré en cm | 1 | 2 | 3 | 4 | 5 | 10 | 4.1 |
| Périmètre de ce carré en cm | 4 | 8 | 12 | 16 | 20 | 40 | 16.4 |
Ce tableau est un tableau de proportionnalité.
Le coefficient est 4
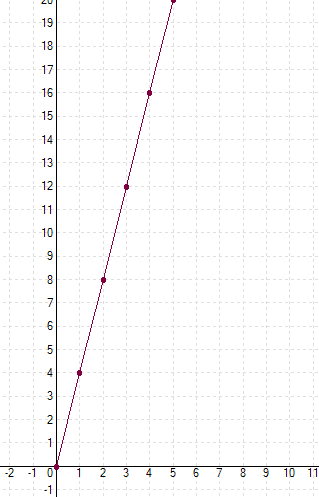
Les points du graphique sont alignés avec l'origine du repère.
Le coefficient de proportionnalité 4 peut être « lu » sur le graphique:
Si on avance de 1 sur l'axe des abscisses, on monte(+) de 4 sur l'axe des ordonnées
L'usine représente la fonction linéaire f qui a x associe 4x
On note:
f: x -> 4x ou f(x)=4x
on a:
f: 5 -> 20 qu'on écrira f(5)=20.
L'usine f (la fonction linéaire) transforme la matière première (les nombres) pour « fabriquer » de nouveaux nombres (qu'on appelle images)
f(3)=12 peut se traduire par:
Par la fonction linéaire f, l'image du nombre 3 est le nombre 12.
Ainsi à chaque situation de proportionnalité correspond une fonction linéaire. La représentation graphique d'une fonction linéaire est donc une droite passant l'origine du repère.
Un magasin augmente le prix de tous ses produits de 15%, remplir le tableau suivant:
| Prix avant l'augmentation en euros | 24.40 | 48.80 | 976 |
| Augmentation en euros | 3.66 | 7.32 | 146.40 |
En pratique on peut utiliser la fonction linéaire f: x -> 0,15x pour calculer l'augmentation de 15% (15%=15/100=0,15) sur un prix donné. f(100)=15 , f(0)=0 etc.
Remplir le tableau suivant:
| Prix avant l'augmentation en euros | 24.40 | 48.80 | 976 | 25 | 28.80 |
| Prix après l'augmentation en euros | 28.06 | 56.12 | 1122.4 | 28.75 | 33.12 |
En pratique on peut utiliser la fonction linéaire g: x -> 1,15x pour calculer le nouveau prix après une augmentation de 15% En effet :
x+0,15x=(1+0,15)x=1,15x
g(100)=115, g(0)=0 etc.
D'autres situations classiques de problèmes sont en rapport avec la proportionnalité et les fonctions linéaires:
Monsieur Durand fait sa promenade hebdomadaire à vélo. Il se rend au sommet du mont A à 30km de son domicile à 20km/h (ça monte) puis revient pas la même route à 30 km/h (ça descend!).Quelle est sa vitesse moyenne lors de sa promenade, en km/h puis en m/s?
Étudions «sa promenade»:
| Distance en km | 30 | 20 |
| Temps en heure | t | 1 |
t=30/20=1,5h. (On peut aussi utiliser la formule V=d/t)
Le temps de l'aller est une heure et demie.
| Distance en km | 30 | 30 |
| Temps en heure | t | 1 |
Le temps du retour est évidemment 1 heure
Nous allons calculer la vitesse moyenne:
| Distance en km | 60 | d |
| Temps en heure | 2.5 | 1 |
d=60/2,5=24
La vitesse moyenne sur le trajet total est donc 24km/h (Étonnant non?)
| Distance en m | 24000 | d |
| Temps en secondes | 3600 | 1 |
d=24000/3600=240/36=20/3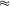 
6,67m/s
La vitesse moyenne est environ 6,67 m/s sur le trajet total.
Il suffit de retenir que:
Pour une échelle de 1/250 000 signifie que 1 unité sur le plan représente 250 000 unités dans la réalité et de calculer la quatrième proportionnelle, en fonction de l'énoncé.
| Distance en m sur dessin | 1 | d? |
| Distance en dans la réalité | 250 000 | D? |
Utiliser, dans le plan muni d'un repère, la caractérisation de la proportionnalité sous la forme d'alignement de points avec l'origine.
Utiliser l'égalité d = vt pour des calculs de distance parcourue, de vitesse et de temps. Changer d'unités de vitesse (mètre par seconde et kilomètre par heure).
Mettre en oeuvre la proportionnalité dans des situations simples utilisant à la fois des pourcentages et des quantités ou des effectifs.
On fera travailler les élèves à la fois sur des exemples et des contre-exemples de situations de proportionnalité.
Les situations où interviennent des vitesses moyennes constituent des exemples riches où le traitement mathématique s'avère particulièrement pertinent, comme l'étude de la vitesse moyenne d'un trajet sur un parcours de 60 km, où l'aller se parcourt à 20 km. h-1 et le retour à 30 km. h-1. Les compétences exigibles se réduisent aux vitesses mais d'autres situations de changements d'unités méritent d'être envisagées: problèmes de change monétaire, consommation de carburant d'un véhicule en litres pour 100 kilomètres ou en kilomètres parcourus par litre.
En liaison avec d'autres disciplines (géographie,...), la notion d'indice pourra être présentée comme un cas particulier du coefficient de proportionnalité, donnant lieu à illustrations et calculs mais en aucun cas à des développements théoriques.
Des situations issues de la vie courante ou des autres disciplines demandent de mettre en oeuvre à la fois un coefficient de proportionnalité, sous forme de pourcentage ou d'indice, et des quantités ou des effectifs. Par exemple, connaissant le pourcentage d'un caractère dans deux groupes d'effectifs différents,déterminer le pourcentage obtenu après réunion des deux groupes.
Le Manuel iParcours Maths 4ème reprend le programme officiel 2016 de mathématiques avec cours, activités de découverte et exercices d'entrainement.
Le manuel : 15,95 €