Tout le monde est égal devant le slip.
Jan Bucquoy
On appelle médiatrice d’un segment la droite perpendiculaire à ce segment en son milieu.
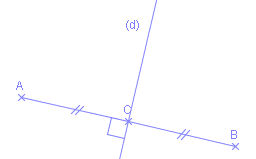
La droite (d) est perpendiculaire au segment [AB] en son milieu, la droite (d) est donc la médiatrice du segment [AB]
La médiatrice d’un segment est un axe de symétrie de ce segment.
Si un point appartient à la médiatrice d’un segment alors il est situé à égale distance des extrémités de ce segment.
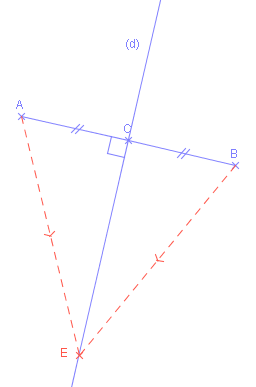
Le point E appartient à la médiatrice du segment [AB] donc le point E est équidistant des points A et B.
Si un point est équidistant des extrémités d’un segment alors il appartient à la médiatrice de ce segment.
Si le point E est équidistant des points A et B, alors le point E appartient à la médiatrice du segment [AB].
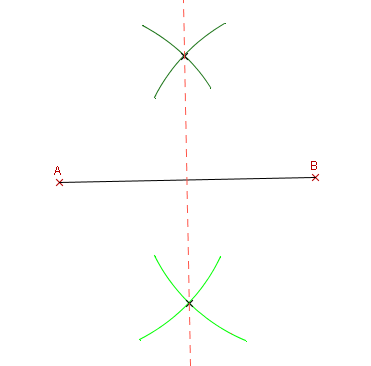
On trace deux arcs de cercle, de même rayon, et de centres les extrémités du segment. Ils se coupent en deux points appartenant à la médiatrice de ce segment.
Les médiatrices d'un triangles sont concourantes en un point: le centre du cercle circonscrit au triangle.
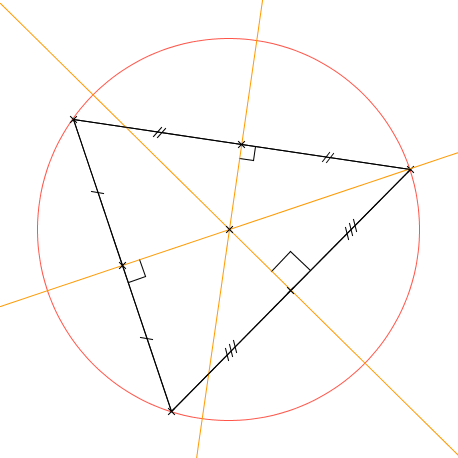
en exercice
La bissectrice d’un angle est la droite qui partage l’angle en deux angles égaux.
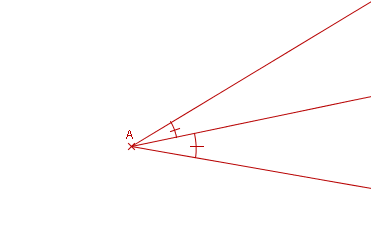
La bissectrice est l’axe de symétrie de cet angle.
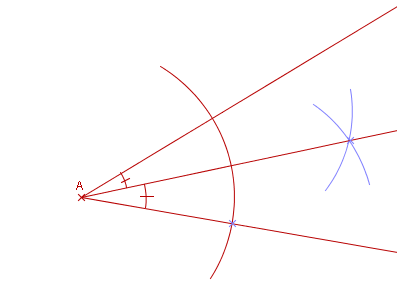
On trace deux arcs de cercles de même rayon et dont les centres sont deux points appartenant aux côtés de l'angle, équidistants du sommet. Ces arcs se coupent, à l'intérieur de l'angle, en un point appartenant à la bissectrice de l'angle.
Si un point appartient à la bissectrice d'un angle, alors il est équidistant des côtés de l'angle
Si un point est équidistant des deux côtés d'un angle, alors il appartient à la bissectrice de cet angle
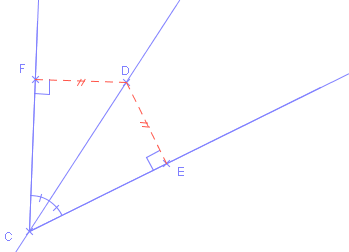
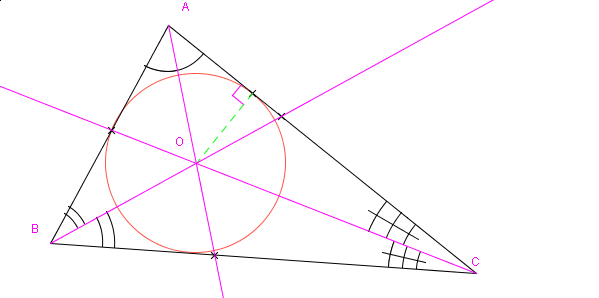
Les bissectrices (intérieures) d'un triangles sont concourantes en un point: le centre du cercle inscrit au triangle.
en exercice
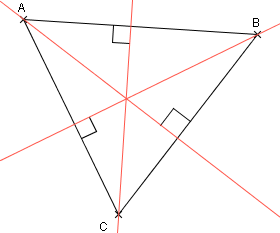
Dans un triangle on appelle hauteur issue d'un sommet, la droite passant par ce sommet et perpendiculaire au côté opposé à ce sommet.
Les hauteurs d'un triangle sont concourantes en un point: l'orthocentre du triangle
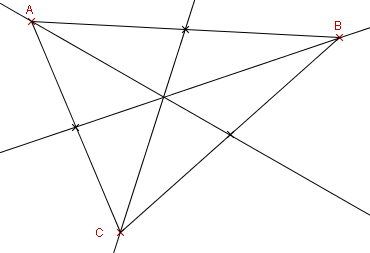
Dans un triangle on appelle médiane issue d'un sommet, la droite passant par ce sommet et le milieu du côté opposé à ce sommet.
Les Médianes d'un triangle sont concourantes en un point: le centre de gravité du triangle
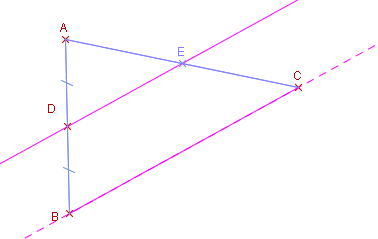
Dans un triangle, la droite qui passe par les milieux de deux côtés est parallèle au troisième côté.
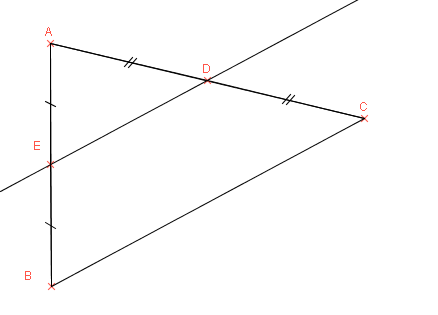
Dans un triangle, le segment qui joint deux milieux est égale à la moitié de la longueur du troisième côté.
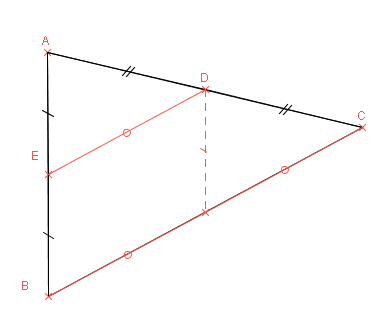
Dans un triangle, la droite qui passe par le milieu d’un côté et qui est parallèle à un second côté, coupe le troisième côté en son milieu.
En classe de quatrième, la représentation d'objets géométriques usuels du plan et de l'espace, le calcul de grandeurs attachées à ces objets demeurent des objectifs majeurs. S'y ajoutent de nouvelles caractérisations pour certains d'entre eux (triangle rectangle, cercle, bissectrice).
Dans le plan, les travaux portent sur les figures usuelles déjà étudiées (triangle, cercle, quadrilatères particuliers), pour lesquelles il est indispensable de continuer à faire fonctionner les résultats mis en place.
L'étude plus approfondie du triangle rectangle et d'une nouvelle configuration (celle de triangles déterminés par deux droites parallèles coupant deux sécantes) permet d'aborder quelques aspects numériques fondamentaux de la géométrie du plan.
Certaines propriétés géométriques d'un agrandissement ou d'une réduction d'une figure sont également étudiées. L'effet sur les aires et les volumes n'est abordé qu’en classe de troisième.
Les activités de découverte, d'élaboration et de rédaction d'une démonstration sont de natures différentes et doivent faire l'objet d'une différenciation explicite. Le travail sur la caractérisation des figures usuelles est poursuivi, en veillant à toujours la formuler à l'aide d'énoncés séparés.
Dans l'espace, les travaux sur les solides étudiés exploitent largement les résultats de géométrie plane.
Connaître et utiliser les théorèmes suivants relatifs aux milieux de deux côtés d'un triangle :
Ces théorèmes peuvent être démontrés en utilisant la symétrie centrale et les propriétés caractéristiques du parallélogramme ou les aires.
Cette caractérisation permet de démontrer que les trois bissectrices d'un triangle sont concourantes et justifie la construction du cercle inscrit. L'analogie est faite avec le résultat concernant les médiatrices des trois côtés du triangle vu en classe de cinquième.
Le Manuel iParcours Maths 4ème reprend le programme officiel 2016 de mathématiques avec cours, activités de découverte et exercices d'entrainement.
Le manuel : 15,95 €