La nostalgie, c'est comme les coups de soleil : ça fait pas mal pendant, ça fait mal le soir.
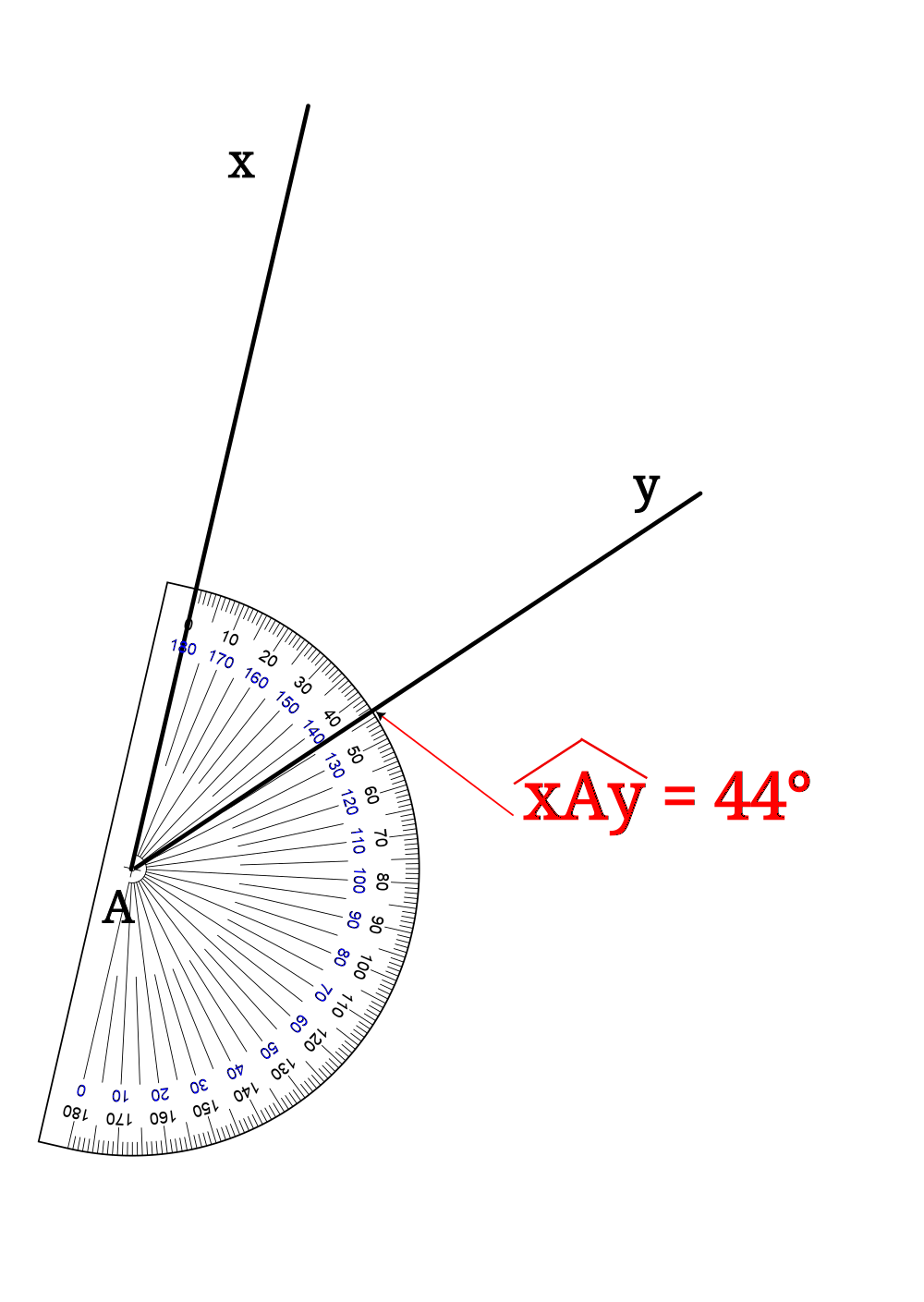
En cycle 3, on a appris à se servir du rapporteur, c'est l'outil qu'il faut ici impérativement maîtriser!
En cas de doute n'hésitez pas à relire la leçon!
On commence par faire un rapide schéma pour avoir une idée de la place nécessaire. Au propre on trace le segment connu. Les angles nous permettent alors le tracé de deux demi-droites qui se coupent au dernier sommet
On commence par faire un rapide schéma pour avoir une idée de la place nécessaire. Au propre on trace un des segments connus (On choisit souvent le plus grand). Puis après avoir tracer l'angle, il reste à tracer le deuxième segment connu.
Voir le cahier d'exercices
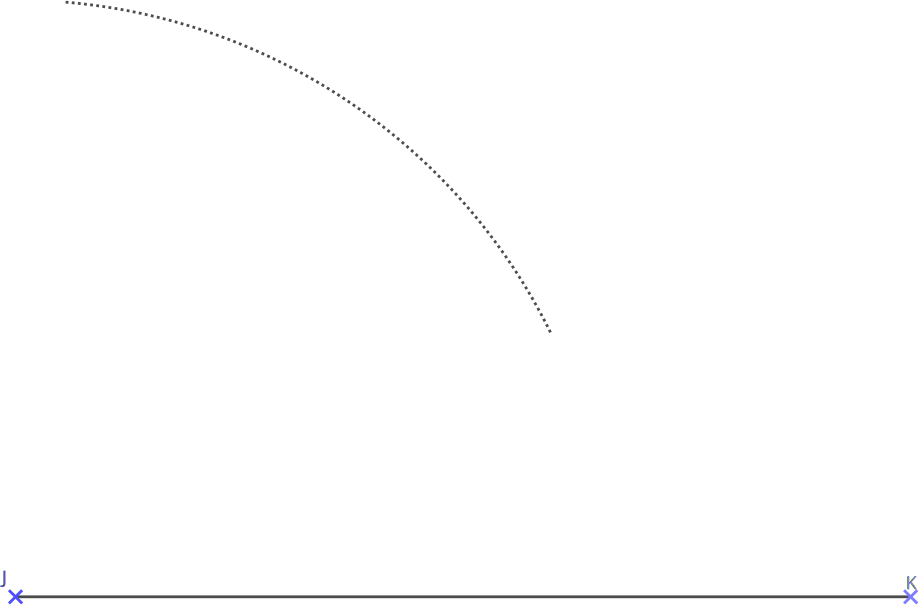
On commence par faire un rapide schéma pour avoir une idée de la place nécessaire. Au propre on trace l'un des segments (On choisit souvent le plus grand).
On se rappelle alors la définition du cercle : Le cercle de centre O et de rayon 5cm (par exemple) est l'ensemble des points situés à 5cm de O.
Il nous reste donc deux arcs de cercle à tracer, arcs qui se coupent au troisième sommet du triangle.
Les plus observateurs d'entre vous ont remarqué que, dans la consigne de construction, il y avait, entre guillemets : si possible.
On pouvait déjà comprendre que tous les triangles ne sont pas constructibles connaissant trois longueurs.
Pourquoi?
Dans un triangle, la longueur d'un côté est inférieure à la somme des longueurs des deux autres côtés.
S'il y a égalité, les trois points sont alignés.
Pour vérifier si on peut construire un triangle, il suffit de vérifier que la plus grande longueur est inférieure à la somme des longueurs des deux autres côtés.
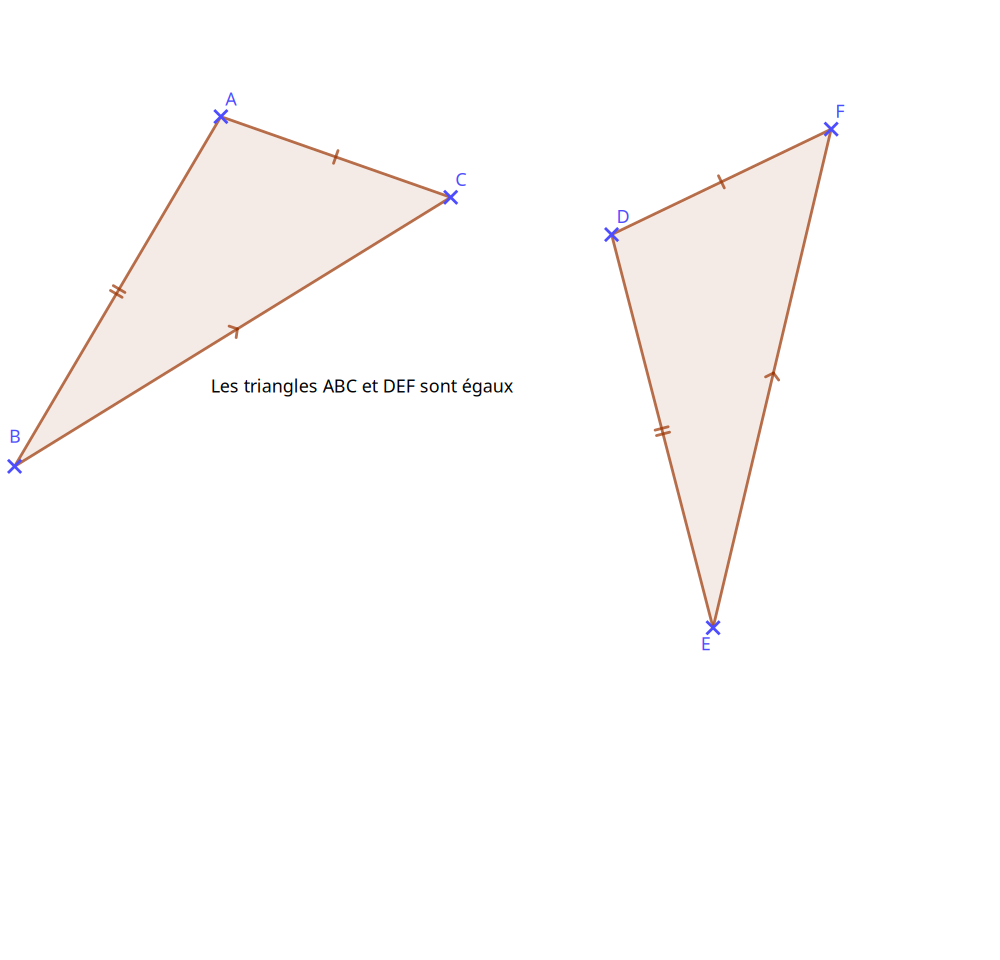
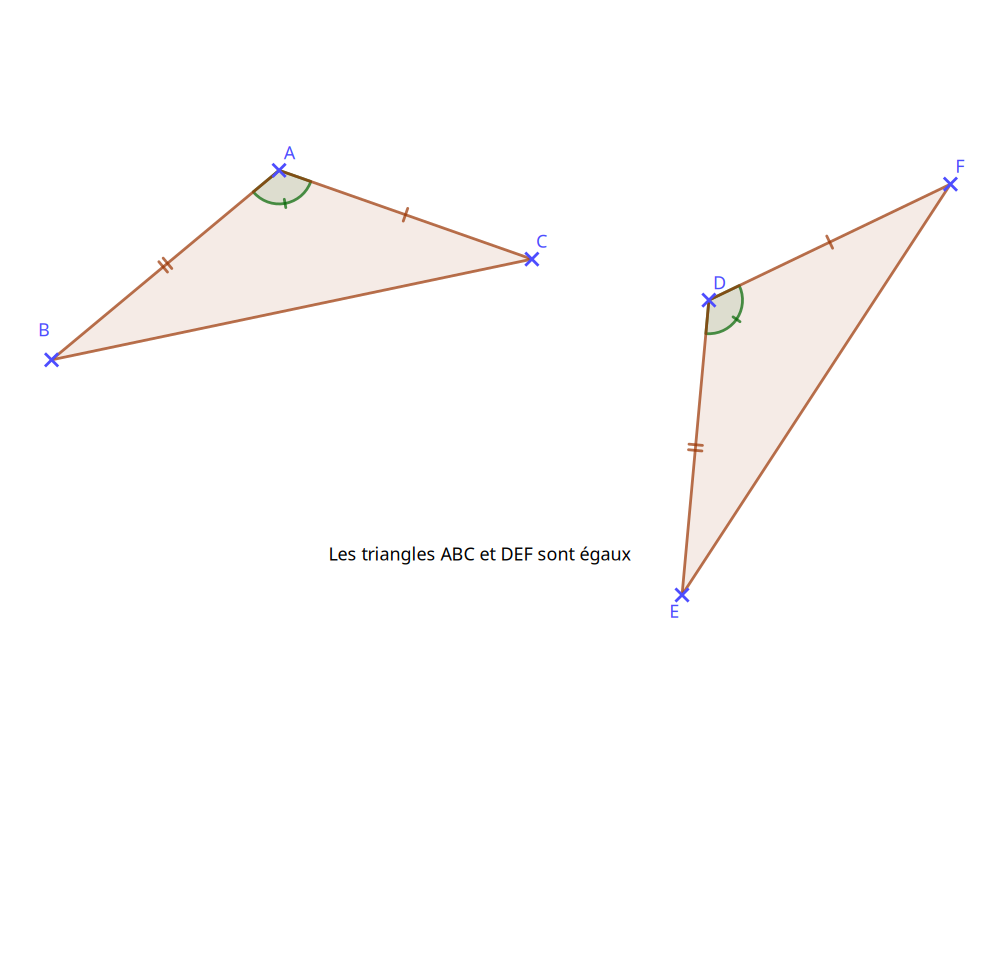
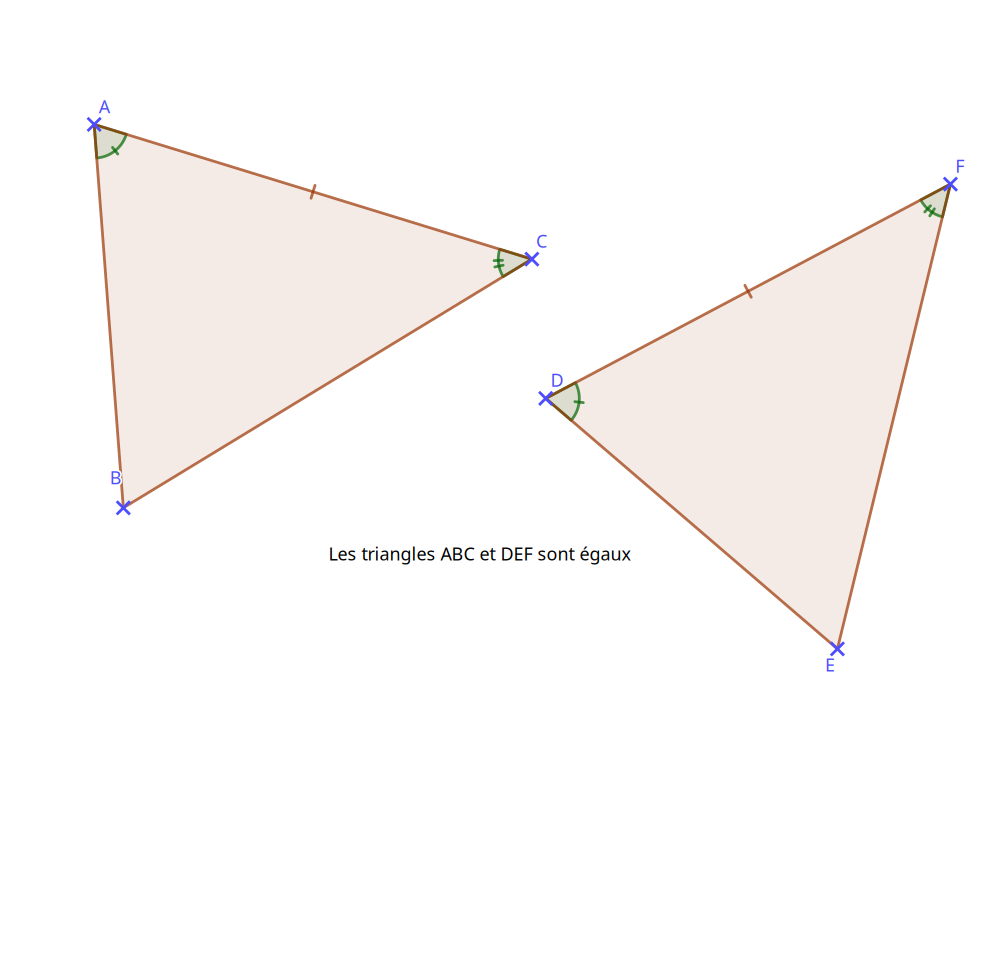
Deux triangles sont égaux lorsqu'on peut les superposer par déplacement ou par retournement.
Si deux triangles sont égaux alors ils ont leurs trois côtés et leurs trois angles de même mesure.
On appelle ça des propriétés caractéristiques . (Elles sont aussi puissantes que la définition !)
Au cycle 3, les élèves ont découvert différents objets géométriques, qui continuent à être rencontrés au cycle 4. Ils valident désormais par le raisonnement et la démonstration les propriétés qu'ils conjecturent.
Les définitions et propriétés déjà vues au cycle 3 ainsi que les nouvelles propriétés introduites au cycle 4 (caractérisation angulaire du parallélisme, somme des angles d’un triangle, inégalité triangulaire, théorèmes de Thalès et de Pythagore) fournissent un éventail d'outils nourrissant la mise en œuvre de raisonnements et démonstrations.
De nouvelles transformations (symétries centrales, translations, rotations, homothéties) font l'objet d'une première approche, basée sur l’observation de leur effet sur des configurations planes, essentiellement à partir de manipulations concrètes (papier calque, papier pointé, quadrillage, etc.) ou virtuelles (logiciel de géométrie dynamique). L’objectif est d’installer des images mentales qui faciliteront ultérieurement l’analyse de figures géométriques ainsi que la définition ponctuelle des transformations étudiées.
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €