In theory, there is no difference between theory and practice. In practice, there is.
Chuck Reid (sur mon T shirt!)
Étymologiquement, une expression littérale est une expression qui contient une ou plusieurs lettres.
k(a+b)=ka+kb (vu en 5ème)
Plutôt que retenir que l'aire d'un rectangle est le produit de la longueur par la largeur, on peut retenir: A=L × l
Paul a 6 billes de plus que pierre, soit le triple. Combien Pierre a-t-il de billes?
Soit n le nombre de billes de Pierre, il s'agit de résoudre l'équation:
n+6=3n
soit: 6=2n et n=3
Pierre a donc 3 billes (et Pierre en a 9)
ABCD est un carré de 4 cm de côté, E un point du segment [AB].
On pose AE= x
Exprimer l'aire du rectangle EBCF en fonction de x
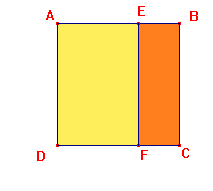
On a :
EB = FC=4-x
d' où l'aire du rectangle EBCF:
a = 4(4-x)=16-4x
La formule :
k(a+b)=ka + kb
nous montre la méthode pour développer un produit qu'il soit littéral ou non:
une nouvelle formule à connaître :
(a+b)(c+d)=ac+ad+bc+bd
(a+b)(c+d)=(a+b)c + (a+b)d (en utilisant une fois la distributivité simple)
(a+b)(c+d)=ac + bc +ad +bd (en l'utilisant deux fois)
Développez l'expression E=(2+3x)+(3-2x)
E=1×(2+3x)+1×(3-2x)
E=1×2+1×3x+1×3+1×(-2x)
E=2+3x+3-2x
On peut enlever des parenthèses si elles sont précédées du signe +
On aurait donc pu écrire de suite:
Développez l'expression E=(2+3x)-(3-2x)
E=1×(2+3x)-1×(3-2x)
E=1×2+1×3x+(-1)×3+(-1)×(-2x)
E=2+3x-3+2x
On peut enlever des parenthèses si elles sont précédées du signe - si on change tous les signes à l'intérieur de cette parenthèse
On aurait donc pu écrire de suite:
etc..
A cette occasion, le test d'une égalité par substitution de valeurs numériques aux lettres prend tout son intérêt. Le travail proposé s'articule autour de trois axes:
La transformation d'une expression littérale s'appuie nécessairement sur la reconnaissance de sa structure (somme, produit) et l'identification des termes ou des facteurs qui y figurent.
L'attention de l'élève sera attirée sur les formes réduites visées du type
ax + b ou ax2 + bx + c.Les situations proposées doivent exclure tout type de virtuosité et répondre à chaque fois à un objectif précis (résolution d'une équation, gestion d'un calcul numérique, établissement d'un résultat général). En particulier, les expressions à plusieurs variables introduites a priori sont évitées.
Les activités de développement prolongent celles qui sont pratiquées en classe de cinquième à partir de l'utilisation de l'identité
k(a + b) = ka + kb.
Le développement de certaines expressions du type
(a + b) (c + d)
peut conduire à des simplifications d'écriture ou de calcul, mais les identités remarquables ne
sont pas au programme.
L'objectif reste de développer pas à pas l'expression puis de réduire l'expression obtenue.
Le Manuel iParcours Maths 4ème reprend le programme officiel 2016 de mathématiques avec cours, activités de découverte et exercices d'entrainement.
Le manuel : 15,95 €