Les conseils de Wouf

Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.

Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.

La meilleure preuve qu'il existe une forme d'intelligence extraterrestre est qu'elle n'a pas essayé de nous contacter.

Pierre Dac - (Sur mon Tshirt!)

Voir toutes les citations.

Triangles et droites parallèles, "petit Thalès" (4ème)

Résumé du cours:

Le petit théorème de Thalès

I. Proportionnalité et équations.

Résoudre les équations suivantes:

II. Triangle en situation de Thalès

Propriété

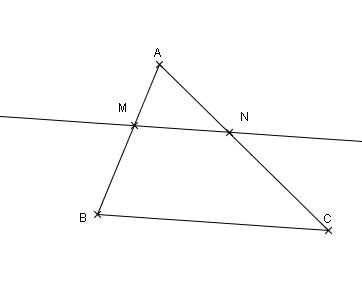
Dans le triangle ABC, M est un point de [B], N est un point de [AC] .

Si (MN)//(BC) Alors :

III. Exemple

Sur la figure suivante, les droites (MP) et (BD) sont parallèles.

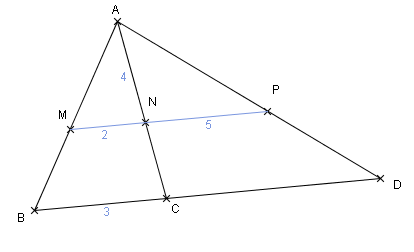
1) Calculer la distance AC. (justifier)

2) Calculer la distance CD. (justifier)

1) Dans le triangle ABC, M appartient au segment [AB] et N appartient au segment [AC].

De plus les droites (MP) et (BD) sont parallèles.

D'après le théorème de Thalès:

Application Numérique:

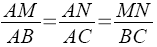
2/3 = 4/AC

AC=12/2=6

2) Dans le triangle ACD, N appartient au segment [AC] et P appartient au segment [AD]. De plus les droites (NP) et (CD) sont parallèles

D'après le théorème de Thalès:

Application Numérique:

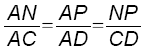
4/6 = 5/CD

CD=30/4 = 7,5

Officiel:

OFFICIEL

CONTENUS

Triangles déterminés par deux droites parallèles coupant deux sécantes.

COMPÉTENCES EXIGIBLES

Connaître et utiliser la proportionnalité des longueurs pour les côtés des deux triangles déterminés par deux droites parallèles coupant deux sécantes :

Dans un triangle ABC, si M est un point du côté [AB], N un point du côté [AC] et si [MN] est parallèle à [BC], alors :

COMMENTAIRES

L'égalité des trois rapports sera admise après d'éventuelles études dans des cas particuliers. Elle s'étend bien sûr au cas où M et N appartiennent respectivement aux demi-droites [AB) et [AC), mais on n'examinera pas le cas où les demi-droites [AM) et [AB), de même que les demi-droites [AN) et [AC), sont opposées.

Le théorème de Thalès dans toute sa généralité ainsi que sa réciproque seront étudiés en classe de 3e.

L'essentiel des notions de mathématiques de la classe de 4ème. Monoposte : 29,00 €

Un manuel de mathématiques de l'association Sésamath pour les classes de 4e (édition 2011). Prix du produit : 11,80 €

Plus de Produits

Liens

Téléchargements:

Cette leçon au format PDF (Adobe Acrobat Reader)

Cette leçon au format Open Office zippée

Tweets by wouf

Comment ???

NEWS

Page : https://site2wouf.fr/petit-thales.php
Catégorie : Mathématiques

Pseudo.py un petit utilitaire pour créer des pseudos

La problématique était la suivante :

L'équipe pédagogiques du collège dans lequel j'exerce désirait, dans le cadre de la semaine des Mathématiques, créer une activité en ligne à destination de toutes les classes de sixième. Chaque élève joue pour sa classe. Il doit donc avoir un pseudo et nous devons, grâce à lui, savoir dans quelle classe il est inscrit.

Or la nécessité d'être en conformité avec le RGPD nous oblige à une certaine prudence.

Notre idée est la suivante :

Nous créons pas classe une liste de 50 pseudos dans lequel un code numérique identifie la classe d'origine. Chaque élève choisit un pseudo et le raye de la liste.

Ce pseudo est son identifiant pour accéder aux activités (via Canopé) . Aucune donnée personnelle n'est sauvegardée...

Pseudo.py

J'utilise un fichier texte avec quelques noms d'animaux :

[text] CHIEN CHAT TAUREAU VACHE AGNEAU CHEVRE CERF LAPIN COCHON CHEVAL LION TIGRE PANTHERE JAGUAR GUEPARD OURS LOUP RENARD HYENE ELEPHANT RHINOCEROS HIPPOPOTAME ZEBRE GIRAFE ANTILOPE KOALA KANGOUROU CASTOR SINGE PANDA LOUTRE TORTUE SERPENT LEZARD IGUANE CROCODILE ALLIGATOR DRAGON PYTHON MOUSTIQUE MOUTON CHEVREUIL OURSON SOURIS RAT POULE CANARD OIE COQ PAON PERROQUET PINGOUIN FLAMANT FOUINE HERISSON COLOMBE PIGEON [/text]

Avec le code python qui suit on génère un fichier texte qui répond au cahier des charges:

[python]from random import * nb_pseudo=50 f = open("animaux.txt", "r") g= open ("result.txt","w") animaux=f.read().splitlines() classes={ "6A": "13,17,21,25,29,33", "6B": "14,18,22,26,34,38", "6C": "11,15,19,23,27,31", "6D": "12,16,24,28,32,36"} for classe in classes.keys(): g.write(classe+"\n") suffixes=(eval(classes[classe])) shuffle(animaux) for n in range(nb_pseudo): g.write(animaux[n]+str(choice(suffixes))+"\n") g.write(40*"-"+"\n") g.close() [/python]

Et on obtient le fichier texte " result.txt ":

[text]6A CHEVRE17 GUEPARD17 OURS29 FOUINE21 POULE13 OURSON17 COLOMBE21 VACHE13 CHEVREUIL21 COQ25 FLAMANT17 COCHON13 HYENE21 CASTOR29 PERROQUET13 KANGOUROU21 GIRAFE29 ANTILOPE33 TORTUE21 TIGRE21 CHIEN17 IGUANE29 TAUREAU17 CHEVAL25 ALLIGATOR25 RENARD25 LION17 PINGOUIN21 PIGEON21 RHINOCEROS21 CHAT13 SERPENT33 MOUTON21 HERISSON21 KOALA29 MOUSTIQUE13 DRAGON25 ZEBRE17 PAON21 SOURIS25 AGNEAU33 PANTHERE33 CROCODILE33 RAT25 PANDA29 SINGE17 LEZARD29 LOUP25 OIE13 CANARD33 ---------------------------------------- 6B PANDA38 RENARD38 CHEVREUIL26 CHAT22 CHIEN22 CHEVRE14 OURSON34 HYENE18 CERF38 PYTHON14 LOUTRE22 VACHE34 HIPPOPOTAME22 CASTOR18 MOUSTIQUE14 LOUP26 FOUINE26 OURS26 LEZARD34 COCHON38 OIE38 SOURIS22 CROCODILE26 SERPENT14 TIGRE26 DRAGON22 IGUANE34 AGNEAU18 PINGOUIN26 SINGE26 ANTILOPE22 ZEBRE14 KANGOUROU14 ALLIGATOR18 HERISSON34 LAPIN22 PERROQUET18 PAON14 COLOMBE26 POULE26 MOUTON38 COQ14 JAGUAR34 ELEPHANT18 LION18 RHINOCEROS14 TAUREAU34 GUEPARD26 FLAMANT26 PANTHERE38 ---------------------------------------- 6C COCHON27 CROCODILE31 ZEBRE11 LOUTRE31 FOUINE19 KANGOUROU23 LEZARD19 GUEPARD11 LAPIN31 PYTHON19 TIGRE19 OIE31 GIRAFE15 COQ31 CHEVAL27 CASTOR19 ELEPHANT15 OURSON15 RENARD19 DRAGON11 TORTUE27 ALLIGATOR11 HYENE31 CHAT31 KOALA15 RHINOCEROS31 LION19 FLAMANT19 PAON23 LOUP15 HIPPOPOTAME11 CERF11 CHEVREUIL11 VACHE19 CHIEN23 SINGE23 AGNEAU27 CHEVRE11 OURS31 IGUANE27 PANTHERE23 SERPENT23 TAUREAU23 POULE31 CANARD23 COLOMBE11 PIGEON23 RAT23 PINGOUIN19 PANDA27 ---------------------------------------- 6D CHEVRE28 PAON32 ZEBRE12 CASTOR16 MOUSTIQUE32 LOUTRE12 CHEVAL36 RENARD24 OURSON36 CHEVREUIL32 ANTILOPE36 TORTUE36 SINGE16 TIGRE12 TAUREAU16 COCHON28 LEZARD24 AGNEAU12 PIGEON28 JAGUAR12 HYENE36 HERISSON36 FLAMANT32 CHAT24 RAT16 PERROQUET28 VACHE16 GIRAFE24 ELEPHANT12 PINGOUIN36 SERPENT24 MOUTON16 POULE28 OURS24 PYTHON24 HIPPOPOTAME28 COLOMBE32 LION12 ALLIGATOR24 GUEPARD12 RHINOCEROS24 COQ16 OIE24 SOURIS12 LOUP16 CERF32 CROCODILE32 PANDA24 KOALA12 FOUINE24 ---------------------------------------- [/text]

Remarques

J'ai choisi les nombres de deux chiffres pour qu'on puisse rapidement retrouver la classe en question : Le reste dans la division euclidienne de ce nombre par 4 donne le rang de la classe :

13 = 4 × 3 + 1 : première classe

Le code Python n'est pas commenté, il est très simple !

lien vers l'article sur wouf blog