Les conseils de Wouf

Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.

Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.

La seule différence entre un ouvrier qui travaille à la mine et un musicien de jazz, c'est que le musicien n'a pas de lampe frontale.

Daniel Humair. (sur Mon tshirt!)

Voir toutes les citations.

Le théorème de Pythagore, en quatrième

Résumé du cours:

Le théorème de Pythagore

I- Comment calculer la longueur d'un côté dans un triangle rectangle ?

A Définition

Dans un triangle rectangle, on appelle hypoténuse le plus grand côté. C'est aussi le côté opposé à l'angle droit.

B Théorème de Pythagore

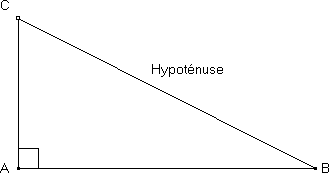
Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des côtés de l'angle droit.

Dans le triangle ABC rectangle en A : BC²= AB² + AC²

C Exemples :

1. Soit RFA un triangle rectangle en F, RF=3 cm et FA=4 cm.

Calculer RA.

Dans le triangle RFA rectangle en F, d'après le théorème de Pythagore :

RA²=RF²+FA² donc

RA²=3²+4²= 9+16= 25

d'où RA=5 cm

2. Dans le triangle PIF rectangle en I, PI=4 cm et PF=7 cm.

Calculer IF.

Dans le triangle PFI rectangle en I, d'après le théorème de Pythagore :

PF²= PI² + IF² donc 72 = 42 + IF² donc IF²= 49 - 16 = 33

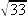
d'où IF = Racine(33) environ 5,7 cm

II- Comment démontrer qu'un triangle est rectangle ?

A Réciproque du théorème de Pythagore :

Si dans un triangle le carré d'un côté est égal à la somme des carrés des autres côtés alors ce triangle est rectangle.

C'est à dire :

Dans le triangle AZE si AZ² = ZE² + AE²

alors AZE est un triangle rectangle en E (AZ est l'hypoténuse)

B. Exemple :

Soit HTJ tel que HT=12 cm, HJ=13 cm, JT=5cm.

Quelle la nature de ce triangle ?

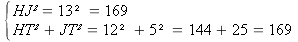
donc HJ² = HT² + JT²

D'après la réciproque du théorème de Pythagore, le triangle HTJ est rectangle en T

III- Comment démontrer qu'un triangle n'est pas rectangle ?

A Exemple :

Soit ERT tel que ER=5 cm, RT=4cm, TE=6cm.

Le triangle est-il rectangle ?

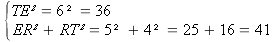
Donc TE² 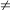different ER² + RT² Le triangle ERT n'est pas rectangle.

B Remarque :

Si le triangle ERT était rectangle alors l'égalité TE² = ER² + RT² serait vraie d'après le théorème direct de Pythagore.

Officiel:

Compétences exigibles :

Caractériser le triangle rectangle :

par son inscription dans un demi-cercle
par la propriété de Pythagore et sa réciproque.

Calculer la longueur d'un côté d'un triangle rectangle à partir de celles des deux autres.

En donner, s'il y a lieu, une valeur approchée, en faisant éventuellement usage de la touche racine d'une calculatrice.

Trouver à l'aide de la calculatrice une valeur approchée de la racine carrée d'un nombre positif.

Commentaires :

On poursuit le travail sur la caractérisation des figures en veillant à toujours la formuler à l'aide d'énoncés séparés.

Les relations métriques dans le triangle rectangle, autres que celles mentionnées dans les compétences exigibles, ne sont pas au programme.Le théorème de Pythagore fournit l'occasion de calculer des racines carrées de nombres positifs dans des cas qui relèvent d'une situation où le nombre calculé a une signification que l'élève peut identifier.

On peut aussi rattacher le calcul d'une racine carrée à des problèmes où interviennent l'aire d'un carré et la mesure de son côté.

L'essentiel des notions de mathématiques de la classe de 4ème. Monoposte : 29,00 €