L'expérience est le nom que chacun donne à ses erreurs.
Oscar Wilde (sur mon T shirt!)
Dans cette leçon, nous allons explorer différents types de solides géométriques. Nous verrons leurs définitions, leurs patrons et leurs perspectives cavalières.
Un solide géométrique est un objet en trois dimensions, comme un cube ou une pyramide. Chaque solide a des faces, des arêtes et des sommets.
Un patron est une figure plane qui permet de construire un solide en pliant du papier. Il est constitué de toutes les faces du solide disposées à plat.
La perspective cavalière est une méthode de dessin qui permet de représenter un objet en trois dimensions sur une surface plane. Elle montre comment les faces d'un solide sont reliées entre elles.
En perspective cavalière, les parallèles dans la réalité sont représentées par des droites parallèles.
Par convention, on représente les arêtes invisibles en pointillés.
En majorité, le pavé autobloquant est un pavé en béton. Il est composé de gravier, de sable, de ciment et d’eau. Il a la forme d'un pavé droit.
Un pavé droit (ou parallélépipède rectangle) est un solide ayant six faces rectangulaires. Ses arêtes sont perpendiculaires à ses bases.
Le patron d'un pavé droit est constitué de six rectangles disposés de manière à pouvoir être pliés pour former le solide.
Dans le cahier d'exercices, dessine le patron d'un pavé droit dont les dimensions sont 3cm, 4cm et 5cm.
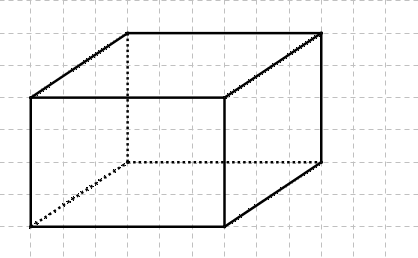
La perspective cavalière permet de représenter le pavé droit en trois dimensions sur une surface plane.
Cet organisateur de bureau à la forme d'un prisme droit à base triangulaire.
Un prisme droit est un solide dont les deux bases sont des polygones parallèles et superposables, et dont les faces latérales sont des rectangles.
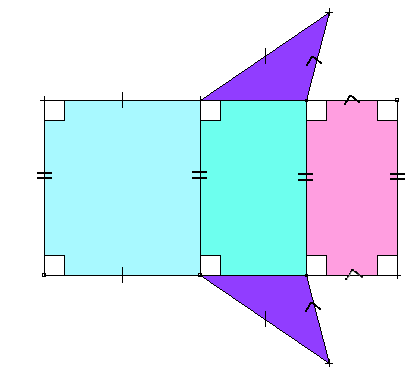
Le patron d'un prisme droit comprend deux polygones pour les bases et des rectangles pour les faces latérales.
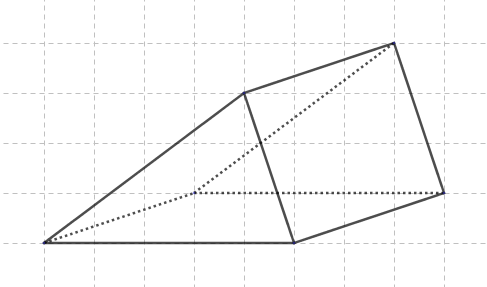
Un cylindre est un solide ayant deux bases circulaires parallèles, reliées par une surface courbe. La distance entre les deux centres des bases est appelée la hauteur du cylindre.
Le patron d'un cylindre comprend deux cercles pour les bases et un rectangle pour la surface latérale.
Une pyramide est un solide ayant une base polygonale et des faces triangulaires qui se rejoignent en un sommet.
Le patron d'une pyramide comprend un polygone pour la base et des triangles pour les faces latérales.
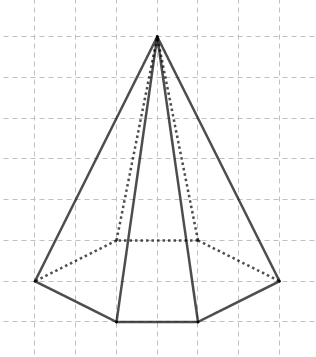
Ci-dessus, la reproduction en perspective cavalière d'une pyramide à base hexagonale.
Un cône de révolution est un solide ayant une base circulaire et une surface courbe qui se termine en un sommet unique.
Le patron d'un cône est composé d'un disque pour la base et d'un secteur circulaire pour la surface latérale.
La sphère est la surface formée par l'ensemble des points situés à une distance fixe d'un point appelé le centre. La boule est l'espace contenu à l'intérieur de cette surface.
Une sphère, comme une boule est représentée en perspective cavalière par un cercle.
Les solides géométriques sont un élément clé de l'enseignement des mathématiques aux cycles 3 et 4. Cette leçon s'inscrit dans le cadre des instructions officielles du Ministère de l'Éducation nationale, permettant aux élèves de développer des compétences essentielles en géométrie dans l'espace.
« Comprendre et utiliser les propriétés des solides usuels (pavé droit, prisme, cylindre, cône, sphère, etc.). Identifier leurs représentations : patrons, perspectives cavalières et modélisations numériques. »
Source : Programmes de Mathématiques, Cycle 3 et Cycle 4
Cette leçon peut être enrichie avec des activités concrètes : création de patrons, modélisation avec des logiciels de géométrie dans l'espace, ou encore la manipulation de solides en papier ou en carton. Ces approches permettent aux élèves de mieux comprendre les concepts abstraits liés aux solides géométriques.
Pour plus de ressources pédagogiques, consultez le site officiel : Eduscol.
