Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
C'est de ta peur que j'ai peur.
| km³ | hm³ | dam³ | m³ | dm³ | cm³ | mm³ | ||||||||||||||
| kL | hL | daL | L | dL | cL | mL | ||||||||||||||
| 3 | 2 | 1 | ||||||||||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||||||
La deuxième ligne est constituée des unités de contenance :
On a 1 L = 1 dm³
A l'aide du tableau on peut observer qu'une marmite qui peut contenir 3 210 cm³ d'eau a une contenance de 3,21 L ou qu'un volume d'un km³ est égal à un volume de 1 000 000 000 m³, soit un milliard de m³.
Dans cette section, nous découvrons deux solides courants : le prisme droit et le cylindre. Nous apprendrons à les reconnaître, les représenter et calculer leurs caractéristiques géométriques.
Un prisme droit est un solide qui a :
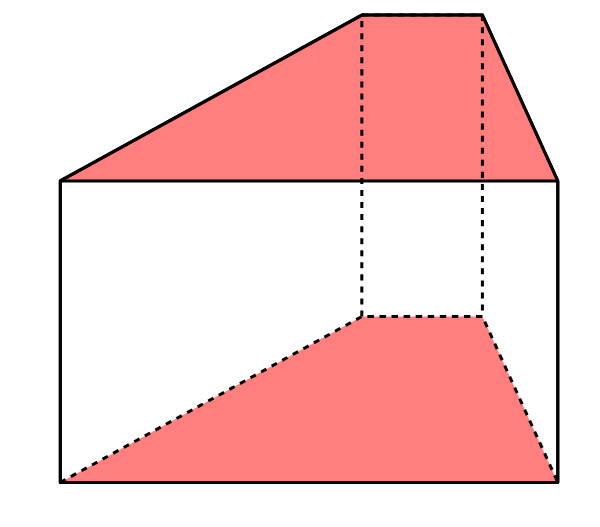
Le prisme ci-dessus est un prisme à bases quadrilatères. Les deux bases sont colorées. Les arêtes invisibles sont dessinées en pointillés.
L'image ci-dessus est une représentation en perspective cavalière.
La perspective cavalière est un outil précieux pour représenter des objets en trois dimensions sur une surface plane. Elle permet de donner une idée précise de la forme et des proportions d'un objet, tout en conservant la simplicité des parallèles.
Le patron est un dessin plat d'un objet en 3D qu'on peut plier pour reconstituer l'objet.
Voici un patron codé représentant ce prisme : chaque face y est clairement identifiée pour faciliter la reconstruction.
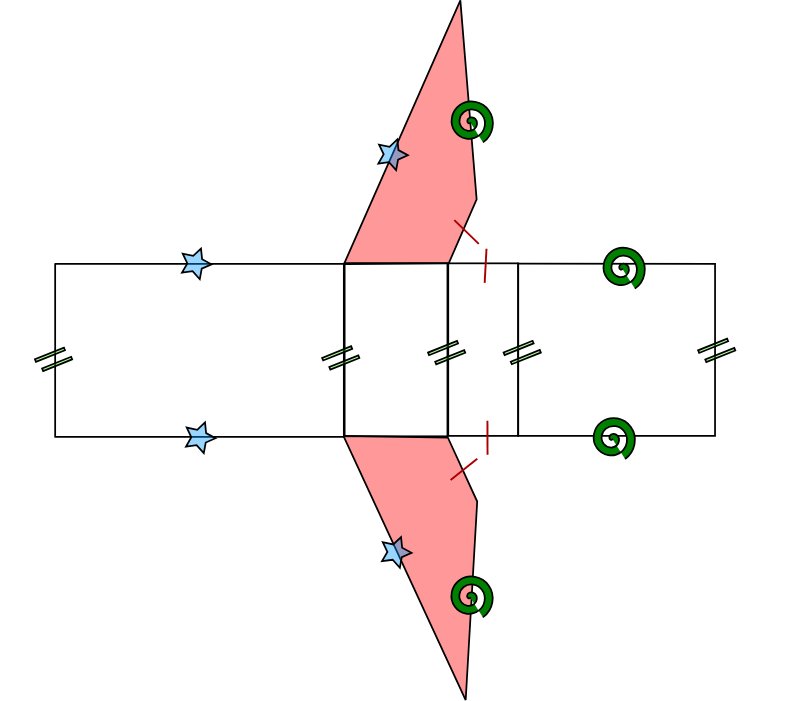
On appelle aire latérale d'un prisme droit l'aire de toutes les faces sauf les bases.
Pour calculer l'aire latérale d'un prisme droit, on multiplie le périmètre d'une base (quadrilatère rouge) par la hauteur du solide (côtés codés par les deux traits verts.)
On ajoute alors deux fois l’aire de la base pour obtenir l’aire totale.
Pour calculer le volume d'un prisme droit, on multiplie cette fois l'aire d'une base par la hauteur du solide.
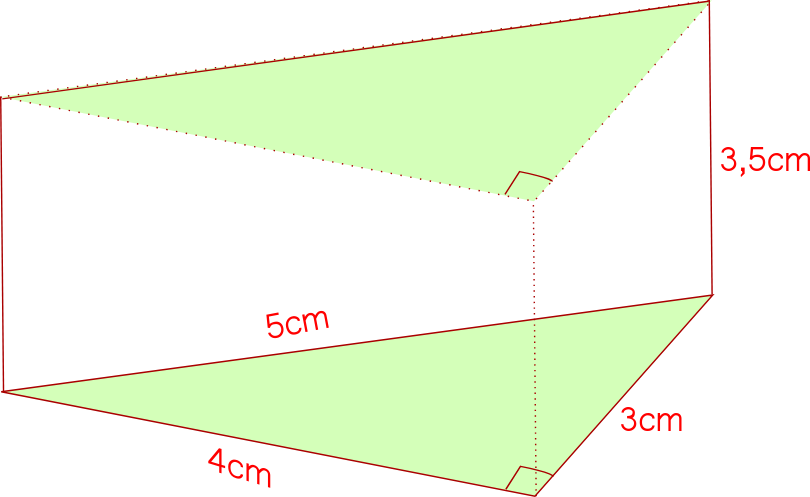
Dans le cahier d'exercices :
Un cylindre de révolution est un solide qui a :
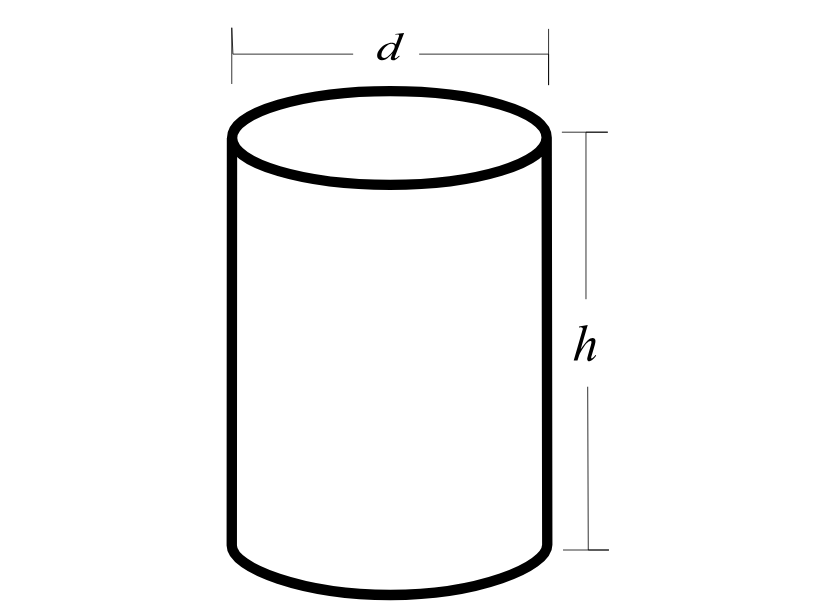
La distance entre les deux bases (h) est appelée hauteur du cylindre.
Le patron est constitué d'un rectangle et de deux disques.
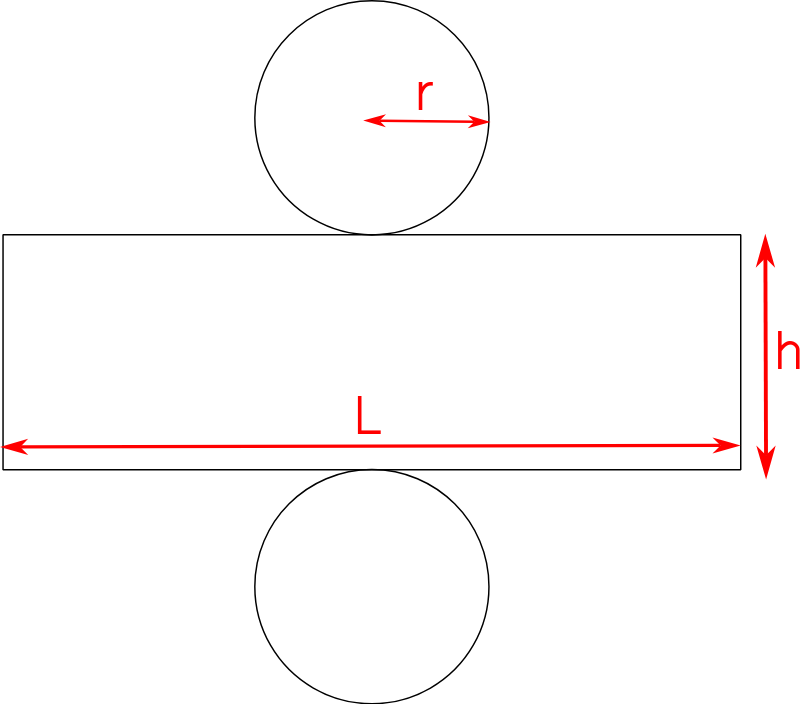
Avec L = 2 × π × r
En effet ce côté du rectangle vient "se coller" sur le tour du disque donc sa longueur est égale au périmètre du cercle.
On appelle aire latérale d'un cylindre de révolution l'aire de toutes les faces sauf les bases.
Il s'agit de l'aire du rectangle dans le patron ci-dessus, c'est à dire
L × h = 2 × π × r × h
Il suffit d'ajouter le double de l'aire du disque de base :
L'aire totale est :
2 × π × r × h + 2 × π × r2
Comme pour le prisme droit pour calculer le volume d'un cylindre de révolution il suffit de multiplier l'aire de la base par la hauteur :
V = π × r2 × h
Cette leçon s’inscrit dans le cadre du programme de mathématiques du cycle 4, plus précisément dans le domaine "Espace et géométrie". En classe de 5e, les élèves doivent être capables de reconnaître et représenter des solides usuels, notamment les prismes droits et les cylindres, d’en construire des patrons, et de calculer leurs aires et volumes.
Les attendus de fin de cycle précisent que les élèves doivent : "reconnaître et nommer des solides usuels", "représenter des solides et leurs patrons", "calculer des volumes et des aires de solides simples", et "mobiliser les propriétés géométriques dans des situations variées". Ces attendus sont détaillés dans le document d'accompagnement du programme.
Cette leçon mobilise plusieurs compétences du socle commun de connaissances, de compétences et de culture, notamment :
Elle peut être enrichie par des activités complémentaires proposées dans les ressources mathématiques du collège sur Éduscol, comme des manipulations de patrons, des représentations dynamiques ou des exercices contextualisés en lien avec les sciences et la technologie.
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: