
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Je connais mes limites. C'est pourquoi je vais au-delà.
Serge Gainsbourg (sur mon T shirt!)




Résoudre les équations suivantes:
x 2 = 5 6
5 3 = x 6
11 3 = 22 x
6 x = 15 2
x 2 = 13
3 x = 5

x = 5 × 2 6 = 10 6 = 5 3
x = 5 × 6 3 = 30 3 = 10
x = 3 × 22 11 = 66 11 = 6
x = 6 × 2 15 = 12 15 = 4 5 = 0,8
x = 13 × 2 1 = 26
x = 3 × 1 5 = 3 5 = 0,6

Soient (d) et (d') deux droites sécantes en A. Soient B et M deux points de d (distincts de A). Soient C et N deux points de (d') (distincts de A).
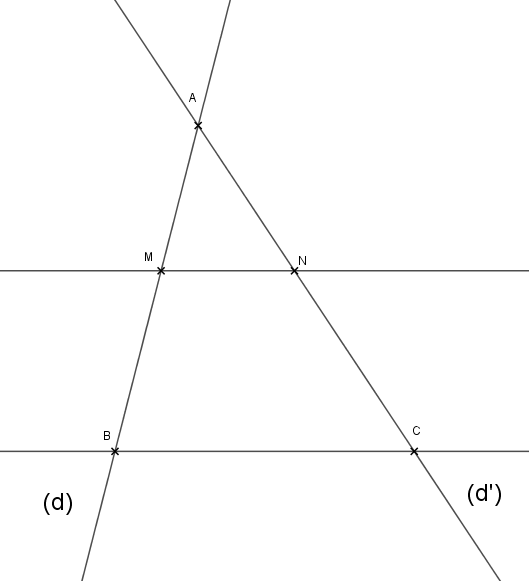
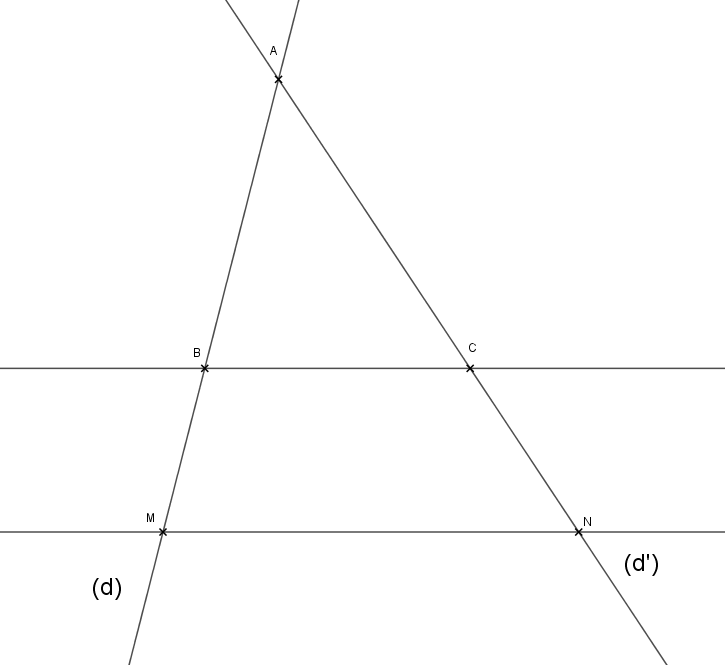
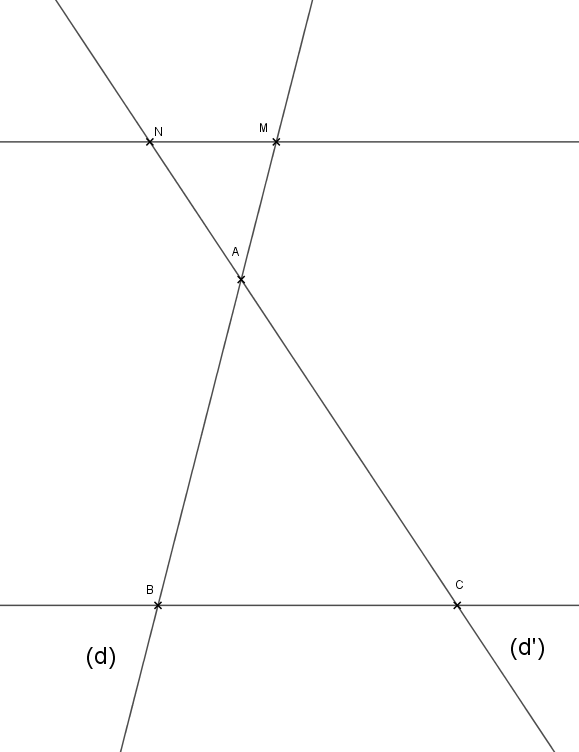
On peut imaginer que les points A,B et C sont fixes et que la droite (MN) se déplace, M restant sur (d) et N sur (d').
On comprendra, en poursuivant, pourquoi il semble que (MN) et (BC) sont paralléles dans ces trois figures clés...
Soient (d) et (d') deux droites sécantes en A. Soient B et M deux points de (d) distincts de A. Soient C et N deux points de (d') distincts de A. Si les droites (BC) et (MN) sont parallèles alors:
AM AB = AN AC = MN BC
1) Construire un triangle ABC ayant pour dimensions :
AB = 7 cm ; AC = 4 cm ; BC = 5 cm.
2) Soit M le point situé sur le segment [AB] et tel que AM = 1 cm. La parallèle à la droite (AC) passant par M coupe la droite (BC) en N.
Calculer BN et MN.
(Donner les résultats d'abord sous forme fractionnaire, et ensuite sous forme décimale arrondie à 0,1 près.)

On commence par tracer le plus grand côté [AB].
Le point C est à l'intersection du cercle de centre A et de rayon 4 cm, et du cercle de centre B et de rayon 5 cm.
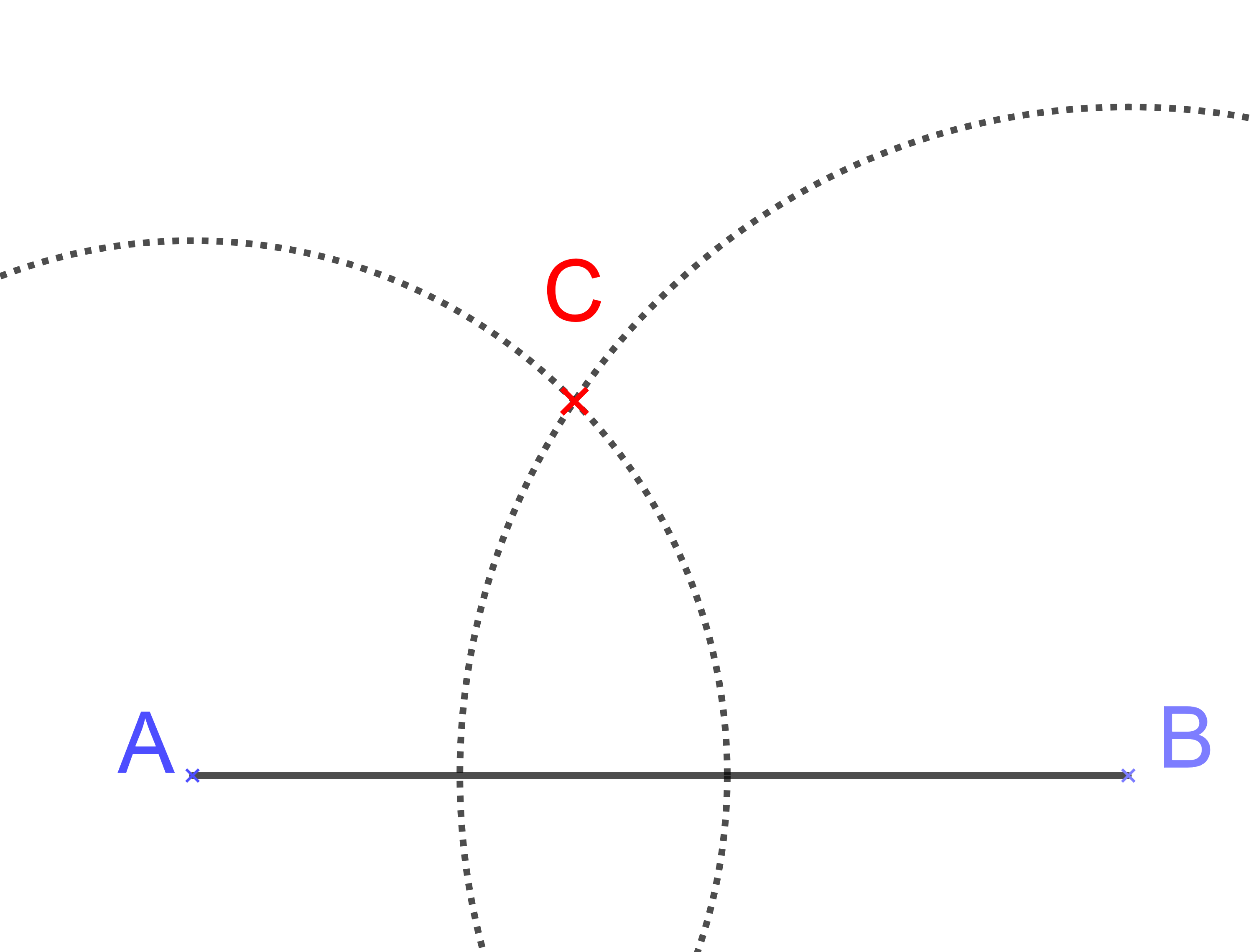
Il y a deux intersections entre les cercles, on en choisit une !
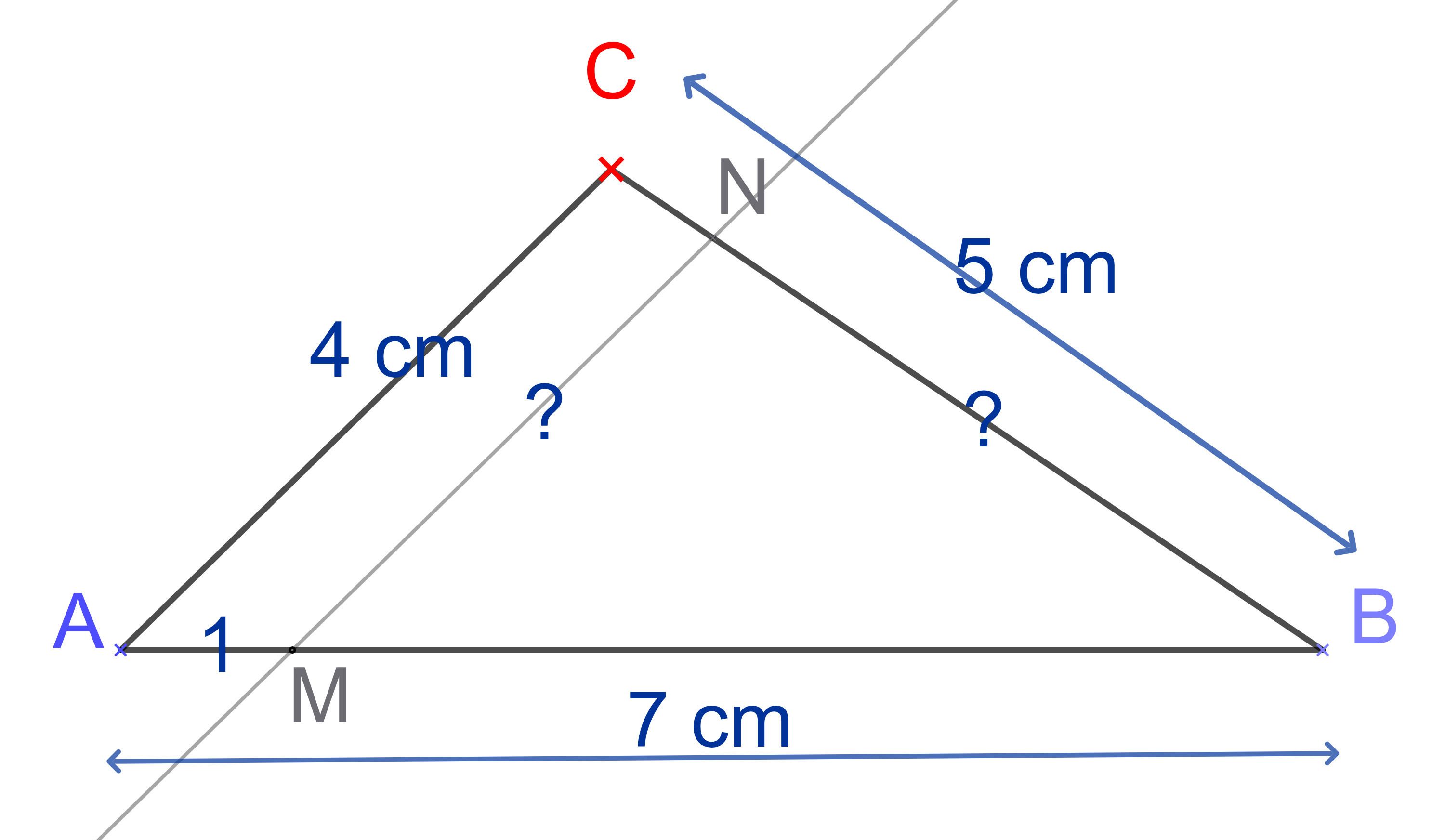
Remarquez qu'en le disant comme ça, on cite les 5 points de la figure clef !
D'après le théorème de Thalès :
BN BC = BM BA = NM CA
BN 5 = 7-1 7 = NM 4
BN 5 = 6 7 = NM 4
D'où :
BN = 6 × 5 7 = 30 7 ≈ 4,3 cm
NM = 6 × 4 7 = 24 7 ≈ 3,4 cm
Domaine : Espace et géométrie
Domaine : Grandeurs et mesures

Dans les deux premières figures clés(celles connues depuis la quatrième) on peut observer un "petit" triangle et un "grand" triangle.
Toutes les longueurs du grand triangle peuvent être obtenues en multipliant celles du petit triangle par un même coefficient k (k>1) appelé coefficient d'agrandissement.
Toutes les longueurs du petit triangle peuvent être obtenues en multipliant celles du grand triangle par un même coefficient k (0<k<1) appelé coefficient de réduction.
Démontrer que:
3+7 5 = 18 9
La méthode classique pour démontrer une égalité consiste à partir d'un des membres et d'arriver à l'autre par une suite de calculs:
3+7 5 = 10 5 = 2 = 18 9
On peut aussi s'occuper indépendamment des deux membres et espérer arriver au même résultat:
3+7 5 = 10 5 = 2
18 9 = 2
Donc :
3+7 5 = 18 9
Soient (d) et (d') deux droites sécantes en A. Soient B et M deux points de (d) distincts de A. Soient C et N deux points de (d') distincts de A. Si AM AB = AN AC et si les points A,B,M et les points A,C,N sont dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Soit un triangle PIF tel que PI = 5 cm ; PF = 6 cm ; IF = 8 cm. L est un point du segment [PI] tel que IL = 2 cm et A un point du segment [PF] tel que PA = 3,6 cm.

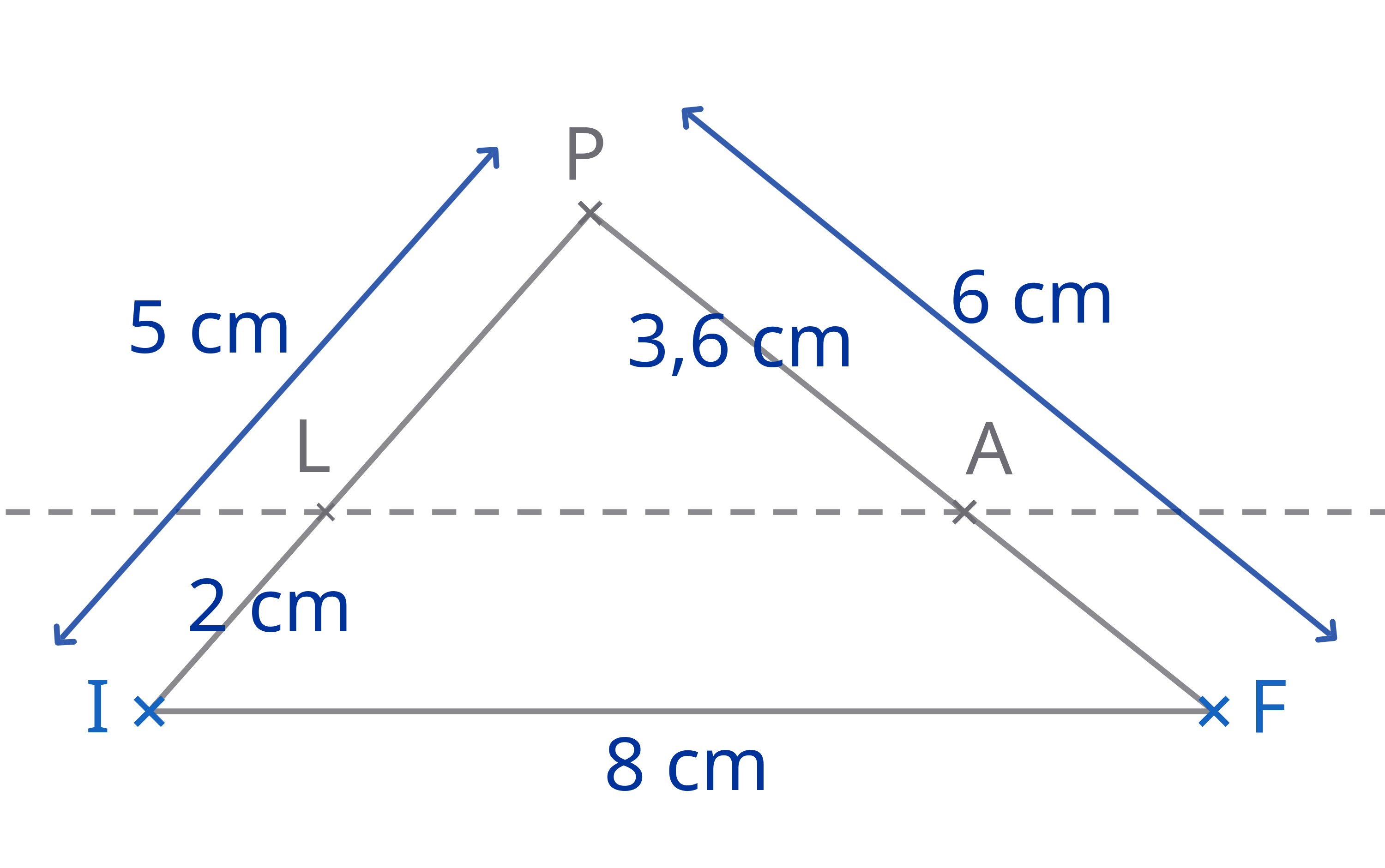
PL = PI - IL = 5 - 2 = 3 cm
PL PI = 3 5
PA PF = 3,6 6 = 36 60 = 6 10 = 3 5
PL PI = PA PF
D'après la réciproque du théorème de Thalès, les droites (LA) et (IF) sont parallèles.
D'après le théorème de Thalès :
PL PI = PA PF = LA IF
LA 8 = 3 5
LA = 3 × 8 5 = 24 5 = 4,8 cm
Domaine : Espace et géométrie
Domaine : Grandeurs et mesures

Connaître et utiliser dans une situation donnée les deux théorèmes suivants :
Soient d et d' deux droites sécantes en A. Soient B et M deux points de d distincts de A. Soient C et N deux points de d' distincts de A. Si les droites (BC) et (MN) sont parallèles alors:

Soient d et d' deux droites sécantes en A. Soient B et M deux points de d distincts de A. Soient C et N deux points de d' distincts de A. Si
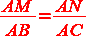
et si les points A,B,M et les points A,C,N sont dans le même ordre, alors les droites (BC) et (MN) sont parallèles.
Il s'agit d'un prolongement de l'étude faite en classe de 4ème. L'étude de la propriété de Thalès est l'occasion de traiter des situations de proportionnalité dans le cadre géométrique du plan et de l'espace. La réciproque est formulée en tenant compte de l'ordre relatif des points sur chaque droite.
L'utilisation d'un logiciel de construction géométrique pour permettre de créer des situations reliées au Théorème de Thalès, notamment lors des activités d'approche de la propriété par la mise en évidence de la conservation des rapports.
Le travail de construction de points définis par des rapports de longueurs permet de mettre en évidence l'importance de la position relative de ces points sur la droite. On s'intéressera particulièrement au problème suivant:
Etant donnés 2 points A et B, construire le point C de la droite (AB) sachant que le rapport a une valeur donnée sous forme de quotient d'entiers.
La réciproque est formulée en tenant compte de l’ordre relatif des points sur chaque droite mais, dans le cadre du socle commun, les élèves n’ont pas à distinguer formellement le théorème direct et sa réciproque. L’utilisation d’un logiciel de construction géométrique permet de créer des situations d’approche ou d’étude du théorème et de sa réciproque.
Le travail demandé en géométrie, qui s'inscrit en complément, au moins partiel, de celui engagé précédemment (sur les configurations, les isométries), généralise des résultats antérieurs (situation de Thalès, angle inscrit...), tout en ouvrant un nouveau champ à la mise en oeuvre de démonstrations;
Dans les démonstrations, les initiatives des élèves sont encouragées. Les propriétés de Thalès et de l'angle inscrit permettent de traiter de nombreux problèmes. Les occasions de lier les domaines géométrique et numérique sont nombreuses ; le travail sur les objets du plan et de l'espace sert de support à des activités de calculs numériques et littéraux ; la manipulation des écritures de quotients permet, par exemple, de démontrer l'alignement des points représentatifs d'une fonction linéaire ou de justifier la construction des points partageant un segment dans un rapport donné sous forme d'un quotient d'entiers.
D'autre part, en exploitant le fait qu'une perpendiculaire à un plan en un point est perpendiculaire à toutes les droites du plan passant par ce point, on démontre, avec le théorème de Pythagore, que les sections planes d'une sphère sont des cercles. De même, on démontre, en utilisant de plus la propriété de Thalès, que la section d'une pyramide par un plan parallèle à sa base est une réduction de cette base.
Les problèmes d'orientation de la droite rencontrés également dans l'étude des situations de Thalès seront traités ultérieurement à d'autres niveaux avec l'homothétie et le produit d'un vecteur par un réel.
Ils ont rencontré et ont eu l'occasion d'élaborer, au cours de démonstrations, différents types de raisonnement : raisonnement déductif, raisonnement par disjonction des cas lors de l'examen de l'effet de la multiplication sur l'ordre, infirmation par mise en évidence d'un contre-exemple, approche du raisonnement par l'absurde lorsqu'il s'agit de reconnaître si une configuration est une configuration de Thalès ou si un triangle est rectangle.

Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager :