Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Dieu a dit : "Tu aimeras ton prochain comme toi-même." D'abord, Dieu ou pas, j'ai horreur qu'on me tutoie...
Pierre Desproges (sur mon T shirt!)
On appelle parallélogramme un quadrilatère dont les côtés opposés sont parallèles.
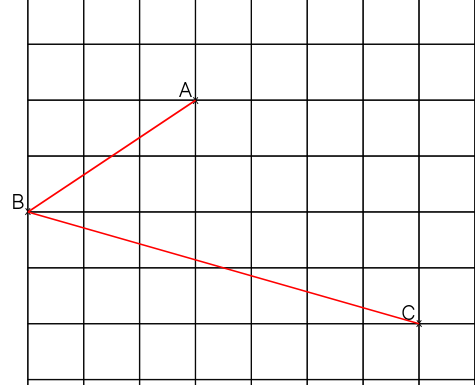
Soient A, B et C trois points alignés comme dans la figure suivante :
On commence par tracer les côtés [AB] et [BC] :
Dans un parallélogramme les côtés opposés sont parallèles et de même longueur.
Cette propriété admet également une réciproque :
Dans un quadrilatère non croisé, si deux côtés sont parallèles et de même longueur alors ce quadrilatère est un parallélogramme.
Pour passer de B à C on se déplace de 7 carreaux vers la droite et on descend de deux carreaux. On reproduit ces déplacements à partir de A :
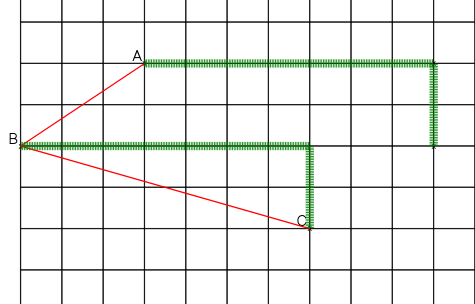
On obtient bien un quadrilatère ABCD non croisé, tel que (BC)//(AD) et BC = AD : Le parallélogramme ABCD
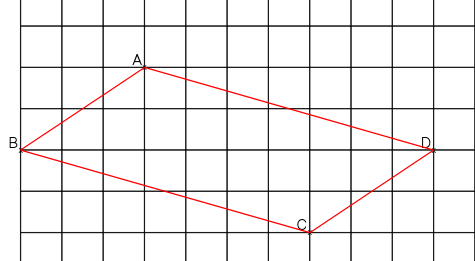
Dans un parallélogramme les diagonales se coupent en leur milieu.
Cette propriété admet également une réciproque :
Un quadrilatère dont les diagonales se coupent en leur milieu est un parallélogramme.
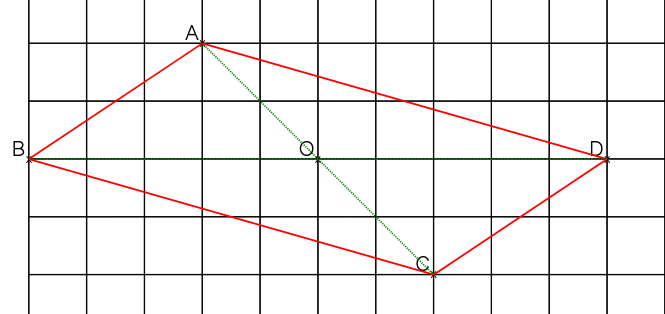
On commence donc par tracer la diagonale [AC] puis on place son milieu O
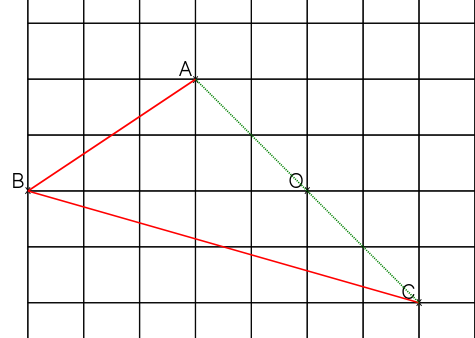
Et on place D, tel que O soit le milieu de [BD]. Ainsi, ABCD est un quadrilatère dont les diagonales se coupent en leur milieu, c'est bien un parallélogramme.
Il existe de nombreuses méthodes pour tracer un parallélogramme connaissant trois de ses sommets , par exemple :
Ces 3 façons de travailler seront vues en activité.
C'est en réfléchissant à ce qu'on sait par l'énoncé et aux propriétés caractéristiques qu'on trouvera la méthode la plus intéressante !
Dans le rectangle, le losange et le carré qui sont des parallélogrammes particuliers, les propriétés du parallélogramme sont toujours d'actualité. Ainsi les côtés opposés sont parallèles et de même longueur et les diagonales ont même milieu !
Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.
Dans le cahier d’exercices dessine un rectangle RECT de centre A tel que RC = 5 cm et RE = 2 cm.
Si un parallélogramme a ses diagonales perpendiculaires alors c'est un losange.
Dans le cahier d’exercices dessine un losange ANGE dont les diagonales mesurent 6cm et 5cm.
Si un parallélogramme a ses diagonales de même longueur et perpendiculaires alors c'est un carré.
Dans le cahier d’exercices dessine un carré dont les diagonales mesurent 4 cm.
Les problèmes de construction constituent un champ privilégié de l’activité géométrique tout au long du cycle 4. Ces problèmes, diversifiés dans leur nature et la connexion qu’ils entretiennent avec différents champs mathématiques, scientifiques, technologiques ou artistiques, sont abordés avec les instruments de tracé et de mesure. Dans la continuité du cycle 3, les élèves se familiarisent avec les fonctionnalités d’un logiciel de géométrie dynamique ou de programmation pour construire des figures.
La pratique des figures usuelles et de leurs propriétés, entamée au cycle 3, est poursuivie et enrichie dès le début et tout au long du cycle 4, permettant aux élèves de s’entraîner au raisonnement et de s’initier petit à petit à la démonstration
La symétrie axiale a été introduite au cycle 3. La symétrie centrale est travaillée dès le début du cycle 4, en liaison avec le parallélogramme.
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: