
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Les iguanes c'est ultra bizarre.
Vincent Delerm


a étant un nombre relatif, on appelle carré de a, le nombre noté a2 tel que :
a2 = aa
a étant un nombre relatif, on appelle cube de a, le nombre noté a3 tel que:
a3 = aaa
23=8
(-3)3=-27
a étant un nombre relatif et n un entier relatif n>1:
an = aaa........aaa avec n fois le facteur a
On lit a puissance n, n est l'exposant.
Un nombre non nul, élevé à la puissance 0 est égal à 1 :
x0=1
Un nombre élevé à la puissance 1 est égal à lui même :
x1=x
On généralise pour les entiers relatifs:
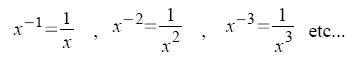
Au passage, on comprend la notation de l'inverse sur certaine calculatrice.
La puissance est prioritaire sur les autres opérations.
Ne pas confondre :
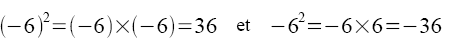
Pour calculer avec des puissances, il est nécessaire de bien connaître la définition et d'y revenir aussi souvent que possible!
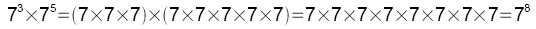
En revenant à la définition, on s'aperçoit qu'il suffit d'ajouter les exposants!
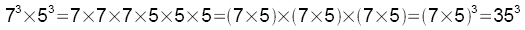
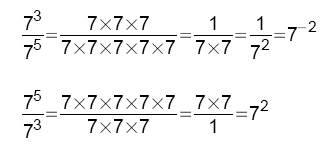
En revenant à la définition, on s'aperçoit qu'il suffit de soustraire les exposants!
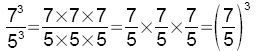
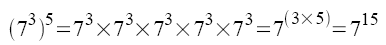
En revenant à la définition, on s'aperçoit qu'il suffit de multiplier les exposants!
103 = 1 000 (exposant +3 et 3 zéros après le 1)
10-5 = 0,00001 (exposant -5 et 5 zéros avant le 1)
Si n est un entier positif :
10n est un nombre entier qui s'écrit avec un 1 suivi de n zéro(s)
10-n est un nombre décimal qui s'écrit 0,00..001 ,il y a n zéros avant le 1.
L'écriture scientifique d'un nombre est de la forme a x 10n où a est un nombre décimal tel que:
Donner l'écriture scientifique des nombres suivants:
789 = 7,89 x 10 2
0,0258 = 2,58 x 10 -2
L' écriture scientifique d'un nombre permet d'avoir très rapidement une idée de l'ordre de grandeur d'un nombre.
156 000 000 000 000 000 000 est beaucoup moins parlant que 1,56 x 1020
(pour le comparer avec un autre grand nombre par exemple)
Comprendre les notations et et savoir les utiliser sur des exemples numériques pour des exposants très simples et pour des égalités telles que:
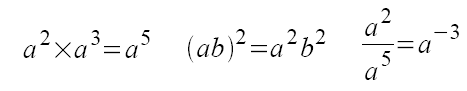
où a et b sont des nombres relatifs non nuls.
Utiliser sur des exemples numériques, les égalités :
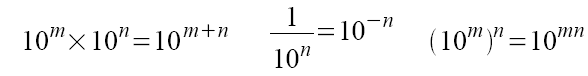
où m et n sont des entiers relatifs.
Cette rubrique ne doit pas donner lieu à des calculs artificiels sur les puissances entières d'un nombre relatif, Pour des nombres autres que 10, seuls des exposants simples sont utilisés.
Les résultats sont obtenus en s'appuyant sur la signification de la notation puissance et non par l'application des formules.
En liaison avec les sciences expérimentales, en particulier avec la physique, qui abordent le domaine microscopique d'une part, l'échelle astronomique d'autre part, les activités insistent sur l'usage des puissances de 10.
A cet effet, les élèves utilisent largement la calculatrice, dont ils doivent maîtriser l'utilisation des touches correspondantes.

Le Manuel iParcours Maths 4ème reprend le programme officiel 2016 de mathématiques avec cours, activités de découverte et exercices d'entrainement.
Le manuel : 15,95 €