Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Le plus beau compliment que je puisse faire à une femme est de lui dire : je suis aussi bien avec toi que si j'étais tout seul.
Jean Yanne
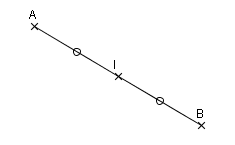
Soit un segment [AB] et son milieu I, on dit que A et B sont symétriques par rapport à I.
Les points M et M' sont symétriques par rapport à un point V.
Tracer le symétrique de A par rapport à I
On commence par tracer la demi-droite [AI) que l'on prolonge suffisamment.
Le cercle de centre I et de rayon AI recoupe le demi droite [AI) en A'.
On n'oublie pas de coder!
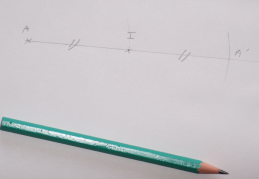
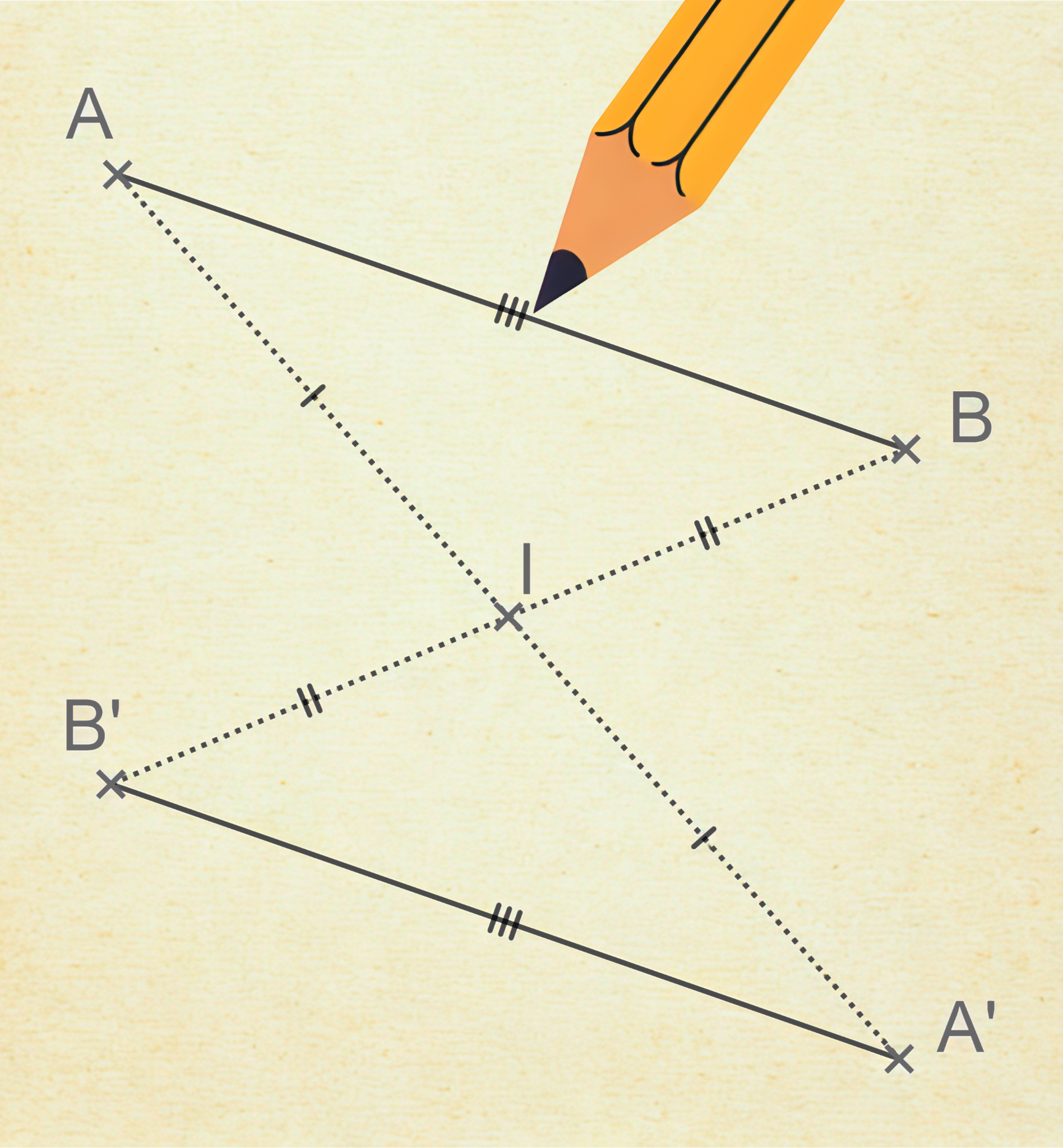
L'image d'un segment par une symétrie centrale est un segment de même longueur.
Pour construire le symétrique du segment [AB] par la symétrie centrale de centre O il suffit de tracer le segment [A'B'] où A' et B' sont respectivement les symétriques de A et B.
L'image d'une droite par une symétrie centrale est une droite parallèle.
Pour construire le symétrique de la droite (AB) par la symétrie centrale de centre O il suffit de tracer la droite (A'B') où A' et B' sont respectivement les symétriques de A et B.
La symétrie centrale conserve les longueurs.
Autrement dit :
L'image d'un segment par une symétrie centrale est un segment de même longueur.
La symétrie centrale conserve la mesure des angles.
Autrement dit :
L'image d'un angle par une symétrie centrale est un angle égal.
La symétrie centrale conserve les périmètres.
La symétrie centrale conserve les aires.
Comme en classe de sixième, un travail expérimental permet d’obtenir un inventaire abondant de figures simples. Les propriétés invariantes dans une symétrie centrale sont ainsi progressivement dégagées et comparées avec les propriétés invariantes dans une symétrie axiale.
la construction de l’image d’une figure simple, l’énoncé et l’utilisation de propriétés caractéristiques du parallélogramme ; la caractérisation angulaire du parallélisme et son utilisation ; la justification de formules relatives aux aires.
La symétrie centrale n’a, à aucun moment,à être présentée comme application du plan dans lui-même.
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: