Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Une erreur originale vaut mieux qu'une vérité banale.
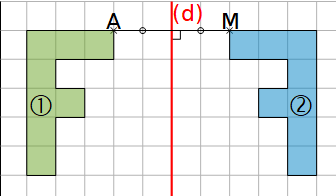
Deux figures sont symétriques par rapport à une droite si elles se superposent par pliage le long de cette droite. Cette droite est appelée l'axe de symétrie.
copyright de l'image : sesamath.net
Les figures 1 et 2 se superposent par pliage sur la droite (d). On dit qu'elles sont symétriques par rapport à la droite (d).
On dit aussi que la figure 2 est le symétrique de la figure 1 dans la symétrie axiale d'axe (d).
Deux points sont symétriques par rapport à une droite s'ils se superposent par pliage le long de cette droite.
Ici, les points A et M sont symétriques par rapport à la droite (d).
On dit aussi que M est le symétrique de A dans la symétrie axiale d'axe (d) (ou que A est le symétrique de M...)
Le symétrique d'un point A par rapport à une droite (d) est le point B tel que la droite (d) soit la médiatrice du segment [AB] (tel que (d) soit la perpendiculaire au segment [AB] en son milieu).
![(d) médiatrice de [AB]](https://site2wouf.fr/coll/l6/symetrie_axiale/d_med_AB.png)
Si un point appartient à une droite alors son symétrique par rapport à cette droite est le point lui-même.
Dans un quadrillage il suffit de savoir compter (voir téléchargements en bas de page, ou exercices).
Hors quadrillage, on dispose de plusieurs types de constructions
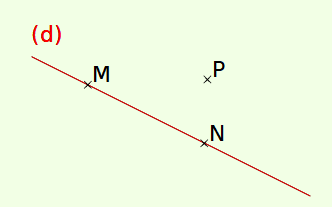
On commence par prendre deux points distincts quelconques M et N sur la droite (d).
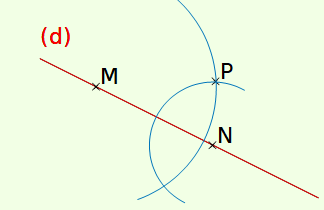
On trace deux arcs de cercle de centres M et N passant par P
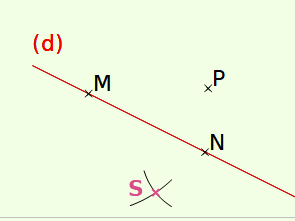
Ces deux arcs se coupent au point S, le symétrique de P par rapport à (d).
La symétrie axiale conserve :
Une droite (d) est un axe de symétrie d’une figure si les deux parties de la figure se superposent par pliage le long de cette droite.
Un segment a deux axes de symétrie : la droite qui contient ce segment et la médiatrice de ce segment.
Si un point appartient à la médiatrice d’un segment, alors il est situé à égale distance des extrémités de ce segment.
Réciproquement, si un point est équidistant des extrémités d’un segment, alors il appartient à la médiatrice de ce segment.
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles de même mesure.
La bissectrice d'un angle est un axe de symétrie de cet angle
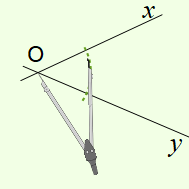
Pour tracer la bissectrice de l'angle, on trace un arc de cercle de centre O qui coupe chaque côté de l'angle en un point.
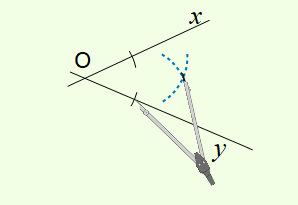
On trace deux arcs de cercle de même rayon ayant ces deux points pour centres. Ces arcs se coupent en un point.
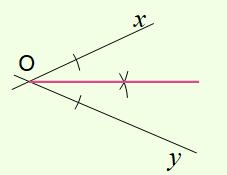
La bissectrice de l'angle est la demi-droite d'origine O passant par ce point.
Un triangle isocèle a un axe de symétrie qui est à la fois la médiatrice de sa base et la bissectrice de son angle principal.
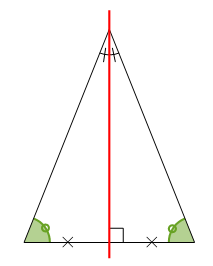
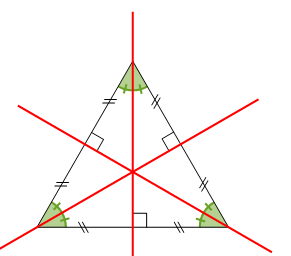
Un triangle équilatéral a trois axes de symétrie qui sont à la fois les médiatrices de ses côtés et les bissectrices de ses angles.
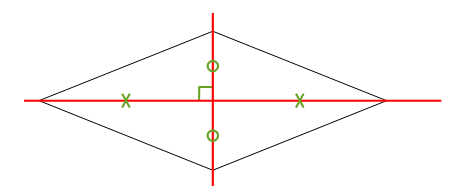
Un losange a deux axes de symétrie qui sont ses diagonales.
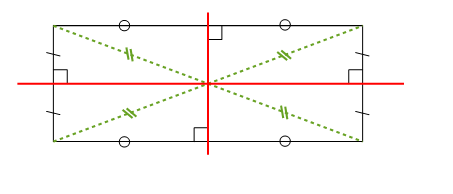
Un rectangle a deux axes de symétrie qui sont les médiatrices de ses côtés.
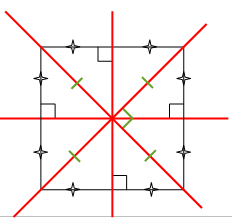
Un carré a quatre axes de symétrie qui sont les médiatrices de ses côtés et ses diagonales (un carré est à la fois un losange et un rectangle).
Dans un triangle isocèle, les angles à la base ont la même mesure.
Dans un triangle équilatéral, tous les angles ont la même mesure (60°).
Dans un losange, les diagonales se coupent en leur milieu et sont perpendiculaires.
Dans un rectangle, les diagonales se coupent en leur milieu et ont la même longueur.
Dans un carré, les diagonales se coupent en leur milieu, sont perpendiculaires et ont la même longueur.
En 6e, la bissectrice d'un angle est définie comme la demi-droite qui partage l'angle en deux angles adjacents de même mesure. La justification de la construction de la bissectrice à la règle et au compas est reliée à la symétrie axiale.
Connaître les propriétés relatives aux côtés, aux angles, aux diagonales pour le rectangle, le carré et le losange.
La symétrie axiale est mise en jeu pour mettre en évidence certaines propriétés.
Connaître et représenter des figures géométriques et des objets de l'espace. Utiliser leurs propriétés.
En situation, l’élève est capable de :
des outils (instruments de dessin, logiciels)
des définitions, des propriétés (en acte et sans nécessité d’indiquer ou de justifier la méthode choisie).
Partager: