Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Créer, c'est vivre deux fois.
| ^AOB | Angle nul | Angle aigu | Angle droit | Angle obtus | Angle plat |
|---|---|---|---|---|---|
| Figure : |  |
 |
 |
 |
 |
| Mesure : | 0° | Entre 0° et 90° | 90° | Entre 90° et 180° | 180° |
| Remarques : | A, O et B sont alignés | Plus petit qu'un "droit" | (OA) et (OB) sont perpendiculaires | Plus grand qu'un "droit" | A, O et B sont alignés Et O est entre A et B |
Tableau en vectoriel (zoomer sans déformation)
Tracer un triangle dans le cahier d'exercices tel que deux de ses angles soient obtus.
Et oui, c'est impossible. Pourquoi ?
La somme des angles d'un triangle est égale à 180°.
^ A + ^ B + ^ C = 180°
(Démonstration plus tard dans la progression, après avoir vu la symétrie centrale)
Il est donc évident que l'activité proposée avant était vouée à l'échec ! Un triangle avec deux angles obtus n'existe pas !
La somme de leurs mesures serait déjà supérieure à 180°!
A. Dans un triangle quelconque, si on connaît deux angles, on peut en déduire le troisième :
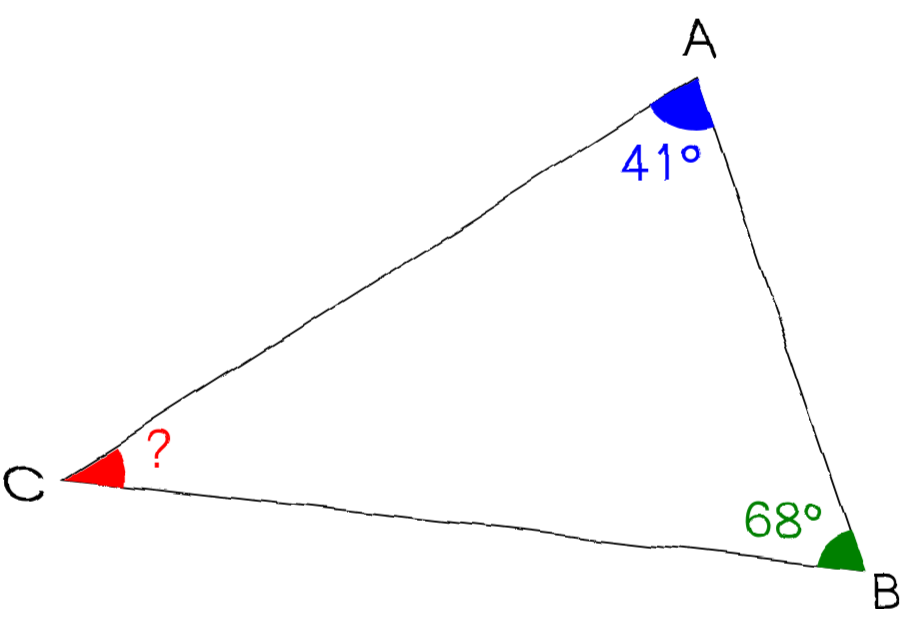
Dans le schéma ci-dessus (les mesures d'angles ne sont pas respectées) la somme des angles est 180°
^ A + ^ B + ^ C = 180°
41° + 68° + ^ C = 180°
109° + ^ C = 180°
^ C = 180° - 109° = 71°
ABC est un triangle rectangle en A tel que ^ABC = 54°. Après avoir fait un schéma, calculer ^BCA.
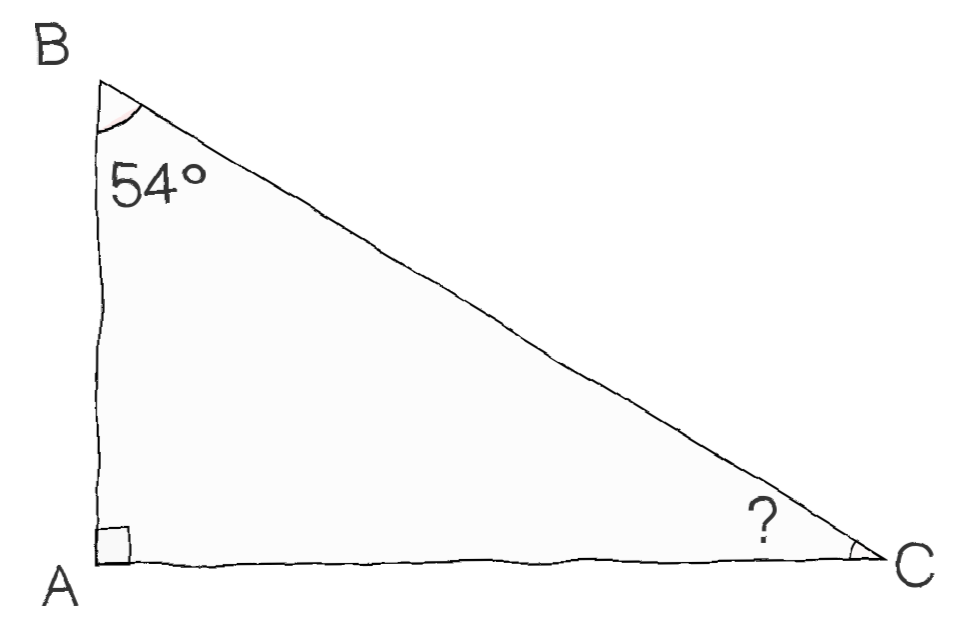
Dans le schéma ci-dessus (les mesures d'angles ne sont pas respectées) la somme des angles est 180°
^ A + ^ B + ^ C = 180°
90° + 54° + ^ C = 180°
144° + ^ C = 180°
^ C = 180° - 144° = 36°
On appelle angles complémentaires deux angles dont la somme est 90°.
Dans un triangle rectangle les angles aigus sont complémentaires.
^ B + ^ C = 90°
54° + ^ C = 90°
^ C = 90° - 54° = 36°
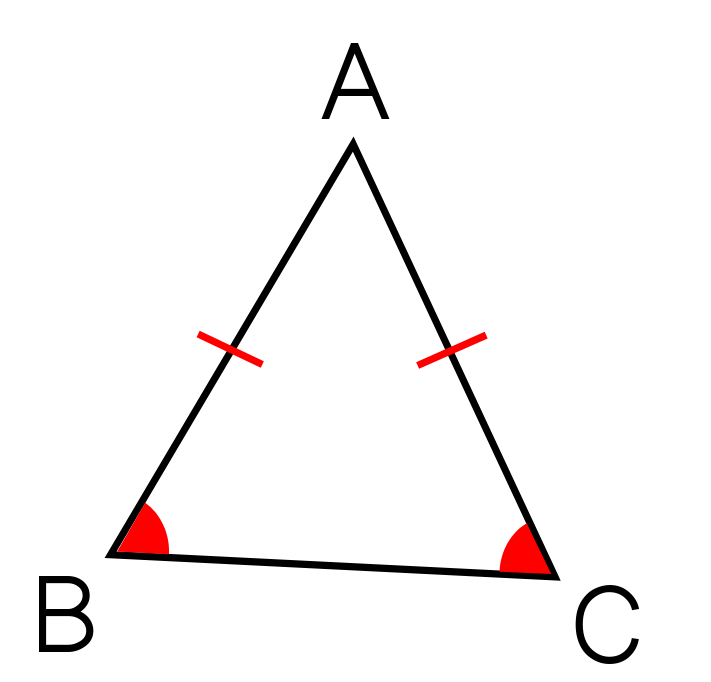
On appelle triangle isocèle un triangle qui a deux côtés égaux. Le point A est l'intersection de ces deux côtés égaux : c'est le sommet principal.. Les angles des deux autres sommets sont appelés angles de base.
Dans un triangle isocèle les angles de base sont égaux.
^ABC = ^ACB
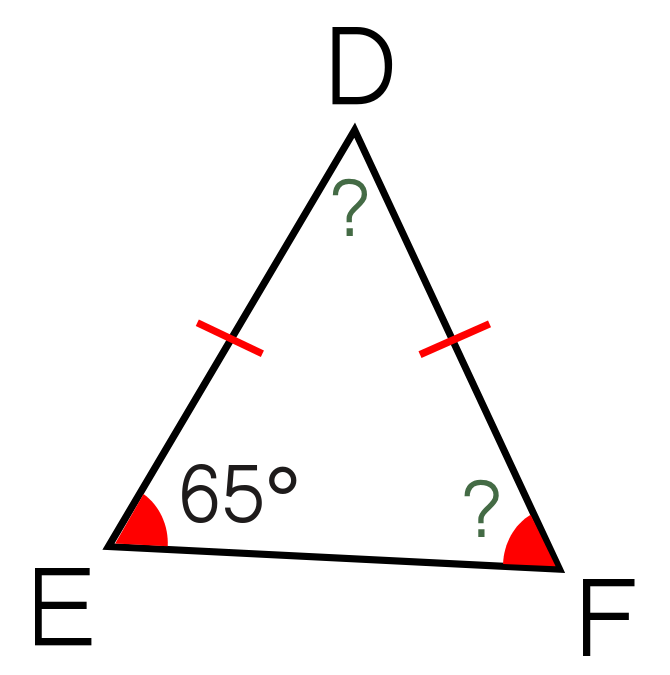
Dans le triangle DEF isocèle en D, les angles de base sont égaux :
^DEF = ^DFE = 65°
La somme des angles est 180°
^DEF + ^DFE + ^EDF = 180°
65° + 65° + ^EDF = 180°
130° + ^EDF = 180°
^EDF = 180° - 130° = 50°
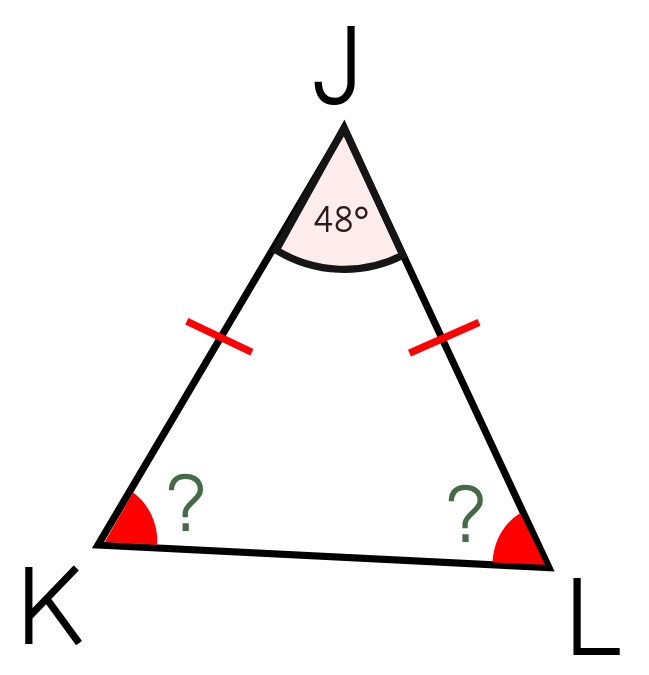
Dans le triangle JKL isocèle en J la somme des angle est 180°:
^KJL + ^JLK + ^LKJ = 180°
Et les angles de bases sont égaux :
^JLK = ^LKJ
D'où :
^KJL + 2 ×^JLK = 180°
48° + 2 ×^JLK = 180°
2 ×^JLK = 180° - 48°
2 ×^JLK = 132°
^JLK = 132 2 = 66°
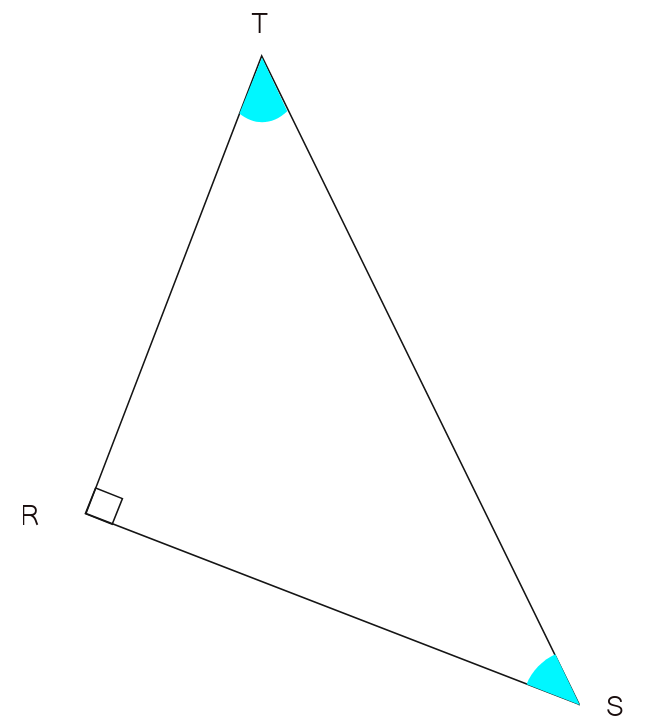
Dans le triangle RTS rectangle et isocèle en R, les angles de base sont égaux et complémentaires :
^RTS = ^RST
^RTS + ^RST = 90°
^RTS = ^RST = 90 2 = 45°
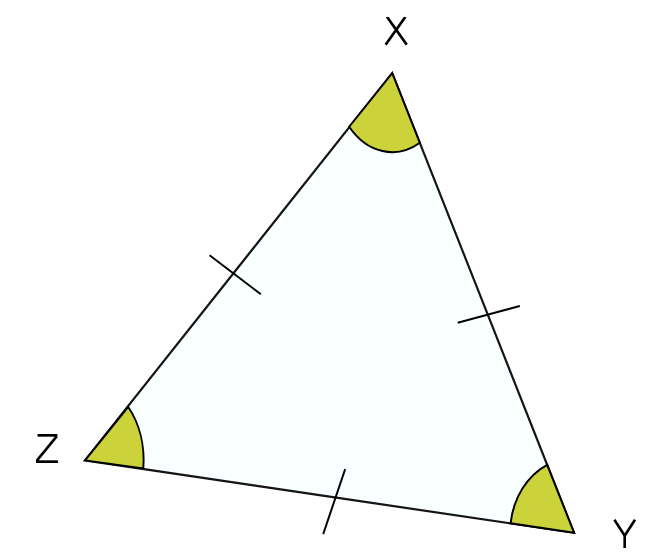
Les trois angles du triangle équilatéral XYZ sont égaux et leur somme est 180° , d'où :
^ZXY = ^XYZ = ^YZX = 180 3 = 60°
L’élève connaît et utilise :
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: