
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Si les anglicismes vous soulèvent le coeur, optez pour un pacemaker.
D'après vocabulax.com



Deux triangles sont égaux s’ils sont superposables.
Cela veut dire qu’on peut poser l’un sur l’autre en le déplaçant, en le tournant ou même en le retournant pour qu’ils coïncident parfaitement.
On dit que deux triangles sont semblables quand leurs trois angles sont égaux deux à deux.
Les triangles suivants sont semblables :
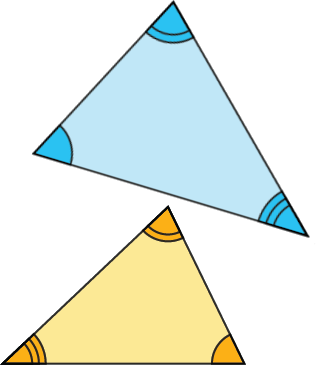
Deux triangles égaux sont semblables. Mais deux triangles semblables ne sont pas forcément égaux.
🐾 Un chien est un mammifère, mais un mammifère n'est pas forcément un chien !
Si deux triangles sont égaux alors ils sont semblables.
Pour des triangles égaux la définition signifie que leurs trois côtés et leurs trois angles sont égaux.
Deux triangles sont égaux quand ils ont un côté de même longueur et deux angles de même mesure.
Vous pouvez même démontrer, depuis la cinquième, que deux triangles qui ont deux angles égaux ont trois angles égaux ! 🤔
Si deux triangles ont deux angles égaux alors ils sont semblables.
Deux triangles sont égaux quand ils ont deux côtés de même longueur et l’angle formé par ces côtés de même mesure.
Les trois propriétés suivantes sont d'une importance capitale pour la suite de l'année !
Si deux triangles sont semblables alors l’un est l’agrandissement de l’autre.
Si deux triangles sont semblables alors l’un est la réduction de l’autre.
Si deux triangles sont semblables alors leurs côtés sont proportionnels.
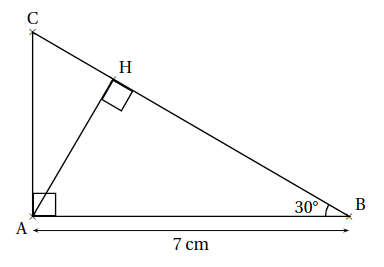
À la question 1., on a reproduit la figure en vraie grandeur.
À la question 2, on a prouvé que AH= 3, 5 cm.
3. Démontrer que les triangles ABC et HAC sont semblables.
4. Déterminer le coefficient de réduction permettant de passer du triangle ABC au triangle HAC.


Un quadrilatère est un polygone ayant quatre côtés.
Un trapèze est un quadrilatère ayant deux côtés parallèles.
Un trapèze rectangle est un trapèze ayant un angle droit (et donc deux !).
Un parallélogramme est un quadrilatère ayant des côtés opposés parallèles.
Un rectangle est un quadrilatère ayant quatre angles droits. (3 suffisent!)
Un losange est un quadrilatère dont les quatre côtés sont égaux.
Un carré est un quadrilatère rectangle et losange.
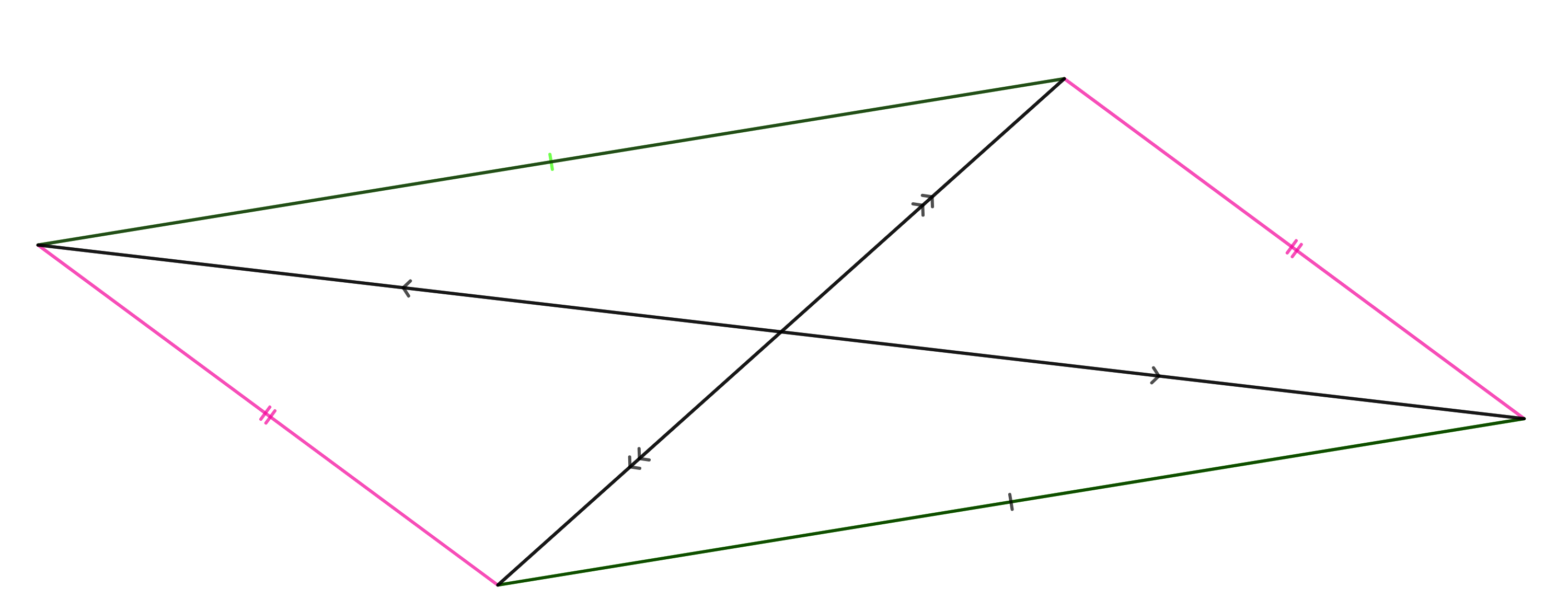
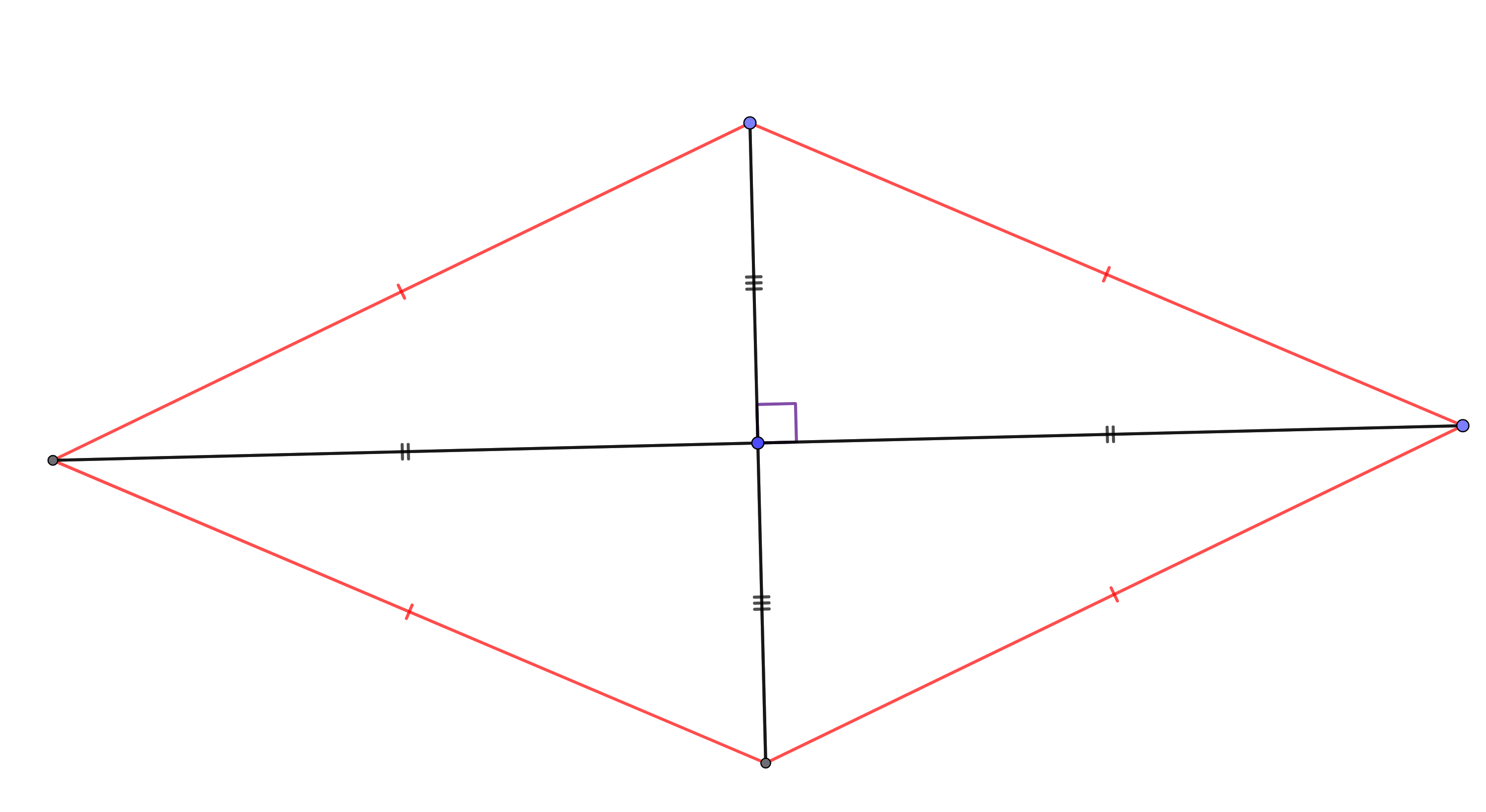
Si un quadrilatère est un parallélogramme alors :
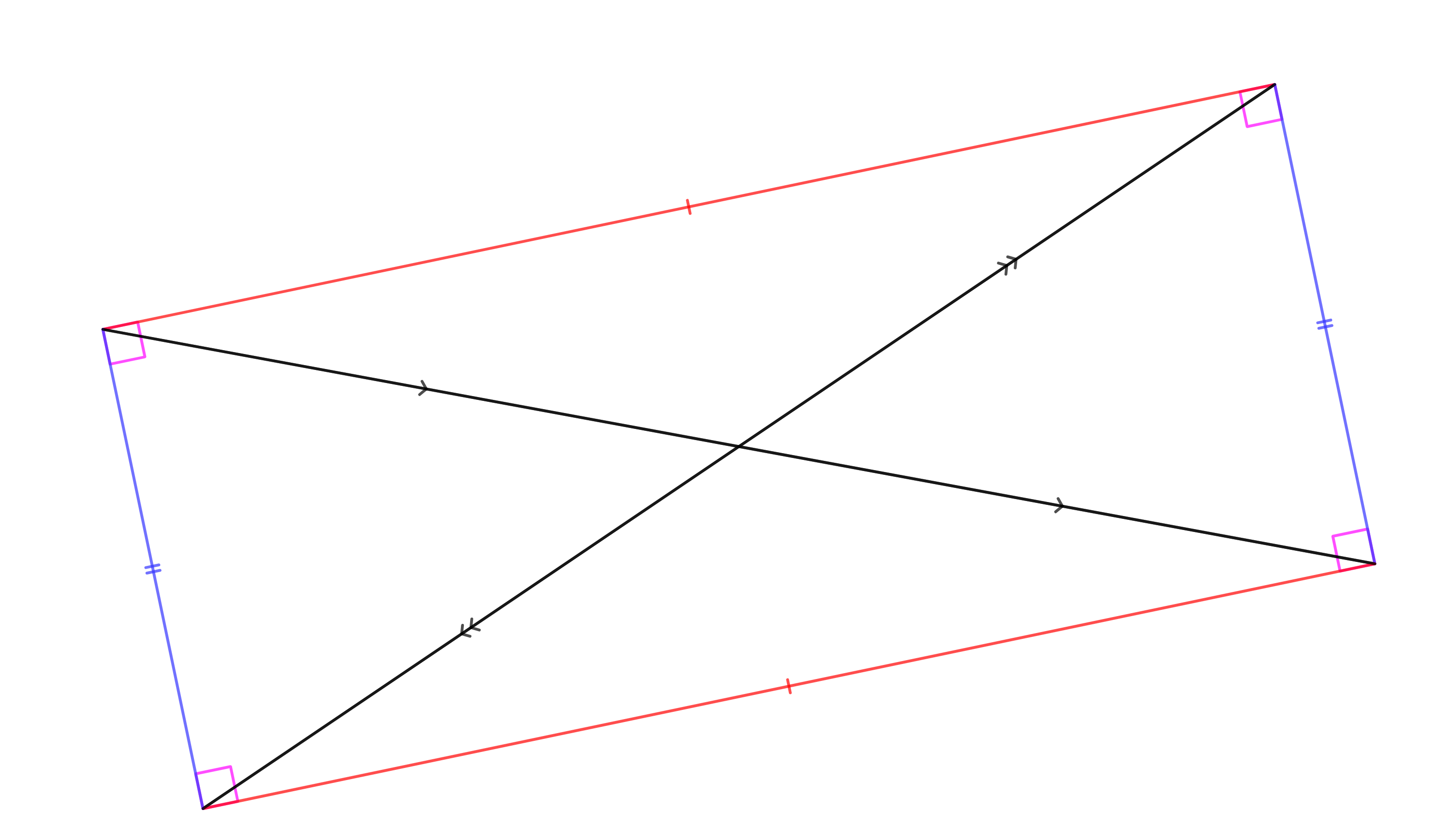
Si un quadrilatère est un losange alors :
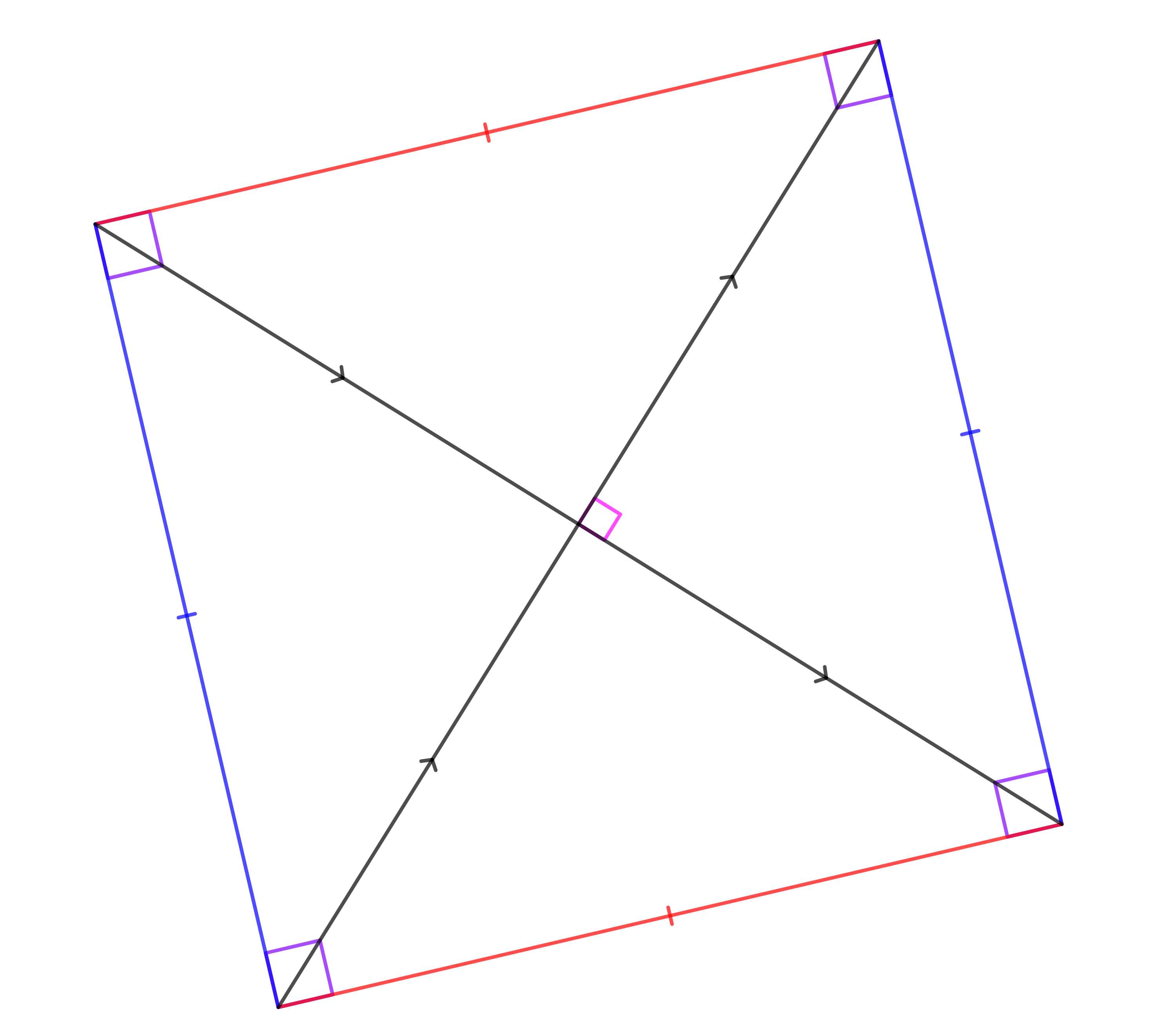
Si un quadrilatère est un rectangle alors :
Si un quadrilatère est un carré alors :
Lorsqu’on identifie une figure géométrique, il est important de justifier cette reconnaissance en précisant les propriétés utilisées : parallélisme ou égalité des côtés, nature des angles, caractéristiques des diagonales, etc.
Si les diagonales d’un quadrilatère se coupent en leur milieu alors c’est un parallélogramme.
Si les côtés opposés d’un quadrilatère sont parallèles alors c’est un parallélogramme.
Si les côtés opposés d’un quadrilatère sont égaux alors c’est un parallélogramme.
Si les diagonales d’un parallélogramme sont de même longueur alors c’est un rectangle.
Si un parallélogramme a un angle droit alors c’est un rectangle.
Si les diagonales d’un parallélogramme sont perpendiculaires alors c’est un losange.
Si deux côtés consécutifs d’un parallélogramme sont égaux alors c’est un losange.
Si un parallélogramme est rectangle et losange alors c’est un carré.

On donne:


Au cycle 4, l’élève continue de s’appuyer sur une géométrie perçue par les sens et contrôlée par les instruments (règle, compas, équerre), mais évolue progressivement vers une approche plus rigoureuse, dans laquelle les propriétés sont validées par des raisonnements et des démonstrations. La manipulation, la construction, l’observation et la conjecture conservent leur place, mais sont désormais reliées à une argumentation structurée.
L’élève approfondit sa connaissance des figures planes (triangles, quadrilatères, cercles, polygones réguliers), et mobilise leurs propriétés géométriques et métriques dans des contextes variés. Les configurations remarquables sont introduites à partir de situations concrètes qui justifient leur étude. Les théorèmes de Pythagore (en 4e) et de Thalès (en 3e), ainsi que les rapports trigonométriques dans le triangle rectangle, sont abordés de manière progressive.
L’utilisation d’outils numériques (logiciels de géométrie dynamique, programmation, tableurs) permet d’explorer des figures, de formuler des conjectures, et d’automatiser certaines constructions. Les frises, rosaces et pavages offrent un cadre riche pour explorer les transformations géométriques (symétries, rotations, translations, agrandissements).
Pour un approfondissement, consulter les ressources officielles : Programme de mathématiques du cycle 4 (BOEN 2015) et Ressources Eduscol pour le cycle 4.

Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager :