Pas de violence, c'est les vacances...
Saturnin (Brice de Nice) (sur mon T shirt!)
Un polygone est une figure géométrique fermée, formée de plusieurs segments.
Les segments sont les côtés du polygone.
Les points d'intersection des segments sont les sommets du polygone.
Pour nommer un polygone, on commence par un sommet, et on les nomme tous, en suivant les côtés de ce polygone (Dans le sens qu'on veut !)
Un polygone croisé est un polygone dont certains côtés se coupent.
Dans le cas contraire, on parle de polygones simples.
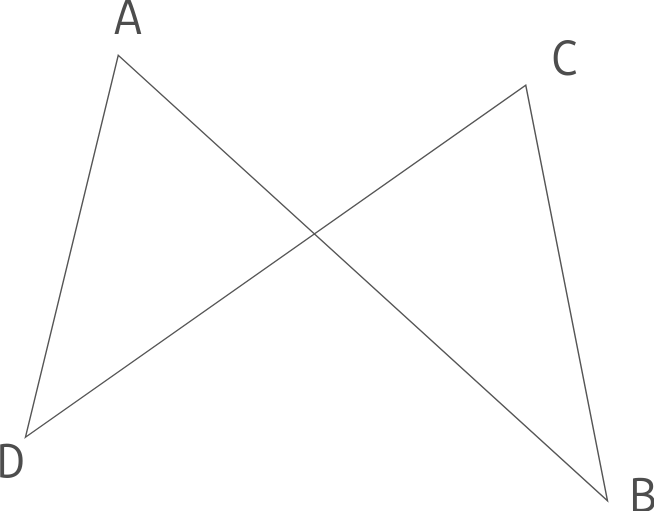
Le polygone suivant est un quadrilatère (polygone à 4 côtés) croisé. Son nom (par exemple) est ABCD.
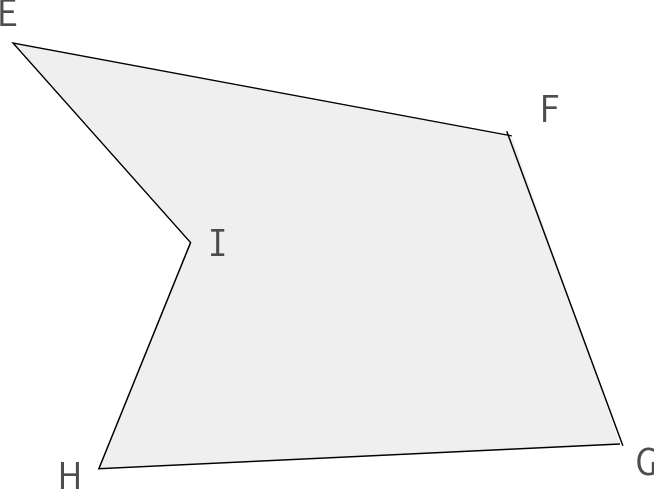
Le polygone suivant est un pentagone (polygone à 5 côtés) simple (non croisé). Son nom (par exemple) est EFGHI.
| Nombre de sommets | Nom du polygone |
|---|---|
| 3 | Triangle |
| 4 | Quadrilatère |
| 5 | Pentagone |
| 6 | Hexagone |
| 7 | Heptagone |
| 8 | Octogone |
| 9 | Ennéagone |
| 10 | Décagone |
| 11 | Hendécagone |
| 12 | Dodécagone |
| 13 | Tridécagone |
| 14 | Tétradécagone |
| 15 | Pentadécagone |
| 16 | Hexadécagone |
On appelle triangle rectangle un triangle qui a un angle droit.
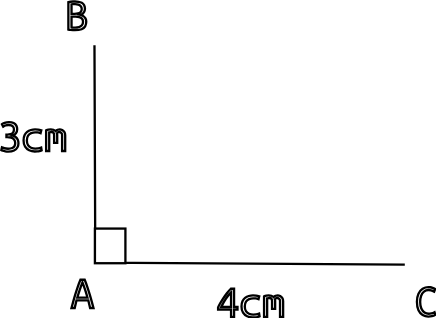
Construire le triangle ABC rectangle en A tel que AB=3cm et AC=4cm.
ici, on connaît les deux côtés de l'angle droit. On commence par tracer ces deux côtés perpendiculaires:
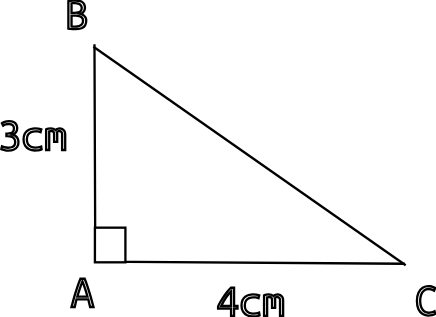
Et on termine par tracer le segment [BC]
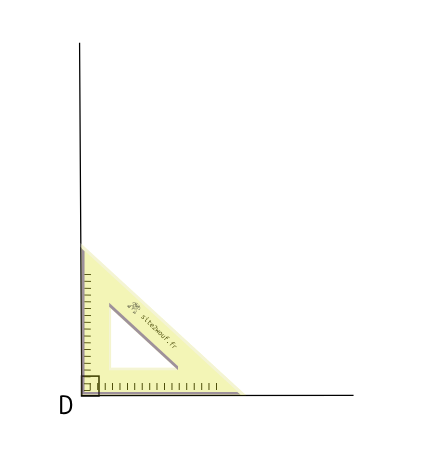
Construire le triangle DEF rectangle en D tel que DE=3cm et EF=5cm.
ici, on ne connaît pas les deux côtés de l'angle droit. On commence par tracer deux demi-droites perpendiculaires en D:
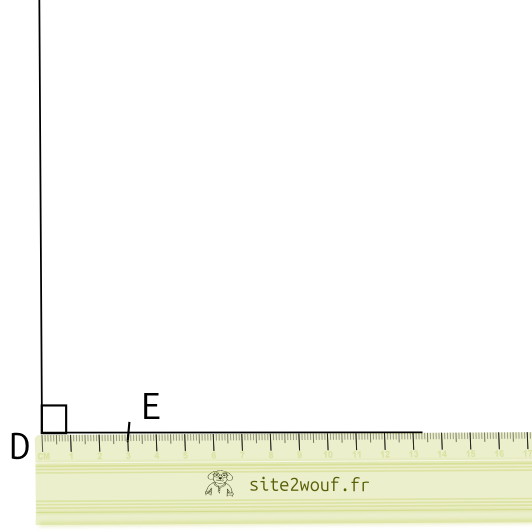
On place le point E:
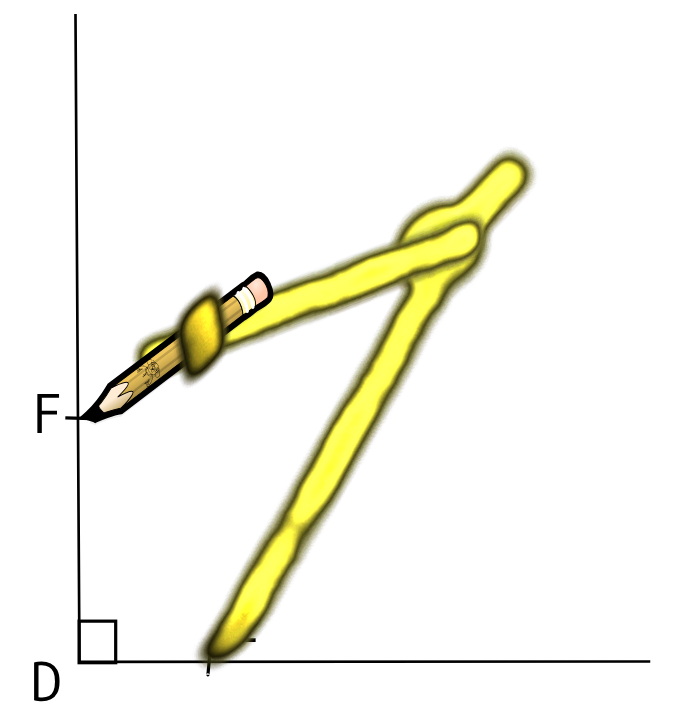
On ouvre le compas de 5cm, c'est à dire de la longueur du segment [EF]
![On ouvre le compas de 5cm, c'est à dire de la longueur du segment [EF]](coll/l6/triangles_quadrilateres/ouverture_compas.png)
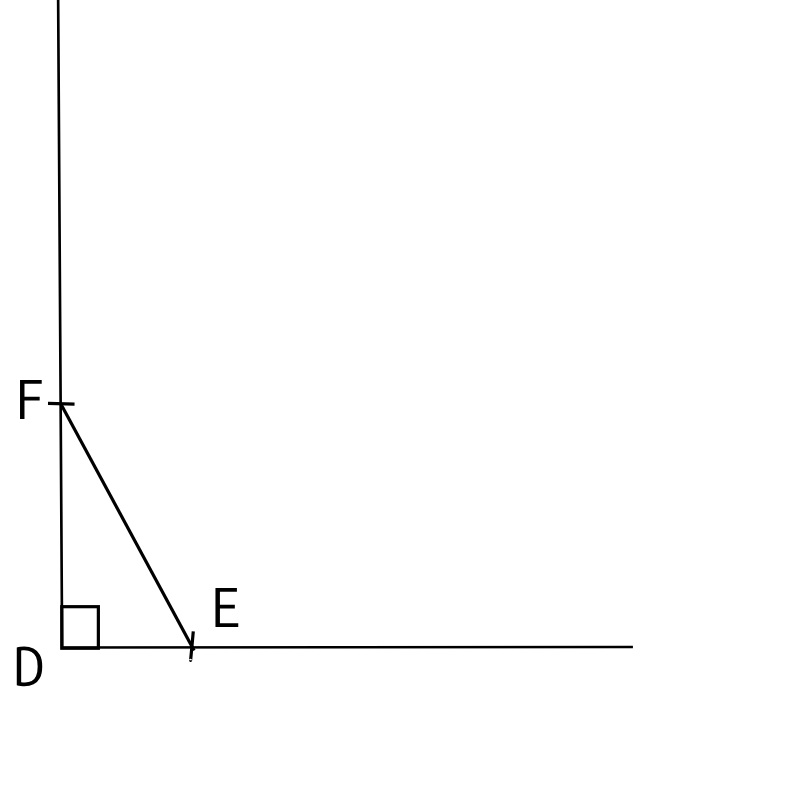
F est l'intersection de l'arc de cercle de centre E et de rayon 5 cm avec l'autre demi-droite.
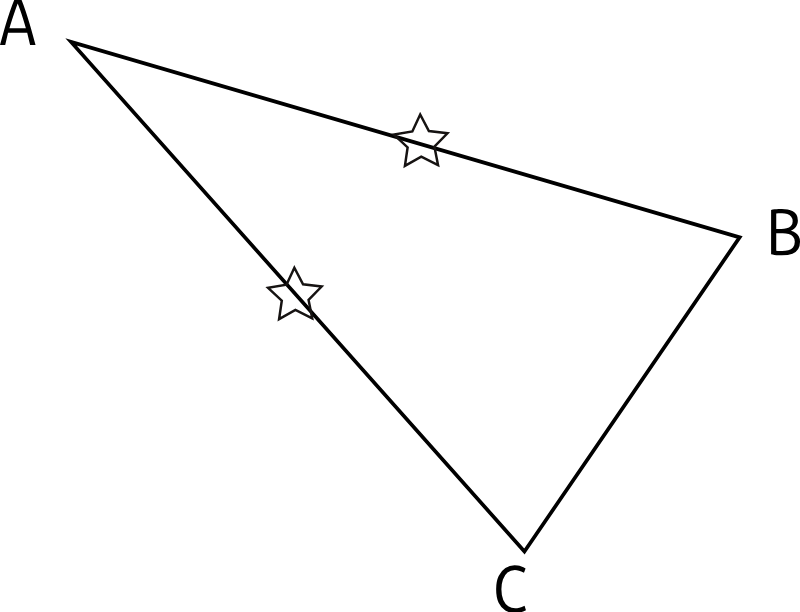
On appelle triangle isocèle un triangle qui a deux côtés égaux.
Dans le triangle ABC, le point A est l'intersection des côtés égaux, on l'appelle le le sommet principal
Le côté [BC] est opposé au sommet principal A.Il est appelé base du triangle isocèle.
La médiatrice de la base est un axe de symétrie du triangle isocèle: Elle est perpendiculaire à la base, en son milieu et passe par le sommet principal (qui est équidistant des extrémités de la base.) On peut en déduire que les angles de base dont égaux:
^ABC = ^ACB
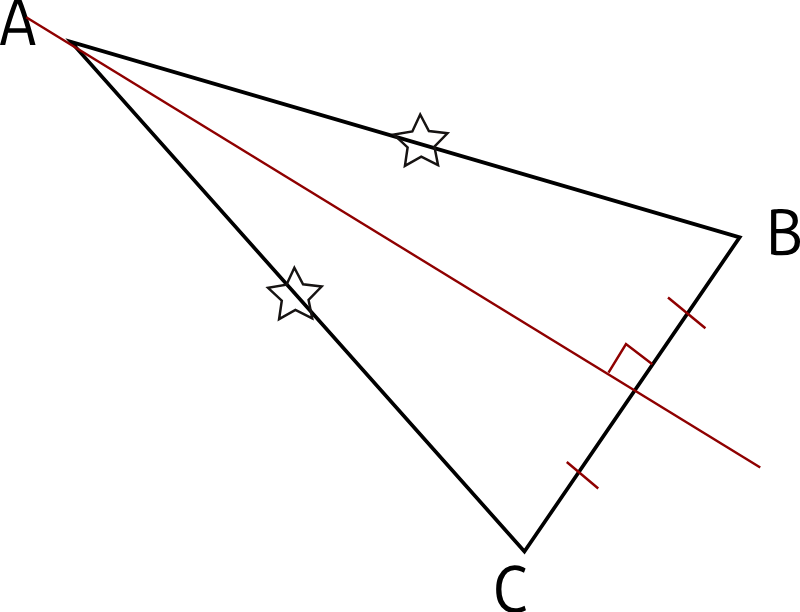
Après avoir tracé la base, on trouve le sommet principal à l'intersection de deux arcs de cercle de même rayon et de centres respectifs les extrémités de la base.
On pense à coder les deux côtés égaux !
Exemples en exercice
On appelle triangle équilatéral un triangle qui a ses 3 côtés égaux.
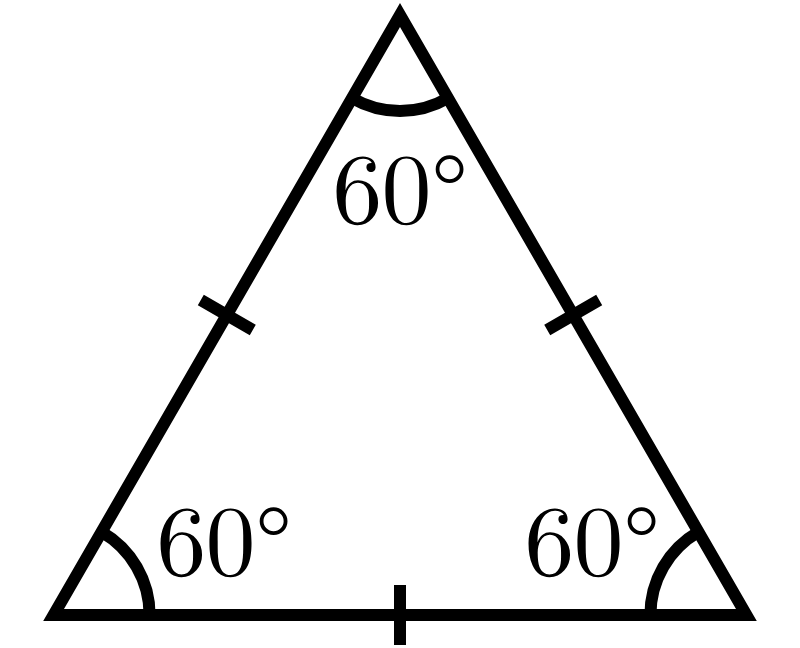
Les médiatrices des côtés sont des axes de symétrie, elles sont médiatrices des côtés.
Les 3 angles sont égaux (60°)
Après avoir tracé un côté, on trouve le sommet opposé à l'intersection de deux arcs de cercle de même rayon et de centres respectifs les extrémités du segment.
On pense à coder les côtés égaux !
Exemples en exercices
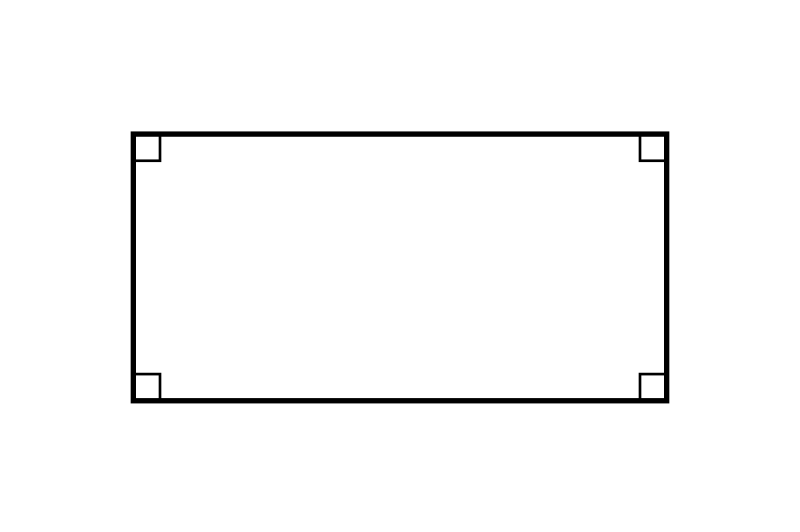
On appelle rectangle un quadrilatère qui a quatre angles droits.
Les cotés opposés d'un rectangle sont parallèles et de la même longueur.
Les diagonales d'un rectangle sont de la même longueur et ont le même milieu.
Aucune difficulté quand on connaît deux côtés consécutifs et qu'on dispose de son équerre !
Si on ne les connaît pas tous les deux (mais la diagonale) il faut disposer d'un compas: Exemples en exercice
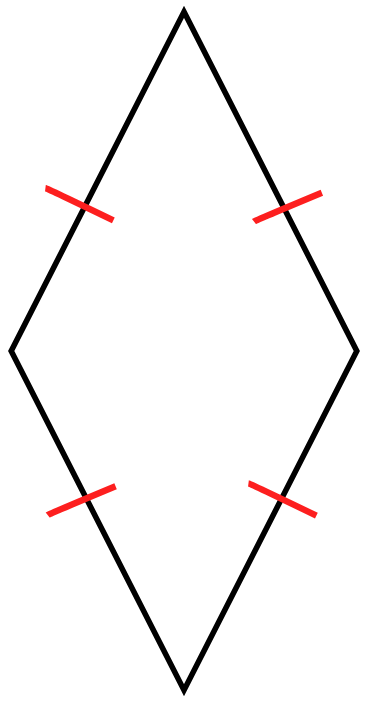
On appelle losange un quadrilatère qui a ses quatre côtés égaux.
Les diagonales d'un losange sont ses axes de symétrie, elles sont perpendiculaires et ont même milieu.
Les côtés opposés d'un losanges sont parallèles et égaux.
Les angles opposés d'un losanges sont égaux.
Exemples en exercices
On appelle carré un rectangle losange.
Un carré a donc toutes les propriétés du rectangle et du losange.
En exercices
Partager: