Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
La vie se passe à désirer ce qu'on n'a pas, à regretter ce qu'on n'a plus.
Dans le triangle rectangle ABC, ^BAC est l'angle droit, le côté opposé à ^BAC (en face de ^BAC) est [BC], c'est l'hypoténuse.
[AC] est le côté opposé à l'angle ^ABC
[AB] est le côté adjacent à l'angle ^ABC
[AB] est le côté opposé à l'angle ^ACB
[AC] est le côté adjacent à l'angle ^ACB
Dans le triangle ABC, rectangle en A, le cosinus, les expressions du cosinus, du sinus et de la tangente d’un angle aigu sont données par
cos ^ABC= côté adjacent à ^ABC hypoténuse = AB BC
sin ^ABC= côté opposé à ^ABC hypoténuse = AC BC
tan ^ABC= côté opposé à ^ABC côté adjacent à ^ABC = AC AB
De même :
cos ^ACB= côté adjacent à ^ACB hypoténuse = ... ...
sin ^ACB= côté opposé à ... hypoténuse = ... ...
tan ^ACB= .................... .................... = ... ...
cos ^ACB= côté adjacent à ^ACB hypoténuse = AC BC
sin ^ACB= côté opposé à ^ACB hypoténuse = AB BC
tan ^ACB= côté opposé à ^ACB côté adjacent à ^ACB = AB AC
SOH CAH TOA n'est pas une formule magique, mais un moyen mnémotechnique pour retenir les formules ci-dessus:
ABC est un triangle rectangle en A. On donne AB = 5 cm et ^ABC = 35°
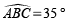
Dans le triangle ABC, rectangle en A
tan ^ABC = AC AB = AC 5
D’où
AC = 5 ×tan ^ABC = 5 × tan(35°)≈ 3,5 cm
Dans le triangle FCO rectangle en F,
on sait que :
Après avoir fait un schéma, calcule l’arrondi au degré près de la mesure de l’angle ^COF.
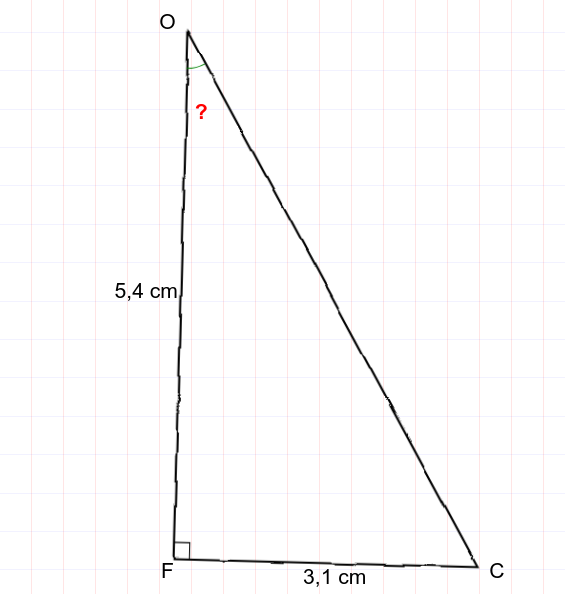Dans le triangle FCO, rectangle en F, on cherche une relation entre l’angle ^COF, son côté opposé et son côté adjacent.tan(^COF) = FCFO
tan(^COF) = 3,15,4
^COF = arctan(3,15,4) ≈ 30°
arctan de la calculatrice pour déterminer un angle à partir d’un rapport de longueurs.
Page d'un livre de 1619 contenant une table trigonométrique
Par Matthias Bernegger , Domaine public.
Avant l’existence des calculatrices de poche, les tables trigonométriques étaient essentielles. Aujourd’hui, c’est la calculatrice qui a ce rôle… à condition de bien savoir s’en servir.
Les touches arcos, arcsin et arctan permettent de trouver un angle à partir d’un rapport trigonométrique.
Ces touches sont les fonctions inverses des touches cos, sin et tan.
Par exemple, si on connait la valeur du cosinus d’un angle (comme 0,5), on peut utiliser arcos(0,5) pour retrouver cet angle :
^ABC mesure (exactement) 60°.
Sur une calculatrice scolaire comme la Casio fx 92, ces fonctions sont accessibles via la touche 2nde, puis en appuyant sur cos, sin ou tan.
On voit alors apparaître cos⁻¹, sin⁻¹ ou tan⁻¹, qui correspondent respectivement à arcos, arcsin et arctan.
Assurez-vous que votre calculatrice est bien réglée en degrés pour obtenir des résultats conformes à ce qui est attendu au collège.
Pour s'assurer que votre calculatrice affiche les angles en **degrés**, la méthode peut varier légèrement selon les modèles, mais voici la démarche générale pour la Casio fx-92 (et la plupart des calculatrices scientifiques) :
Une fois cette manipulation effectuée, un petit "D" ou "DEG" devrait apparaître en haut de l'écran de votre calculatrice, confirmant qu'elle est bien réglée en degrés.
Vérifiez-le en tapant cos(60°) : le résultat doit être 0.5.
OFFICIEL
Triangle rectangle : relations trigonométriques
Connaître et utiliser dans le triangle rectangle des relations entre le cosinus, le sinus ou la tangente d’un angle aigu et les longueurs de deux côtés du triangle.
Utiliser la calculatrice pour déterminer des valeurs approchées :
La définition du cosinus a été vue en 4e. Le sinus et la tangente d’un angle aigu seront introduits comme rapports de longueurs dans un triangle rectangle, ou à l’aide du quart de cercle trigonométrique.
On n’utilisera pas d’autre unité que le degré décimal.
Le recours au logiciel ou à la calculatrice est attendu, notamment pour l’accès à une valeur d’un angle connaissant un rapport trigonométrique.
Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager: