
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
La mort semble bien moins terrible, quand on est fatigué.
Simone de Beauvoir



| km | hm | dam | m | dm | cm | mm |
| 1 | 5 | 2 |
Le nombre écrit dans le tableau peut se lire dans toutes les unités de la ligne 1, en se rappelant que l'unité donne l'emplacement de la virgule et que les cases vides contiennent des zéros (parfois inutiles dans l'écriture décimale.)
0,0152 km = 0,152 hm = 1,52 dam = 15,2 m =152 dm = 1 520 cm = 15 200 mm
| km² | hm² | dam² | m² | dm² | cm² | mm² | |||||||
| ha | a | ||||||||||||
| 5 | 0 | 3 | 5 | 5 | |||||||||
La deuxième ligne est constituée d'unités agraires (l' hectare et l'are qui servent pour évaluer l'aire de terrains).
A l'aide du tableau vous pouvez voir qu'un champ de 50 355 m² a une aire d'environ 5 ha en effet :
50 355 m² = 5,0355 ha
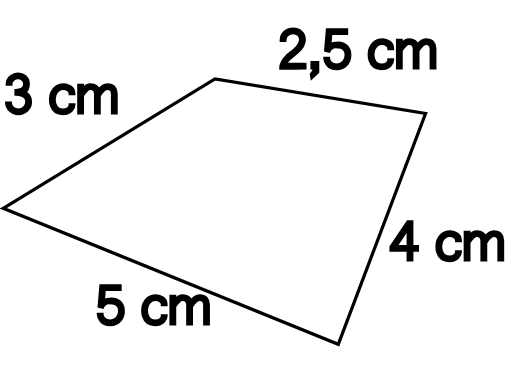
Le périmètre d’une figure est la longueur de son contour.
On imagine une fourmis qui fait le tour du polygone en calculant sa distance parcourue:
Ici on a :
P = 5 + 4 + 2,5 + 3 = 14,5 cm
On ne dispose pas de formule pour calculer l'aire d'un polygone quelconque !
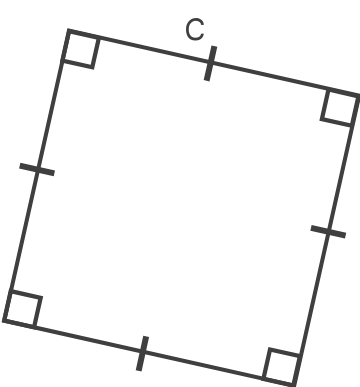
Le périmètre d'un carré de côté c est donné par la formule suivante :
P = 4 ×c
L'aire d'un carré de côté c est donnée par la formule suivante :
A = c × c = c²
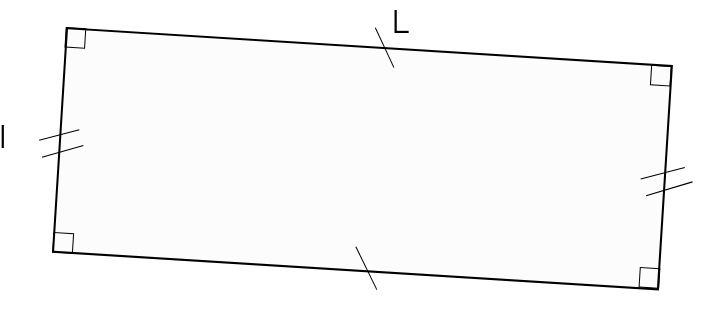
Le périmètre d'un rectangle de longueur L et de largeur l est donné par la formule suivante :
P = 2 × (L + l) = 2 × L + 2 × l
L'aire d'un rectangle de longueur L et de largeur l est donnée par la formule suivante :
A = L × l
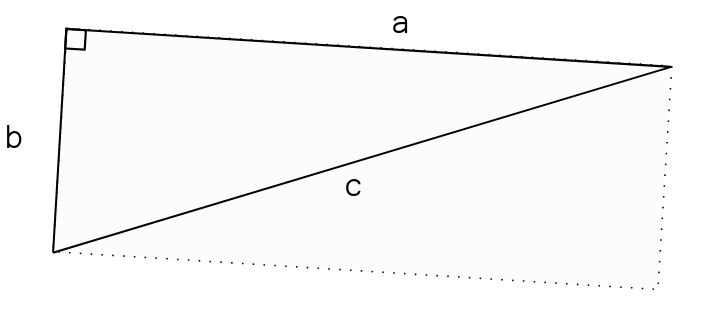
Le périmètre se calcule comme pour tous les polygones quelconques en ajoutant les mesures des segments qui le composent:
Ici on a:
P = a + b + c
L'aire d'un triangle rectangle dont les côtés de l'angle droit ont pour mesures a et b est donnée par la formule suivante :
A = a × b 2
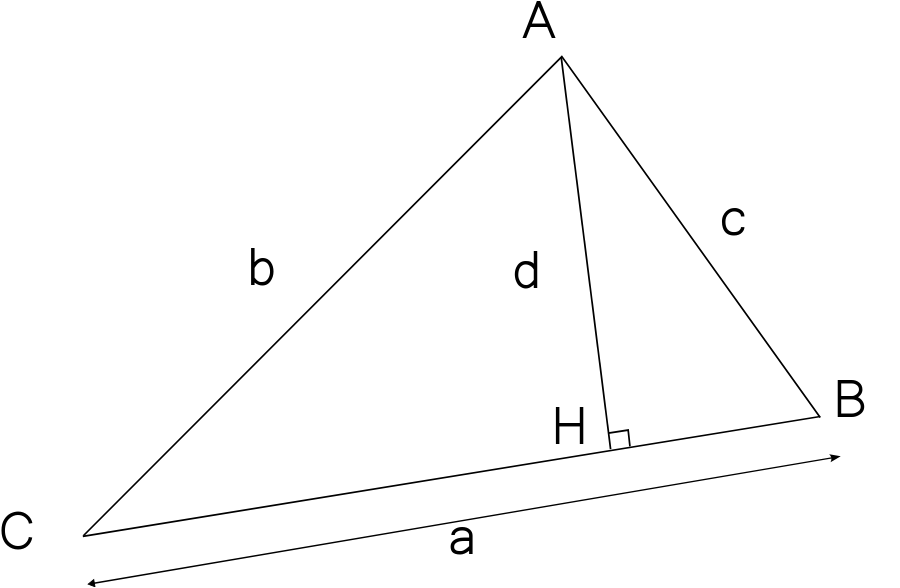
Dans le triangle quelconque ci-dessus (AH) ⊥ (BC) . On dit que [AH] est la hauteur issue de A ou que [AH] est la hauteur relative au coté [BC]. Le point H est appelé pied de la hauteur.
Le périmètre se calcule comme pour tous les polygones quelconques en ajoutant les mesures des segments qui le composent:
Ici on a:
P = a + b + c
L'aire d'un triangle est égale à la moitié du produit de la longueur d'un côté pas sa hauteur relative.
Ici on a :
A = a × d 2
Quand il y a un angle obtus dans le triangle, le pied de la hauteur peut se situer hors du segment :
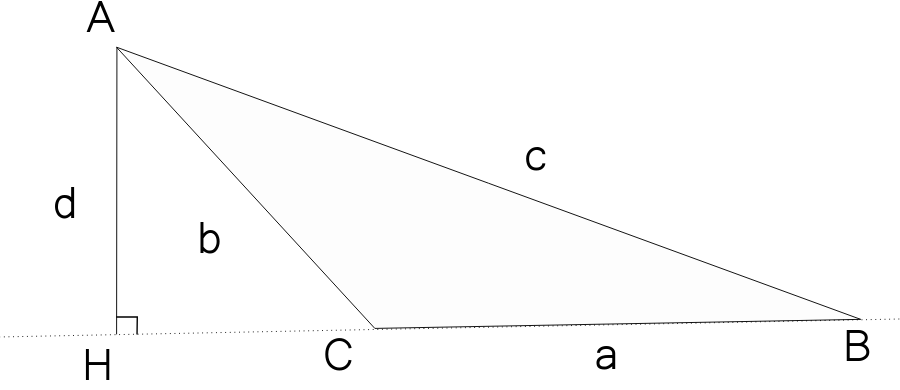
Mais cela ne change rien, on a encore:
P = a + b + c
et
A = a × d 2
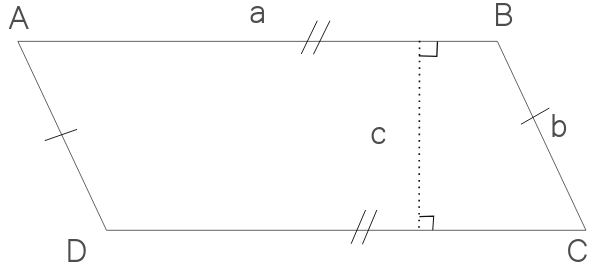
Le périmètre pourrait se calculer comme pour tous les polygones quelconques en ajoutant les mesures des segments qui le composent, mais ses côtés opposés étant égaux on a:
P = 2 × (a + b) = 2 × a + 2 × b
L'aire d'un parallélogramme est égale au produit de la longueur d'un côté par la hauteur relative à ce côté. Ici on a :
A = a × c

Le cercle de centre O et de rayon r cm est constitué de tous les points à exactement r cm de O.
Le disque de centre O et de rayon r cm est constitué de tous les points dont la distance à O est inférieure (ou égale) à r cm.
Même si ces deux objets se ressemblent, ils sont très différents. On parlera du périmètre d'un cercle et de l'aire d'un disque.
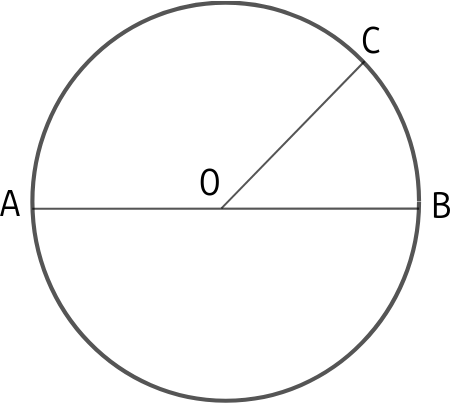
Le périmètre de ce cercle de centre O, de rayon r et de diamètre d est donné par la formule :
P = 2 × π × r = π × d
L'aire de ce disque, de rayon r et de diamètre d est donné par la formule :
A = π × r × r = π × r 2
| Figure | Périmètre | Aire |
|---|---|---|
| Polygone quelconque | P = somme des côtés | pas de formule |
| Carré (c : côté) | P = 4 × c | A = c × c |
| Rectangle (L : longueur, l : largeur) | P = 2 × (L + l) | A = L × l |
| Triangle rectangle (a, b : côtés de l’angle droit) | P = a + b + c |
A = a × b 2 |
| Triangle quelconque (a : base, d : hauteur relative) | P = a + b + c |
A = a × d 2 |
| Parallélogramme (a et b : cotés consécutifs , h : hauteur relative à a) | P = ( a + b ) × 2 |
A = a × h 2 |
| Cercle et disque (r : rayon, d : diamètre) | P = 2 × π × r = π × d | A = π × r2 |
Toujours indiquer les unités dans tes résultats : m, cm, m², cm²…
Dans le domaine « Grandeurs et mesures », les élèves approfondissent leur compréhension des longueurs, périmètres, aires et volumes. Ils développent leur capacité à modéliser et résoudre des problèmes en mobilisant les relations entre grandeurs, en manipulant les unités et en utilisant des formules adaptées aux figures planes et aux solides usuels.
Les attendus de fin de cycle incluent la capacité à :
L'objectif est d'amener les élèves à utiliser des outils de mesure, des instruments de tracé et des raisonnements mathématiques pour analyser des situations de la vie courante ou des problèmes mathématiques, conformément aux programmes officiels du cycle 4.

Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager :