L'eau, c'est la vie. Elle constitue, de loin, notre bien le plus précieux.
Une fraction décimale est une fraction dont le dénominateur est égal à 10, 100, 1 000, etc (le chiffre 1 suivi de un ou plusieurs zéros)
Les fractions suivantes sont des fractions décimales :
$$ \dfrac{3}{1~000} $$ $$ \dfrac{48}{10~000} $$ $$ \dfrac{145}{10} $$Dans ce nombre décimal 3 est le chiffre des millièmes et aussi le nombre de millièmes.
$$ \dfrac{48}{10~000} = 0,0048 $$Ici 8 est le chiffre des dix-millièmes et 48 le nombre de dix-millièmes.
$$ \dfrac{145}{10} = 14,5 $$Et là, 5 est le chiffre des dixièmes et 145 le nombre de dixièmes.
Les Arabes ont joué un rôle crucial dans le développement des Mathématiques, notamment en matière de calcul. Vers le 10ème siècle, le mathématicien (et astronome) arabe Ibrahim ibn Sina, plus connu sous le nom d'Avicenne, a posé les bases de l'utilisation des fractions décimales. Il a compris l'intérêt de représenter des quantités plus petites que l'unité en utilisant des dixièmes, des centièmes, et ainsi de suite. Cette idée était révolutionnaire car elle s'appuyait sur notre système de numération décimal, basé sur le nombre 10.
Cependant, il a fallu attendre plusieurs siècles pour que la notation des nombres décimaux se standardise. La virgule, que nous utilisons aujourd'hui pour séparer la partie entière d'un nombre de sa partie décimale, n'a pas été adoptée immédiatement.
Différentes notations ont cohabité pendant un certain temps. Certains mathématiciens utilisaient un point, d'autres un petit cercle ou encore une barre verticale. C'est finalement la virgule qui s'est imposée, grâce notamment aux travaux de mathématiciens comme John Napier au 17ème siècle.
La division décimale est l'opération qui permet de calculer le quotient décimal (ou une valeur approchée de ce quotient) de deux nombres décimaux.
L'algorithme de division non abrégée, encore appelé division longue, sert à déterminer une écriture décimale du quotient de deux nombres entiers. C'est une extension de la division euclidienne. D'un point de vue pratique, il consiste à continuer la procédure, en « descendant des zéros », les nouveaux chiffres calculés s'ajoutant après la virgule.
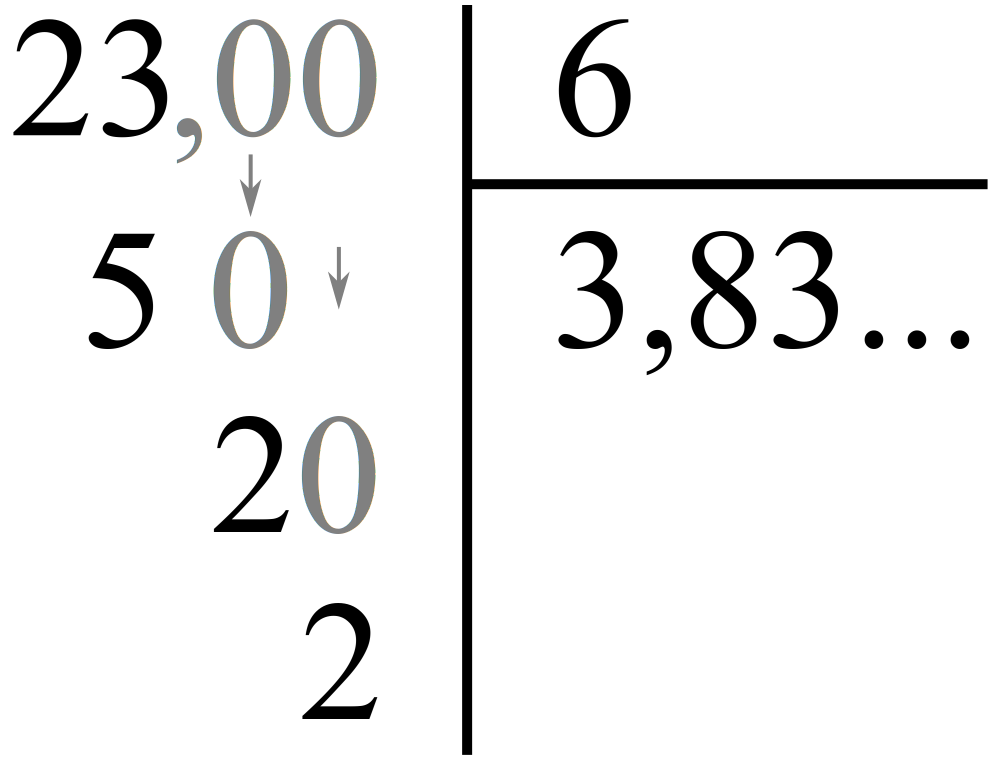
Deux situations peuvent se présenter :
Dans ce dernier cas le quotient n'est pas décimal, on donne généralement un arrondi (ou une valeur approchée - par défaut ou excès - du quotient. )
Un nombre décimal non entier au dividende ne pose pas de problème insurmontable. Plutôt que de "descendre des zéros", on commence par descendre le chiffre des dixièmes, des centièmes , des millièmes : etc...
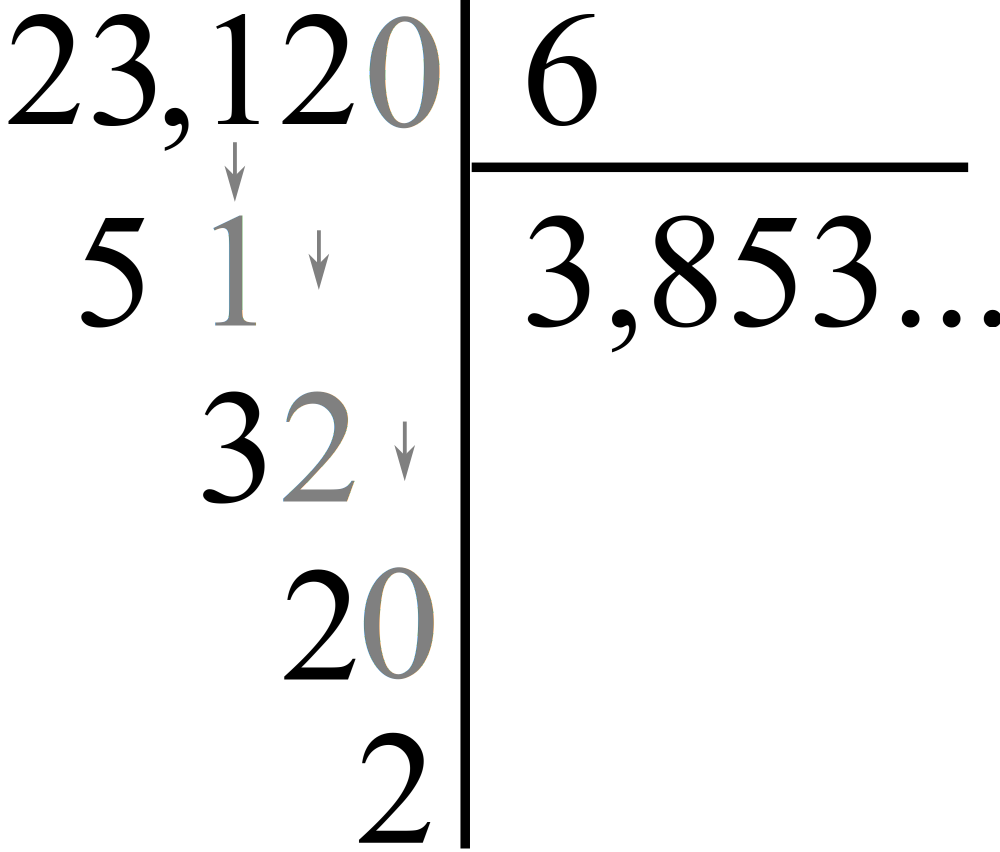
On règle la difficulté du nombre décimal non entier au diviseur en multipliant le dividende et le diviseur par 10, 100, 1000 ... de façon à retrouver un entier naturel.
Par exemple si on cherche le quotient \( \dfrac{2,312}{0,6} \), on remarque que \( \dfrac{2,312}{0,6} = \dfrac{23,12}{6} \approx 3,853 \).
Connaître et mettre en œuvre un algorithme de calcul posé pour effectuer :
Remarque : D'après les instructions officielles, dans le cas de la division, on se limite à diviser par un entier.
Au cycle 1, les nombres entiers sont liés aux objets qu’ils ont servi à dénombrer, puis ils s’en détachent progressivement pour prendre pleinement leur statut de nombres, indépendants des collections.
De la même façon, les fractions sont tout d’abord liées aux partages physiques dont elles rendent compte, avant de s’en détacher progressivement à travers des comparaisons, des rangements, des repérages sur une demi-droite graduée, des calculs, pour prendre pleinement leur statut de nombres. Les nombres que l’on peut écrire sous la forme d’une fraction sont appelés les nombres rationnels.
En dernière année de cycle 3, la fraction \( \dfrac{a}{b} \) , où a est un nombre entier et b est un nombre entier non nul, est définie comme le nombre qui, multiplié par b, donne a.
Un nombre décimal est un nombre qui peut s’écrire sous la forme d’une fraction décimale.
Très progressivement, sur la durée du cycle 3, l’élève apprend ainsi que le nombre décimal qui s’écrit \( \dfrac{318}{100} \) et se dit trois-cent-dix-huit centièmes est aussi trois unités et dix-huit centièmes ou encore trois unités et un dixième et huit centièmes puis s’écrit en respectant le principe de la numération décimale de position : 3,18. Dans l’écriture à virgule des nombres décimaux, la virgule permet de repérer le chiffre des unités.
Utiliser les principes du système décimal de numération et les différentes écritures d’un nombre décimal pour effectuer des calculs, utiliser une droite graduée et modéliser des situations contribuent au développement des langages pour penser et communiquer (domaine 1).
De plus, l’élève, en s’engageant dans une démarche de résolution de problème nécessitant l’utilisation de fractions et/ou de nombres décimaux, en mettant à l'essai plusieurs solutions, en mobilisant les connaissances nécessaires, en analysant et en exploitant les erreurs, développe des méthodes et des outils pour apprendre (domaine 2). L’engagement dans un travail collectif lui permet de développer, dans des situations concrètes, son aptitude à coopérer, à vivre ensemble et à faire preuve de responsabilité (domaine 3).
À l’entrée au cycle 3, les élèves ont déjà rencontré des écritures à virgule à travers l’usage social, dans le contexte des grandeurs (prix, taille, masse, etc.). Les formulations utilisées à l’oral dans la vie courante pour les exprimer, comme « trois euros vingt-cinq » pour 3,25 €, ou « trois mètres vingt- cinq » pour 3,25 m laissent entendre que ces nombres sont conçus comme la juxtaposition de deux entiers plutôt que comme un nombre décimal. En effet, on dit « trois euros vingt-cinq » ou « trois mètres vingt-cinq » tout comme on dit « trois heures vingt-cinq », montrant bien qu’il s’agit là d’une juxtaposition des euros et des centimes d’euros, ou des mètres et des centimètres, comme sont juxtaposées les heures et les minutes. Démarrer l’apprentissage des nombres décimaux en s’appuyant sur cet usage ne favorise de ce fait sans doute pas leur compréhension et risque au contraire d’encourager les élèves à concevoir l’écriture à virgule d’un nombre comme étant composée de deux nombres entiers, juxtaposés et séparés par une virgule.
Les ruptures et continuités énoncées dans le paragraphe précédent expliquent le choix indiqué dans les programmes, de construire les décimaux à partir des fractions décimales, dès le début du cycle 3. Cette construction est un processus progressif qui nécessite du temps et s’organise de façon graduelle selon les étapes déclinées ci-dessous ; il est essentiel que les nouveaux éléments introduits soient explicitement mis en lien avec les éléments préexistants, et que ces derniers continuent de vivre en articulation avec les nouvelles notions.
Pour chacune de ces étapes, le recours à l’oral est privilégié et les écritures symboliques utilisant le trait de fraction et la virgule ne sont introduites qu’une fois le sens construit et non a priori ; le repérage sur une demi-droite graduée est une forme de représentation qui participe à la compréhension des différentes notions travaillées.
