
Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Le temps est un grand maître. Le malheur, c'est qu'il tue ses élèves.



On dit qu'un tableau est un tableau de proportionnalité si les termes de la deuxième ligne s'obtiennent en multipliant ceux de la première par un même nombre. Ce nombre s'appelle le coefficient de proportionnalité.
Exemple:
| Côté d'un carré en cm | 1 | 2 | 3 | 4 | 5 | 10 | 4.1 |
| Périmètre de ce carré en cm | 4 | 8 | 12 | 16 | 20 | 40 | 16.4 |
Ce tableau est un tableau de proportionnalité.
Le coefficient est 4
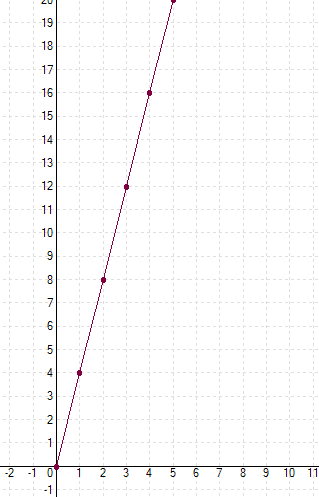
Les points représentés sur le graphique sont alignés avec l'origine du repère.
Le coefficient directeur 4 peut être observé graphiquement :
Lorsque l'on avance de 1 unité sur l'axe des abscisses, on monte de 4 unités sur l'axe des ordonnées.
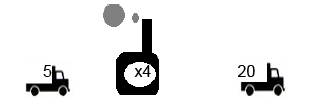
L'usine représente la fonction linéaire f qui à 𝑥 associe 4𝑥.
On note :
f : 𝑥 → 4𝑥 ou f(𝑥) = 4𝑥
On a :
f : 5 → 20 ou f(5) = 20.
L'usine f (la fonction linéaire) transforme la matière première (les nombres) pour « fabriquer » de nouveaux nombres (qu'on appelle images).
f(3) = 12 peut se traduire par :
Par la fonction linéaire f, l'image du nombre 3 est le nombre 12.
Ainsi à chaque situation de proportionnalité correspond une fonction linéaire.
La représentation graphique d'une fonction linéaire est donc une droite passant l'origine du repère.
Un magasin augmente le prix de tous ses produits de 15%, remplir le tableau suivant: Prix avant l'augmentation en euros
| Prix avant l'augmentation en euros | 24.40 | 48.80 | 25 | ||
| Prix après l'augmentation en euros | 28.06 | 1122.4 | 33.12 |

| Prix avant l'augmentation en euros | 24.40 | 48.80 | 976 | 25 | 28.80 |
| Prix après l'augmentation en euros | 28.06 | 56.12 | 1122.4 | 28.75 | 33.12 |
En pratique on peut utiliser la fonction linéaire
g: 𝑥 → 1,15𝑥
pour calculer le nouveau prix après une augmentation de 15%
En effet :
𝑥 + 0,15𝑥 = (1+0,15)𝑥 = 1,15𝑥
On a facilement :
g(100)=115, g(0)=0 etc.
Retrouver un prix avant l'augmentation revient à chercher un antécédent, c'est à dire à diviser par 1,15:
33,12 1,15 = 28,8

D'autres situations classiques de problèmes sont en rapport avec la proportionnalité et les fonctions linéaires:
Penser à la fonction linéaire associée nous fait gagner du temps, pas en perdre !
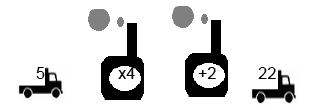
Une fonction affine est un mécanisme qui effectue sur un nombre donné successivement deux travaux:
ici on h: 𝑥 → 4𝑥 + 2 ou ou h( 𝑥 ) = 4𝑥 + 2
par exemple h( 5 ) = 4 × 5 + 2 = 20 + 2 = 22
Une fonction linéaire est une fonction affine particulière:
f: 𝑥 → 4𝑥 peut être vue comme f: 𝑥 → 4𝑥 + 0
A toute fonction affine, on peut associer de manière évidente une unique fonction linéaire :
A l'application affine g: 𝑥 → 3𝑥 + 5 on associe la fonction linéaire g₂: 𝑥 → 3𝑥.
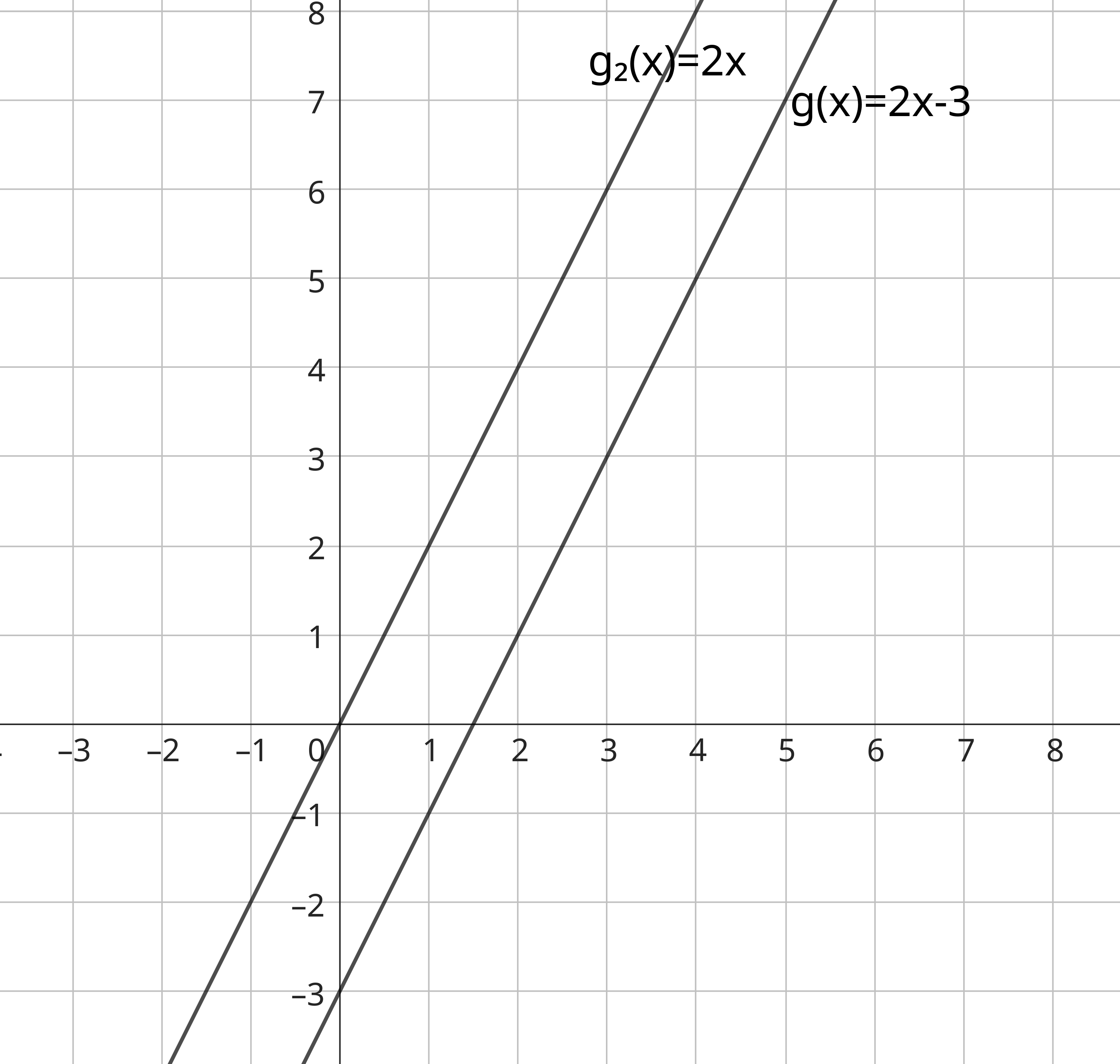
La représentation graphique de la fonction affine g: 𝑥 → 2𝑥 - 3 est une droite qui passe par le point de coordonnées (0 ; -3) appelé ordonnée à l'origine. Son coefficient directeur est 2.
Cette droite est parallèle au graphe de l'application linéaire g₂: 𝑥 → 2𝑥.
Un artisan propose deux tarifs pour la pose de carrelage :
Un client souhaite faire poser une surface de x mètres carrés.

Tarif A : f(𝑥) = 25𝑥
Tarif B : g(𝑥) = 20𝑥 +60
Pour 5 m², on a f(5) = 125 € et g(5) = 60 + 100 = 160 €
Le tarif A est le plus avantageux.
Pour 10 m², on a f(10) = 250 € et g(10) = 60 + 200 = 260 €
Le tarif A est encore le plus avantageux.
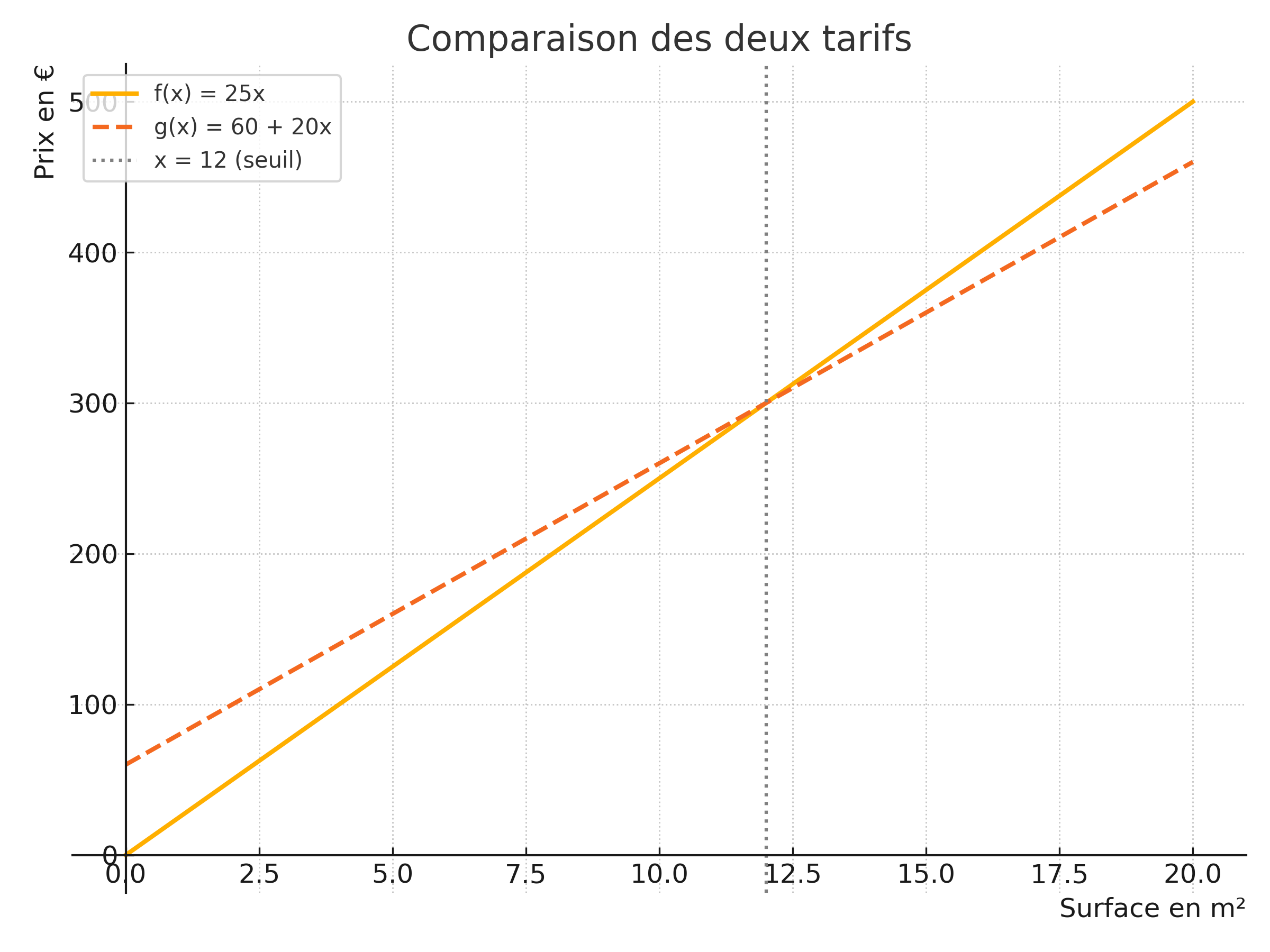
Pour savoir quand le tarif B devient plus avantageux que le tarif A, on résout l'inéquation suivante :
60 + 20x < 25x
60 < 5x
x > 12
Le tarif B devient plus avantageux au dessus de 12 m².

x → ax et x → ax + b pour des valeurs numériques fixéesLa fonction linéaire s’appuie sur les notions de proportionnalité : multiplier par un coefficient a. On utilisera des tableaux de proportionnalité, des pourcentages (ex : +5% ⇨ ×1,05), et la représentation graphique (droite passant par l’origine).
On introduit la notation x → ax, et on interprète graphiquement le coefficient directeur a.
La fonction affine, de la forme x → ax + b, s’obtient par une translation de la fonction linéaire. Le coefficient a et l’ordonnée à l’origine b sont à interpréter graphiquement. On exploite deux points du graphique pour déterminer cette fonction affine.
Il est utile de confronter les fonctions linéaires et affines à d’autres formes de fonctions (ex : x²) pour distinguer les cas particuliers.
La classe de 3e constitue le premier contact formel avec la notion de fonction. On évite toutefois une définition trop générale. L’accent est mis sur les fonctions linéaires et affines, en lien avec la proportionnalité, les grandeurs, et les représentations graphiques.
Les élèves sont amenés à passer d’un langage à un autre : formule, tableau, graphique. C’est l’occasion d’introduire les notations f(x), de distinguer les parenthèses dans ce contexte et d’interpréter les lettres comme variables ou constantes.
On veillera à préciser le domaine d’utilisation d’une fonction dans une situation réelle (par exemple, restreint à un intervalle).
La fonction linéaire est un cas particulier de la fonction affine, souvent rencontrée dans des problèmes de tarifs, de coûts, ou de proportions. Elle sert aussi à modéliser des situations concrètes dans d’autres disciplines (physique, chimie, éco-droit…).

Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager :