Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Même si vous jouez la perfection, une faute de votre adversaire peut détruire toute la beauté de la partie.
Vladimir Kramnik ( Nouveau design ! )
Dans cette leçon, nous allons découvrir comment repérer des points sur une droite graduée, puis dans un repère du plan.
Le point I a deux utilités : la longueur OI définit l'unité de la droite, et on gradue la droite à partir de O en direction de I, comme sur l'image ci-dessus.
On place traditionnellement I à droite de O. Pourquoi ? Parce que nous lisons de gauche à droite. Ainsi, à gauche de O se trouvent les nombres négatifs (précédés d’un "−") et à droite les nombres positifs (écrits avec un "+" ou sans signe).
Ces nombres (positifs et négatifs) sont appelés nombres relatifs.
Zéro est le seul nombre relatif à la fois positif et négatif...
0 = +0 = -0
(oui, égal... la tête à Toto)
Ainsi, sur une droite graduée, tout point est repéré par un nombre relatif : son abscisse.
Plaçons sur cette droite graduée le point A d'abscisse 4 :
Plaçons maintenant le point B d'abscisse -3 :
Dans les exemples précédents, le segment [OA] mesure 4 unités et [OB] mesure 3 unités.
Autrement dit : la distance du point A à O est 4, celle du point B à O est 3.
On peut exprimer cela en utilisant les abscisses :
La distance à zéro est toujours positive !
Pour trouver la distance à zéro d’un nombre relatif, il suffit d’« oublier » son signe.
On appelle nombres relatifs opposés deux nombres de même distance à zéro mais de signes contraires.
Place sur cette droite les points A' et B' ayant pour abscisses les opposés de ceux des points A et B.
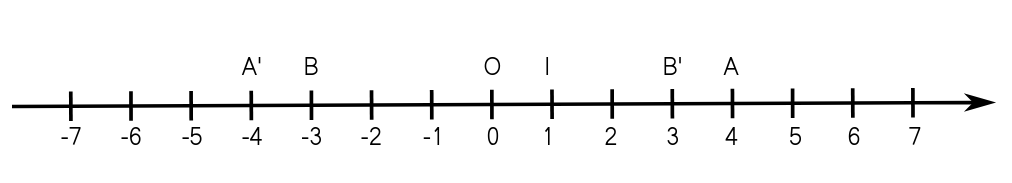
Sur une droite graduée (I à droite de O), les abscisses sont dans l’ordre croissant. Plus un point est à gauche, plus son abscisse est petite ; plus il est à droite, plus son abscisse est grande.
-4 < -3 < 0 < 1 < 3 < 4
Propriété 1 : De deux nombres relatifs de signes contraires, le plus grand est le positif.
-3 < 4
Propriété 2 : Deux nombres positifs sont rangés selon leur distance à zéro.
3 < 4
Plus un nombre positif est proche de zéro, plus il est petit.
Propriété 3 : Deux nombres négatifs sont rangés dans l’ordre inverse de leur distance à zéro.
-4 < -3
Plus un nombre négatif est proche de zéro, plus il est grand.
Imagine une carte au trésor ! Pour trouver le trésor, tu as besoin de deux informations : combien de pas aller à droite ou à gauche (l’abscisse), et combien de pas aller en haut ou en bas (l’ordonnée).
Un repère du plan, c’est un peu comme une carte. Il te permet de situer un point sur une feuille.
À partir de l’origine O :
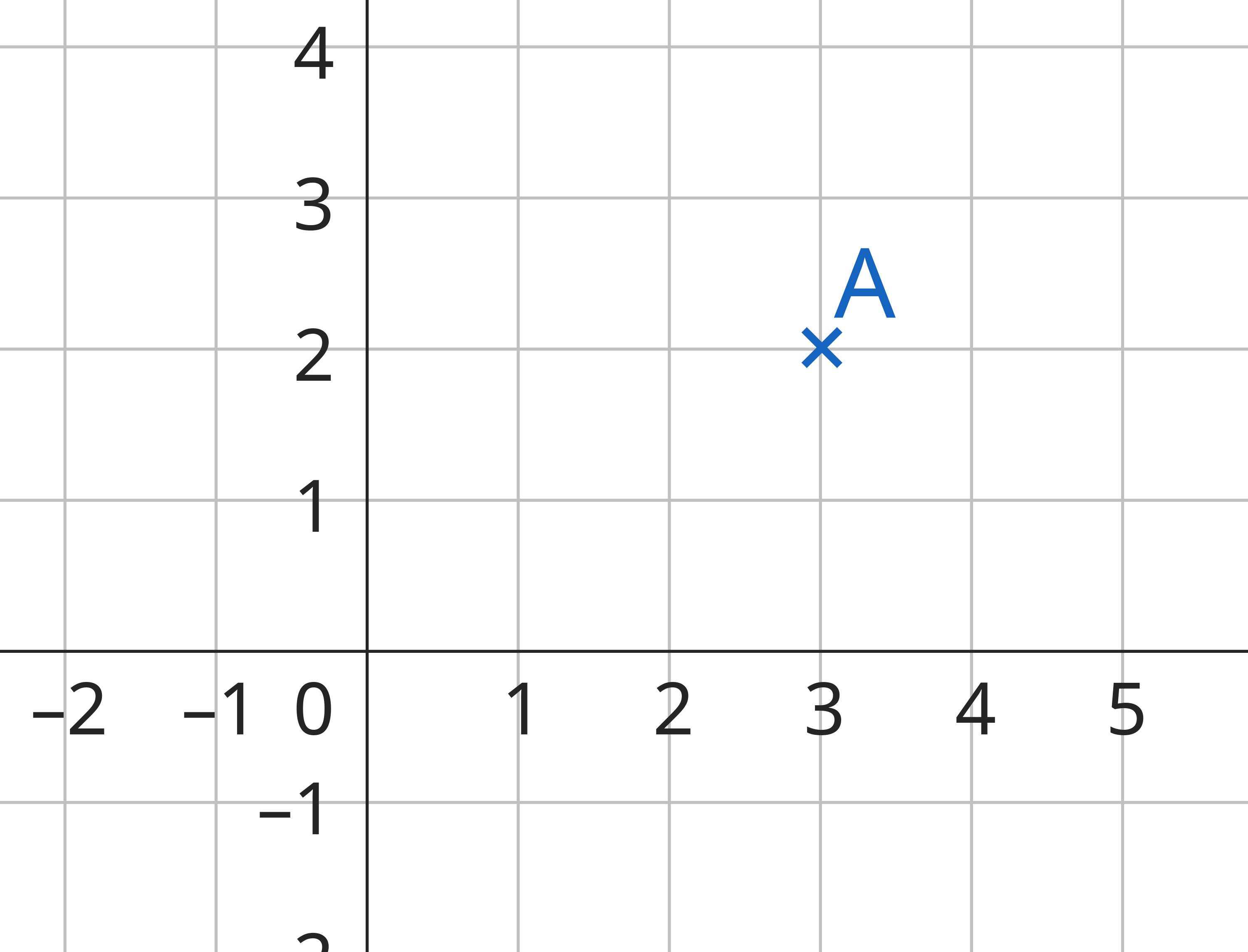
On note alors la position du trésor : A (3 ; 2)
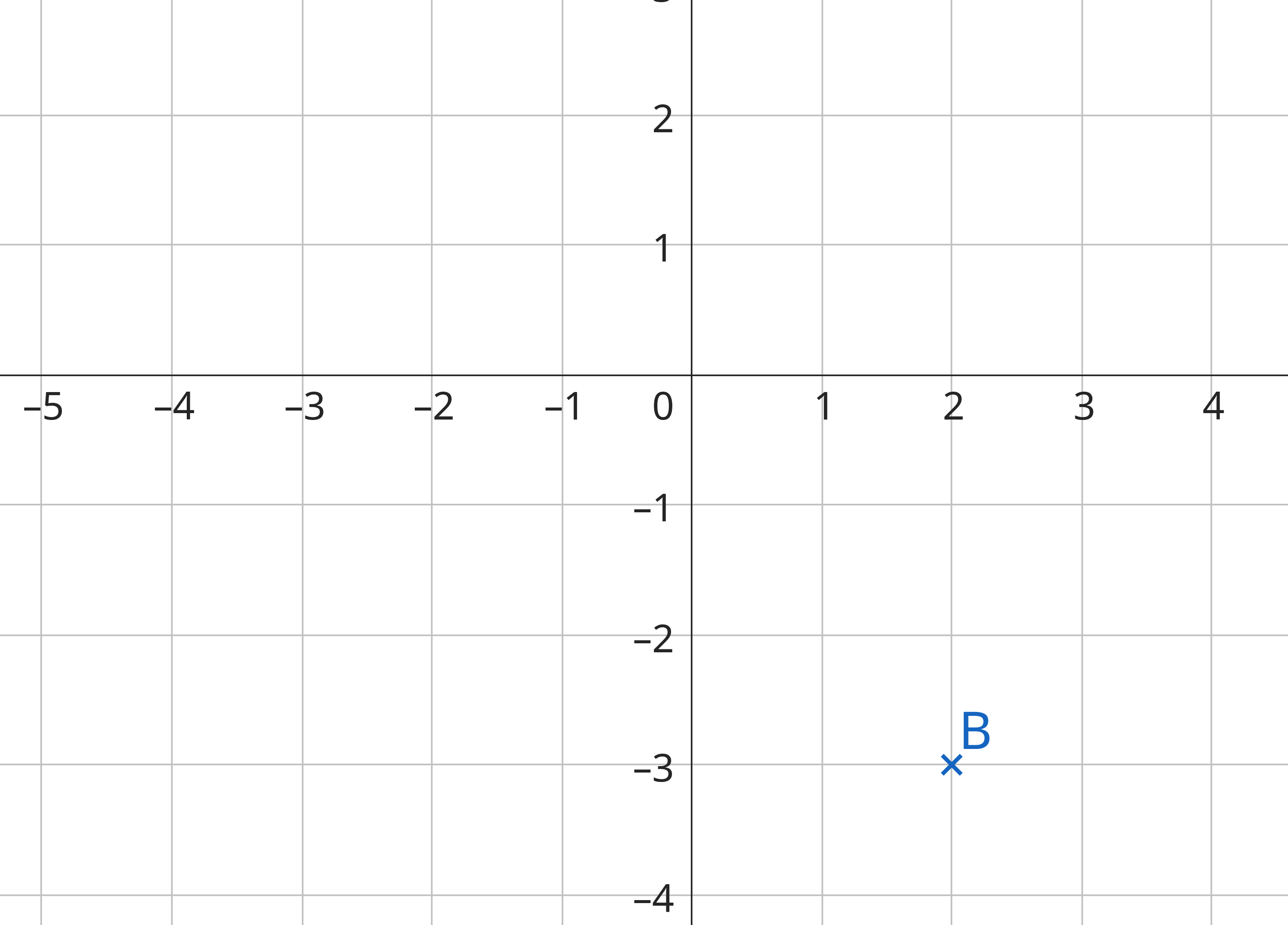
La position du trésor est : B (2 ; -3)
Un repère orthogonal du plan est composé de deux droites graduées perpendiculaires, ayant le même point d’origine. L’axe horizontal est l’axe des abscisses, et l’axe vertical est l’axe des ordonnées.
Chaque point est repéré par deux nombres appelés coordonnées : l’abscisse (x) et l’ordonnée (y).
Deux points ayant la même abscisse sont sur une même droite verticale.
Deux points ayant la même ordonnée sont sur une même droite horizontale.
Ce chapitre s’inscrit dans le domaine « Espace et géométrie » du cycle 4. Il vise principalement l’attendu suivant du programme de mathématiques : « Utiliser un système de coordonnées pour repérer des points, des objets, décrire des situations ou des déplacements ». Il permet de consolider la maîtrise du repérage sur une droite graduée et dans un repère orthogonal, en mobilisant la compréhension des nombres relatifs et des coordonnées cartésiennes.
Cette séquence contribue à plusieurs compétences du socle commun, notamment :
Sur le plan pédagogique, la révision du repérage sur une droite graduée renforce la notion de distance et d’opposés, utile notamment pour aborder la symétrie centrale ou encore les translations. Il est pertinent d’introduire ou de réactiver les repères dans des contextes variés (cartographie, déplacements, codage). Des activités numériques peuvent être proposées avec des outils comme GeoGebra ou en lien avec le site Eduscol pour diversifier les approches.
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: