Aire et périmètre

I. Le polygone quelconque

1. Périmètre d'un polygone quelconque

Définition

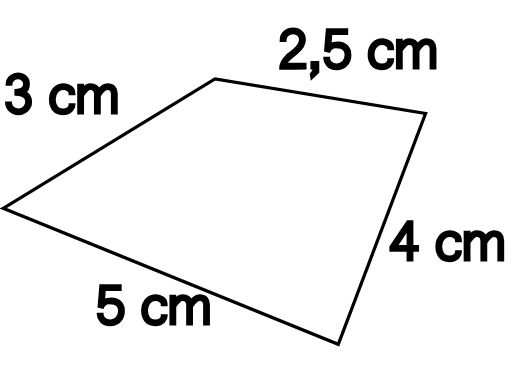
Le périmètre d’une figure est la longueur de son contour.

On imagine une fourmis qui fait le tour du polygone en calculant sa distance parcourue:

Ici on a P = 5 + 4 + 2,5 + 3 = 14,5 cm

B. Aire d'un polygone quelconque

On ne dispose pas de formule pour calculer l'aire d'un polygone quelconque !

II. Le carré

1. Périmètre d'un carré

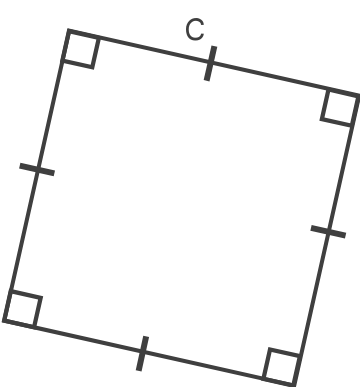
Le périmètre d'un carré de côté c est donné par la formule suivante :

P = 4 × c

Un carré de côté 5 cm a donc un périmètre de 4 × 5 = 20 cm

2. Aire d'un carré

L'aire d'un carré de côté c est donnée par la formule suivante :

A = c × c

Un carré de coté 5cm a donc une aire de 5 × 5 = 25 cm²

III. Le rectangle

A. Périmètre d'un rectangle

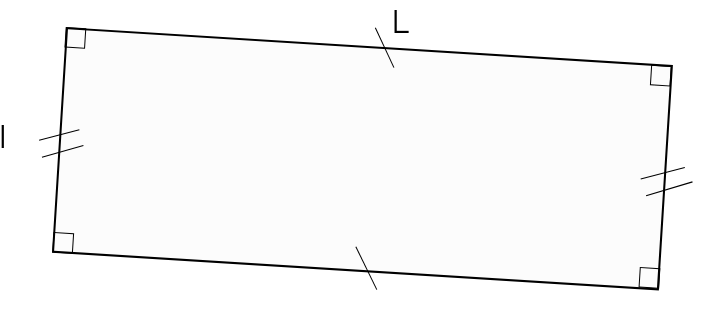
Le périmètre d'un rectangle de longueur L et de largeur l est donné par la formule suivante :

P = 2 × (L + l) =2 × L + 2 × l

Ainsi, si on a un rectangle de longueur 7m et de largeur 3m, son périmètre est :

2 × (7 + 3) = 2 × 10 = 20 m

ou

2 × 7 + 2 × 3 = 14 + 6 = 20 m

B. Aire d'un rectangle

L'aire d'un rectangle de longueur L et de largeur l est donnée par la formule suivante :

A = L × l

Ainsi, si on a un rectangle de longueur 7 m et de largeur 3 m, son aire est :

7 × 3 = 21 m²

IV. Le triangle rectangle

A. Périmètre d'un triangle rectangle

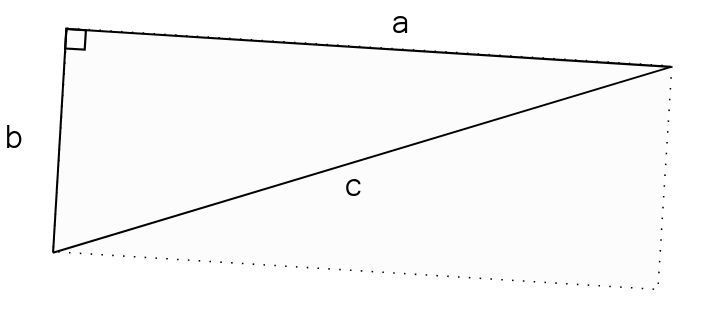
Le périmètre se calcule comme pour tous les polygones quelconques (penser à la fourmis) en ajoutant les mesures des segments qui le composent:

Ici on a:

P = a + b + c

Ici, si a,b et c sont respectivement égaux à 4 km, 3 km et 5 km, le périmètre du triangle est :

P = 4 + 3 + 5 = 12 km

B. Aire d'un triangle rectangle

L'aire d'un triangle rectangle dont les côtés de l'angle droit ont pour mesures a et b est donnée par la formule suivante :

A = a × b 2

Ici, si a,b et c sont respectivement égaux à 4 km, 3 km et 5 km, l'aire du triangle est :

A = 4 × 3 2 = 6 km²

V. Le triangle quelconque

A. Vocabulaire important

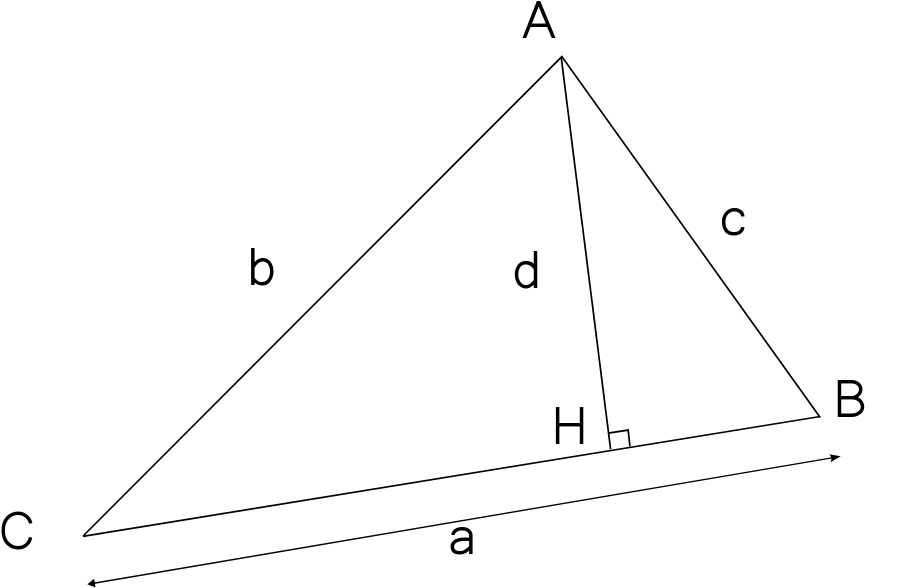
Dans le triangle quelconque ci-dessus (AH) ⊥ (BC) . On dit que :

[AH] est la hauteur issue de A.

ou que

[AH] est la hauteur relative au coté [BC].

Le point H est appelé :

pied de la hauteur.

B. Périmètre d'un triangle

Le périmètre se calcule comme pour tous les polygones quelconques en ajoutant les mesures des segments qui le composent:

Ici on a:

P = a + b + c

C. Aire d'un triangle

L'aire d'un triangle est égale à la moitié du produit de la longueur d'un côté par sa hauteur relative.

Ici on a :

A = a × d 2

Quand il y a un angle obtus dans le triangle, le pied de la hauteur peut se situer hors du segment :

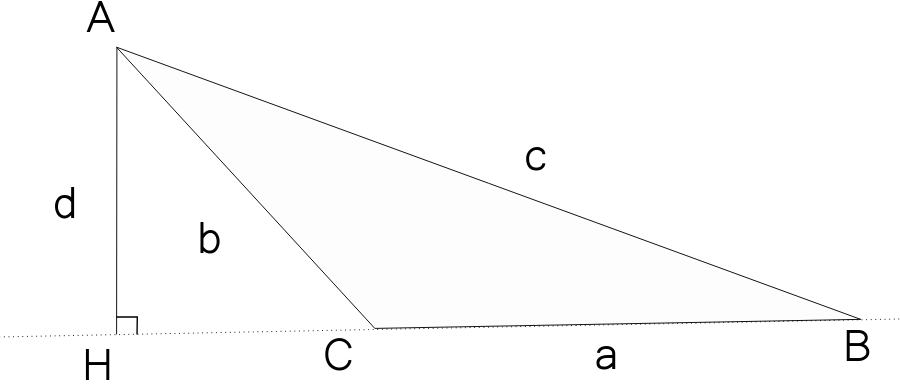
Mais cela ne change aux formules:

P = a + b + c

et

A = a × d 2

VI. Le cercle, le disque

A. Définition : Le cercle

Le cercle de centre O et de rayon 5cm (par exemple) est l'ensemble des points situés à 5cm de O.

5cm est le rayon du cercle.

B. Définition : Le disque

Le disque de centre O et de rayon 5cm (par exemple) est l'ensemble des points situés à moins de 5cm de O.

5cm est le rayon du disque.

C. Un peu de vocabulaire

• Le point O est le centre du cercle, c'est aussi le centre du disque.
• Les segments [OA], [OB] et [OC] sont des rayons du cercle (et du disque.)
• La longueur OA= OB = OC est le rayon du cercle (et du disque.)
• Le segment [AB] est un diamètre du cercle (et du disque.)
• La longueur AB est le diamètre du cercle (et du disque.)
• Le segment [BC] (pas tracé), qui joint deux points distincts du cercle, est une corde du cercle (et du disque.)
• Le diamètre [AB] est la plus grande corde du cercle (et du disque.)
• La partie du cercle entre B et C est un arc de cercle et se note :BC

D. Aire et périmètre

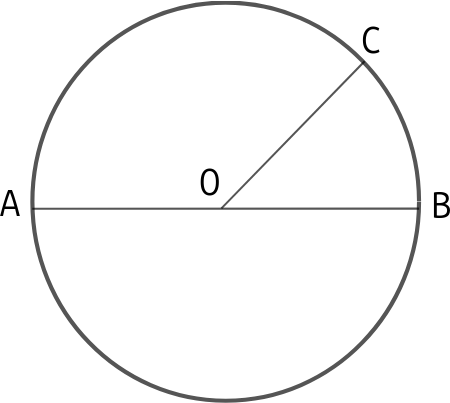
Même si ces deux objets se ressemblent, ils sont très différents. On parlera du périmètre d'un cercle et de l'aire d'un disque.

0. Parlons π (pi)

Le nombre π (pi) est un nombre très célèbre en mathématiques. On le retrouve dès qu’on travaille avec des objets de formes circulaires. Il est un peu mystérieux, car c’est un nombre infini, qui ne s’écrit jamais complètement. Il commence par 3,14, mais il continue sans jamais s’arrêter ni former de boucle. Les mathématiciens l’utilisent depuis très longtemps, et il apparaît dans plein de formules quand on parle de cercles, de disques...

1. Périmètre de ce cercle.

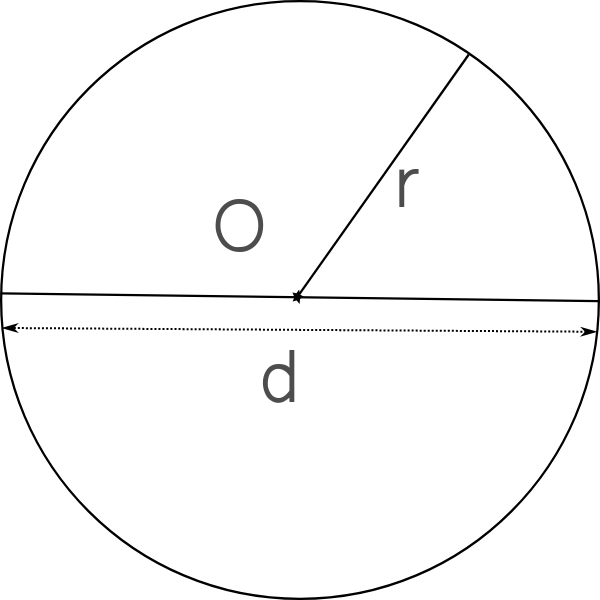
Le périmètre de ce cercle de centre O, de rayon r et de diamètre d est donné par la formule :

P = 2 × π × r = π × d

2. Aire de ce disque.

L'aire de ce disque, de rayon r et de diamètre d est donné par la formule :

A = π × r × r = π × r²

Fiche mémo

Voici un résumé des formules d’aire et de périmètre pour les principales figures étudiées :

Toujours indiquer les unités dans tes résultats : m, cm, m², cm²…

Un cahier d'exercices de 128 pages ...

Le cahier : 5,40 €

Plus de Produits