Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
L'homme est le seul animal qui rougisse ; c'est d'ailleurs le seul animal qui ait à rougir de quelque chose.
Les mots comme somme, produit, double, tiers… vous disent quelque chose ? Êtes-vous capables de les comprendre et de les utiliser dans des calculs ?
Traduire les expressions suivantes en langage naturel :
La procédure inverse consiste à écrire l'expression littérale d'après l'expression en langage naturel.
Exemple 1 : Écrire le produit de 7 par la somme de π et 3 2
Exemple 2 : Écrire la somme de 7 et du produit de π par 3 2
Exemple 1 : Écrire le produit de 7 par la somme de π et 3 2
7 ( π + 3 2 )
Vous avez oublié les parenthèses ?
C'est une erreur : Vous avez écrit la somme du produit de 7 par π et 3 2
Exemple 2 : Écrire la somme de 7 et du produit de π par 3 2
7 + π × 3 2 = 7 + π × 3 2 = 7 + 3π 2
Vous avez ajouté des parenthèses ?
7 + (π × 3 2 )
C'est une imperfection ! Si on se souvient des priorités opératoires, les parenthèses ne servent à rien !
Cet objectif vise à établir un lien clair entre le langage mathématique formel et son interprétation verbale
L’élève comprend la signification des symboles +, ×, puissances, parenthèses. Il parvient à formuler en français des expressions simples à modérées.
2,5 × 4,36 + 7,5 × 4,36
Cette expression est une somme de produit.
en effet en "pensant priorités opératoires" on a:
(2,5 × 4,36) + (7,5 × 4,36)
Regardons attentivement les deux produits.
Le premier est constitué de deux facteurs 2,5 et 4,36
Le deuxième est constitué de deux facteurs 7,5 et 4,36
4,36 est un facteur commun et on a :
2,5 × 4,36 + 7,5 × 4,36 = 4,36 × (2,5 + 7,5)
On vient de transformer une somme en produit ! On avait des termes, maintenant on a des facteurs. On a factorisé.
Et on peut terminer le calcul :
2,5 × 4,36 + 7,5 × 4,36 = 4,36 × (2,5 + 7,5) = 4,36 × 10 = 43,6
3π + 5π + 2π
À nouveau on a une expression du type somme, cette fois-ci de trois produits, avec le nombre π en facteur commun.
On a :
3π + 5π + 2π = π × ( 3 + 5 + 2 ) = π × 10 = 10π ≈ 31,4
L'égalité suivante est toujours vraie pour tous les nombres a,b et k :
ka + kb = k(a+b)
De la gauche vers la droite on dit qu'on factorise k
Identifier un facteur commun dans une somme de termes et transformer cette somme en un produit. Utiliser cette transformation pour simplifier des calculs ou manipuler des expressions littérales.
L’élève reconnaît les situations où une factorisation est possible, y compris dans des expressions numériques. Il sait isoler le facteur commun et reformuler l’expression.
La formule qu'on vient de voir va nous permettre de réduire certaines sommes algébriques :
3a+ 2b+ 5a =On a une somme de trois termes 3a, 2b et 5a. L'ordre n'importe pas...
3a + 5a + 2b = On factorise a
a(3+5) + 2b = a × 8 + 2b =
8a + 2b
Ici, on ne peut rien faire. On n'a aucun facteur commun aux trois produits.
Celle-ci embête les élèves comme "il n' y a pas de nombre devant le t"... jusqu'à ce qu'on explique que t = 1 × t =1t
7t + 2u + t =
7t + 2u + 1t =
7t + 1t + 2u =
(7 + 1)t + 2u = 8t + 2u
Ici ce sont les "-" qui embêtent les élèves.
En fait on a une somme de 4 termes -2a, 3b, 2a et -2b qu'on pourrait écrire :
-2a + 3b + 2a + (-2b)
On peut changer l'ordre des termes et regrouper ceux de son choix :
-2a + 3b + 2a - 2b = a(-2 +2) + b(3 -2) = 0 × a + 1 × b = b
On additionne ou on soustrait les coefficients et on écrit le résultat.
Par abus de langage on dit qu'on compte les a, les a², les b...
Pour ne pas oublier de lettre (avec exposant) on peut prendre les exposants par ordre décroissant et les lettres par ordre alphabétique :
L'expression réduite est donc 6a² - 3a - 2b
Reconnaître les termes semblables, les regrouper et effectuer les calculs nécessaires pour simplifier une expression littérale. Utiliser la réduction pour faciliter l’écriture et la résolution d’équations.
L’élève parvient à identifier les termes de même nature et à les combiner. L’automatisation est encore en cours.
3(5+3a) + 2a est une somme algébrique qu'il semble impossible de réduire à cause des parenthèses...
L'égalité suivante est toujours vraie pour tous les nombres a,b et k :
ka + kb = k(a+b)
De la gauche vers la droite on dit qu'on factorise k
De la droite vers la gauche on dit qu'on distribue k, ou qu'on développe (étymologie : on enlève l'enveloppe.)
Commençons par développer (distribuer 3)
3(5+3a) + 2a =
3 ×5 + 3 ×3a +2a =
15 + 9a +2a =
11a + 15
La consigne "Développer, réduire et ordonner" est une instruction courante en algèbre, particulièrement lorsqu'on travaille avec des expressions littérales. Elle regroupe trois étapes successives pour simplifier une expression mathématique.
C'est l'opération contraire de la factorisation. Elle consiste à supprimer les parenthèses en appliquant la distributivité.
Exemple: Développer l'expression 3(a+2) revient à écrire 3a + 6.
Une fois les parenthèses supprimées, on regroupe les termes semblables. Les termes semblables sont ceux qui ont la même partie littérale (les mêmes lettres avec les mêmes exposants).
Exemple: Dans l'expression 3a + 2b + a - b, on regroupe les termes en a (3a et a) et les termes en b (2b et -b) pour obtenir 4a + b.
Cette étape est optionnelle mais recommandée. Elle consiste à écrire les termes de l'expression dans un ordre précis, généralement par ordre décroissant des puissances d'une lettre choisie.
Exemple: On écrira souvent l'expression 3 - 2c² + c³ comme ceci: c³ - 2c² + 3
Appliquer la propriété distributive pour transformer un produit en une somme. Maîtriser cette transformation dans des expressions du type a(b + c)
L’élève applique correctement la distributivité et sait développer une expression simple. Il utilise cette compétence pour préparer une réduction ou résoudre une équation.
Le signe égal, bien qu'il puisse sembler simple, renferme une richesse de sens en mathématiques.
Il ne signifie pas toujours "faire" comme sur une calculatrice.
En algèbre, il exprime une égalité entre deux expressions, qu'elles soient numériques ou littérales.
C'est un outil puissant pour poser des problèmes (équations), pour vérifier des résultats, pour exprimer des relations (formules).
Parfois, il sert à affecter une valeur à une inconnue, comme dans une affectation informatique.
Il est donc essentiel de comprendre le contexte dans lequel il est utilisé pour ne pas commettre d'erreurs.
Le signe "=" n'a pas toujours le même sens !
Une égalité est une affirmation qui indique que deux expressions ont la même valeur. On la représente par le signe égal.
Pour x=10 cette dernière égalité est fausse : 2×10 + 5 = 20 + 5 = 25 et 25 ≠ 11
P = 2πR est une formule qui nous rappelle ce qu'il faut faire pour calculer le périmètre d'un cercle...
Une équation est une égalité mathématique qui contient au moins une inconnue.
Résoudre une équation c'est trouver toutes les valeurs de l'inconnue qui rendent l'égalité vraie.
On a vu tout à l'heure que 2x + 5 = 11 est une égalité. (fausse pour x=10)
x étant une inconnue, cette égalité est une équation. Équation que nous allons résoudre.
2x + 5 = 11
2x + 5 - 5 = 11 - 5
2x = 6
2x 2 = 6 2
x = 3
Cette équation admet une unique solution
En testant cette valeur tout à l'heure on aurait pu conclure que 3 était une solution, mais nous n'étions pas certain que c'était la seule !
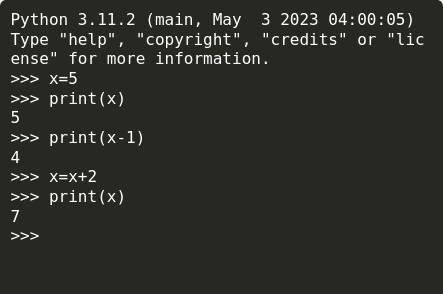
En programmation (Python dans l'image ci-dessus) le code x=5 n'est pas une égalité mais une affectation.
Dans certain langage pour éviter cette ambiguïté on notera plutôt : x ← 5
L'affectation sert à attribuer une valeur à une variable. C'est comme si on mettait un étiquette sur une boîte : l'étiquette (la variable) correspond au contenu de la boîte (la valeur).
Ici, on affecte la valeur 5 à la variable x. Après cette instruction, chaque fois qu'on rencontrera x dans le programme, il sera remplacé par 5.
Le code : print(x) demande simplement à Python d'imprimer à l'écran la valeur de la variable x.
Ce qui est plus étonnant c'est que quand on écrit maintenant x=x+2, on affecte à la variable x une nouvelle valeur 5 + 2 soit 7. Vous pouvez-vous amuser avec l'affectation avec le bac à sable Python du site2wouf.fr
Dans un tableur (comme Excel ou LibreOffice Calc), le signe égal = est utilisé pour commencer une formule de calcul.
Par exemple, si l'on saisit =A1+B1 dans une cellule, le tableur additionnera les valeurs contenues dans les cellules A1 et B1.
Attention : ici, le signe = n’exprime pas une égalité au sens mathématique classique, mais indique que la cellule doit afficher le résultat d’un calcul. Dans un tableur, toute formule commence par le signe =
Faire la distinction entre une égalité de calcul, une définition, et une transformation d'expression. Utiliser le signe égal à bon escient selon le contexte.
L’élève repère que « = » peut signifier des choses différentes. Il commence à justifier ses transformations en précisant ce que l’égalité exprime (valeur, équivalence, étape de calcul).
🎯 Compétence : Comprendre et traduire une expression littérale en langage courant.
📌 Description : Formuler en français une expression du type 3x + 1. Faire le lien entre une écriture symbolique et sa signification dans une situation simple.
📚 Source : Programme cycle 4 — Domaine : Calcul littéral
🎯 Compétence : Reconnaître un facteur commun et transformer une somme en produit.
📌 Description : Savoir extraire un facteur commun dans des expressions simples du type 3x + 6. Utiliser cette transformation pour simplifier un calcul.
📚 Source : Programme cycle 4 — Manipuler une expression littérale
🎯 Compétence : Identifier et regrouper les termes de même nature.
📌 Description : Simplifier une expression comme 3x + 4x – 2. Reconnaître que les termes doivent avoir la même partie littérale pour être regroupés.
📚 Source : Programme cycle 4 — Transformer une expression littérale
🎯 Compétence : Appliquer la distributivité simple ou double.
📌 Description : Transformer une expression factorisée comme 3(x + 2) en une somme. Savoir appliquer (a + b)(c + d) dans des cas guidés.
📚 Source : Programme cycle 4 — Développer une expression littérale
🎯 Compétence : Différencier les usages du signe égal.
📌 Description : Comprendre qu’« = » peut exprimer une définition, une équivalence ou un résultat. Utiliser ce signe à bon escient dans une démarche de calcul ou de preuve.
📚 Source : Programme cycle 4 — Raisonnement / Calcul littéral
Le Cahier numérique iParcours Maths 5e avec cours est un logiciel qui permet d'afficher et de projeter le Cahier d'exercices iParcours 5e (éd. 2022) en version numérique.
La clé USB : 49,00 €
Partager: