Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Il ne faut jamais faire que les sottises qui nous plaisent.
🔑 Code de cette page :
Lorsque l’on réalise une enquête, on est amené à étudier des caractères propres à chaque individu. L’ensemble des individus est appelé la population.
Le caractère peut être qualitatif (la couleur des cheveux, les sports pratiqués, le type de film préféré) ou quantitatif (la taille, l’âge, le temps passé devant la télévision).
L’ensemble des données collectées s’appelle une série statistique. Avant traitement, elle est appelée série brute.
Le nombre total d’individus de la population est appelé effectif total de la série. Le nombre d’individus qui possèdent un même caractère est appelé effectif du caractère.
La fréquence d’une valeur est le quotient : effectif de la valeureffectif totaleffectif de la valeur/effectif total Elle peut être exprimée sous forme décimale (exacte ou approchée) ou fractionnaire. C’est un nombre compris entre 0 et 1.
La fréquence en pourcentage est l’écriture de la fréquence sous forme de pourcentage : effectif de la valeureffectif totaleffectif de la valeur/effectif total × 100
Un tableau permet de regrouper et d’organiser des données, de lire et d’interpréter facilement des informations.
Si on étudie un caractère quantitatif, on peut regrouper les données par classes pour limiter la taille du tableau. On détermine alors les effectifs de chaque classe.
Voici les résultats au lancer de javelot lors d’un championnat d’athlétisme. Les longueurs sont exprimées en mètres :
36 42 37 43 38 44 32 40 44 36 46 39 40 40 41 41 45 37 43 43 46 39 44 47 48
1. Compléter le tableau suivant.
| Longueur \(\ell\) du lancer (en mètres) | \(30 \leq \ell < 35\) | \(35 \leq \ell < 40\) | \(40 \leq \ell < 45\) | \(45 \leq \ell < 50\) | Total |
|---|---|---|---|---|---|
| Nombre de sportifs | |||||
| Fréquence | |||||
| Fréquence en pourcentage |
2. Quel est le pourcentage de sportifs ayant lancé au moins à 40 mètres ?
Correction.
| Longueur \(\ell\) (m) | \(30 \leq \ell < 35\) | \(35 \leq \ell < 40\) | \(40 \leq \ell < 45\) | \(45 \leq \ell < 50\) | Total |
|---|---|---|---|---|---|
| Nombre de sportifs | 1 | 6 | 12 | 6 | 25 |
| Fréquence | 0,04 | 0,24 | 0,48 | 0,24 | 1 |
| Fréquence en % | 4 % | 24 % | 48 % | 24 % | 100 % |
Il suffit d’additionner les pourcentages des deux dernières classes :
48 + 24 = 72
Le pourcentage de sportifs ayant lancé au moins à 40 mètres est 72 %.
Dans un diagramme circulaire (ou semi-circulaire), les mesures des angles au centre sont proportionnelles aux quantités représentées. Dans un diagramme en barres (ou en bâtons), les hauteurs des bâtons sont proportionnelles aux quantités représentées.
Pour représenter une situation, il existe plusieurs types de représentations :
le graphique, qui montre les évolutions ;
le diagramme circulaire, qui montre les proportions ;
le diagramme en barres (ou en bâtons), qui montre les répartitions ;
l’histogramme, pour les séries regroupées en classes.
Représente les données du lancer de javelot sous la forme d’un histogramme.
Correction.
Si x_1, x_2, …, x_p représentent les valeurs du caractère de la série et M la moyenne, on a alors : M = x_1 + x_2 + … + x_ppx_1 + x_2 + … + x_p/p
Si les données sont regroupées par classe, on choisit une valeur de l’intervalle pour effectuer le calcul de la moyenne. Classiquement, on prend la valeur centrale de la classe.
En utilisant les valeurs centrales des classes (32,5 ; 37,5 ; 42,5 ; 47,5), calculer la longueur moyenne d’un lancer.
Correction. La longueur moyenne (estimée) du lancer est :
M = 1 × 32,5 + 6 × 37,5 + 12 × 42,5 + 6 × 47,5251 × 32,5 + 6 × 37,5 + 12 × 42,5 + 6 × 47,5/25
M = 1 052,5251 052,5/25 = 42,1 m
La médiane m d’une série dont les valeurs sont ordonnées est la plus petite valeur telle qu’il y ait au moins la moitié de l’effectif inférieur à cette valeur.
L’étendue d’une série est la différence entre la plus grande et la plus petite des valeurs prises par cette série.
À partir des 25 lancers de javelot : quel est le lancer médian ? Quelle est l’étendue ?
Correction. Il y a 25 lancers, donc la médiane est la 13e valeur lorsque les données sont rangées par ordre croissant.
32, 36, 36, 37, 37, 38, 39, 39, 40, 40, 40, 41, 41, 42, 43, 43, 43, 43, 44, 44, 44, 45, 46, 46, 47, 48
La 13e valeur est 41 : le lancer médian est 41 m. L’étendue est :
48 − 32 = 16 m
Les probabilités sont une branche des mathématiques qui s’intéresse à quantifier l’incertitude liée à des événements futurs. Elles nous permettent d’évaluer la chance qu’un événement particulier se produise.
Les statistiques décrivent des données existantes et identifient des tendances ; les probabilités modélisent le hasard. En les combinant, on peut décrire des données, prédire des événements futurs et prendre des décisions en tenant compte de l’incertitude.
Une expérience aléatoire est une expérience qu’on peut répéter, dont le résultat ne peut être prédit avec certitude avant sa réalisation, même si l’ensemble des résultats possibles est connu.
Par exemple : lancer un dé, tirer une carte dans un jeu de 52 cartes, lancer une pièce.
Une issue est tout résultat possible d’une expérience aléatoire. C’est le résultat concret que l’on obtient lorsqu’on réalise une fois l’expérience.
Lancer un dé à six faces : les issues possibles sont 1, 2, 3, 4, 5 ou 6.
Tirer une carte dans un jeu de 52 cartes : chaque carte est une issue différente.
Lancer une pièce : les issues possibles sont pile ou face.
Un événement d’une expérience aléatoire est un regroupement de plusieurs issues qui nous intéresse particulièrement.
Dé : l’événement « obtenir un nombre pair » est composé de 3 issues (2, 4 et 6).
Cartes : l’événement « obtenir un roi » est composé de 4 issues.
Pièce : l’événement « obtenir pile » est composé d’une seule issue.
Un événement qui ne contient qu’une seule issue est appelé événement élémentaire.
La probabilité d’un événement est une mesure numérique qui exprime la chance que cet événement se produise. Elle est comprise entre 0 et 1 :
0 : l’événement est impossible (il ne se produira jamais) ;
1 : l’événement est certain (il se produira à coup sûr) ;
entre 0 et 1 : l’événement est incertain, et la valeur indique sa vraisemblance.
L’équiprobabilité décrit une situation où toutes les issues d’une expérience aléatoire ont exactement la même chance de se produire.
On ne s’intéressera cette année qu’aux expériences aléatoires en situation d’équiprobabilité.
En cas d’équiprobabilité, la probabilité d’un événement est égale au quotient du nombre d’issues favorables par le nombre d’issues total : P(événement) = nombre d'issues favorablesnombre d'issues totalnombre d'issues favorables/nombre d'issues total
Avec un dé à six faces, chaque issue a une chance sur 6 de se réaliser :
p(5) = 161/6
La probabilité d’obtenir un nombre pair est :
363/6 = 121/2 = 0,5
Avec un jeu de 52 cartes, la probabilité de tirer un roi est :
4524/52 = 1131/13 ≈ 0,08
Une urne contient deux boules vertes, cinq boules grises et une boule bordeaux, indiscernables au toucher. On tire successivement, et sans remise, deux boules.
Schématise l’arbre des probabilités.
Quelle est la probabilité de tirer une boule verte au premier tirage ?
Quelle est la probabilité de tirer une boule bordeaux au deuxième tirage ?
Correction.
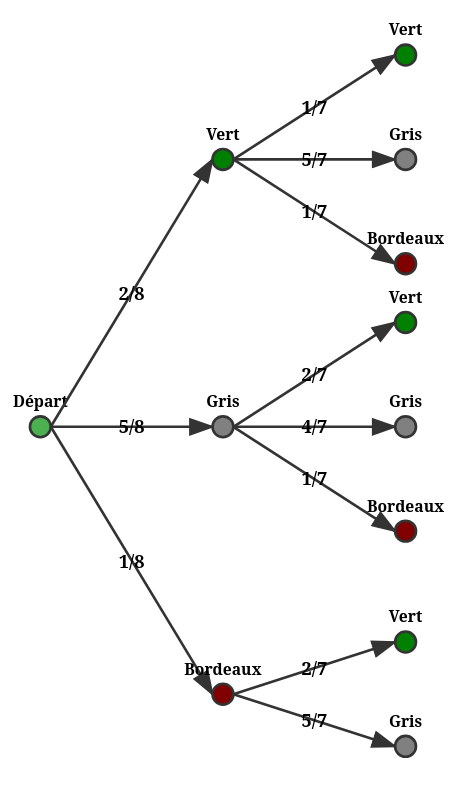
Il y a deux boules vertes sur un total de 8 boules. La probabilité de tirer une boule verte au premier tirage est :
282/8 = 141/4 = 0,25
Probabilité de tirer une boule bordeaux au deuxième tirage :
282/8 × 171/7 + 585/8 × 171/7 = 2562/56 + 5565/56
= 7567/56 = 181/8 = 0,125 = 12,5 %
Un collège propose deux activités aux élèves de 3e : canoë ou randonnée. On interroge un échantillon de 80 élèves, en distinguant filles et garçons.
| Canoë | Randonnée | Total | |
|---|---|---|---|
| Filles | 18 | 22 | ? |
| Garçons | 28 | ? | 40 |
| Total | ? | ? | 80 |
Compléter le tableau.
On choisit un élève au hasard parmi les 80. Probabilité que ce soit une fille ? qu’il ait choisi le canoë ? que ce soit un garçon ayant choisi la randonnée ?
On choisit un élève parmi ceux qui ont choisi le canoë. Probabilité que ce soit une fille ?
Correction. L’effectif total est 80 élèves, dont 40 garçons, donc 80 − 40 = 40 filles. Parmi les 40 garçons, 40 − 28 = 12 ont choisi la randonnée. Le nombre d’élèves ayant choisi le canoë est 18 + 28 = 46, la randonnée 22 + 12 = 34.
| Canoë | Randonnée | Total | |
|---|---|---|---|
| Filles | 18 | 22 | 40 |
| Garçons | 28 | 12 | 40 |
| Total | 46 | 34 | 80 |
2. a. Être une fille :
408040/80 = 121/2 = 0,5
b. Avoir choisi le canoë :
468046/80 = 234023/40 = 0,575
c. Être un garçon ayant choisi la randonnée :
128012/80 = 3203/20 = 0,15
3. Sur les 46 élèves ayant choisi le canoë, 18 sont des filles :
184618/46 = 9239/23 ≈ 0,39
Au cycle 4, un travail sur le hasard est engagé. Il vise à repérer les représentations initiales que les élèves s'en font, à les dépasser dans une perspective rationnelle pour aboutir à la notion de probabilité qui quantifie l'attente d'un événement dont la réalisation est considérée comme dépendante du hasard.
Dès le début du cycle 4, des questions relatives au hasard sont abordées à partir de situations de la vie courante (jeux, achats, médias…). La perception naturelle du hasard peut être qualifiée par des adjectifs : peu probable, probable, certain, etc.
Ces activités permettent d’introduire peu à peu les notions de probabilité, de les ordonner et de les quantifier sur une échelle de 0 à 1. L’interprétation fréquentiste permet de dépasser le modèle équiprobable dès la 4e.
Le lien entre expérience aléatoire et probabilité est construit progressivement. L’approche utilisée privilégie les expériences concrètes (tirage dans une urne, lancers de dés, etc.). Elle débouche sur l’interprétation fréquentiste, avec des comparaisons de fréquences obtenues expérimentalement. Ce lien est renforcé par le recours à des outils tels que le tableur ou la programmation.
La prise en compte des conceptions initiales des élèves sur le hasard est importante. L'effet mémoire dans les jeux de pile ou face, les idées fausses comme « il n’est pas tombé depuis longtemps » sont fréquentes. Il est donc utile de créer du conflit cognitif à partir de jeux, simulations, situations ludiques.
Le recours à l’équiprobabilité permet une première approche du calcul de probabilité par dénombrement. Mais il est important de ne pas s’y limiter. L’étude de cas non équiprobables (urnes déséquilibrées, biais, etc.) permet d’approfondir la notion.
Les probabilités permettent également de travailler les grandeurs (longueur, aire, volume) dans le cadre de tirages aléatoires sur des supports géométriques.
Les activités autour des statistiques et probabilités permettent de mobiliser :
Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.
Le manuel : 7,50 €
Voir aussi : toutes les leçons · tous les exercices corrigés · toutes les questions flash · toutes les fiches de révision · annales du brevet
Cette page est développée en php avec l'éditeur de texte du projet GNOME. Elle se veut conforme aux instructions officielles de l'Éducation nationale.
Référence au programme : Programme de mathématiques du cycle 4 (arrêté du 9 novembre 2015 modifié), encore en vigueur en classe de troisième ; le nouveau programme (arrêté du 18 février 2026) s'y appliquera à la rentrée 2028. Domaine : Organisation et gestion de données.
lecon.body.tex : même texte et même plan que le PDF, la source LaTeX et le module TBI.N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
☕ Payez-moi un café via PayPal
Partager :
🔑 Accéder à une fiche par son code
Demande le code à ton professeur.
Exemples : PYTH0123, PMDE161842, SOMP0042.