Les éléments de géométrie en sixième

I. Le point

Introduction (orale)

En géométrie on parle souvent de points. Dans les éléments d'Euclide livre 1, la définition du point est la suivante : « Le point est ce qui n'a aucune partie. » Il n'a ni longueur, ni largeur ni épaisseur.

On peut imaginer simplement le point comme un "endroit", un lieu. Et dans cet endroit, dans ce lieu, il n'y a ... RIEN.

Il est si "petit" qu' on ne peut donc pas le représenter facilement !

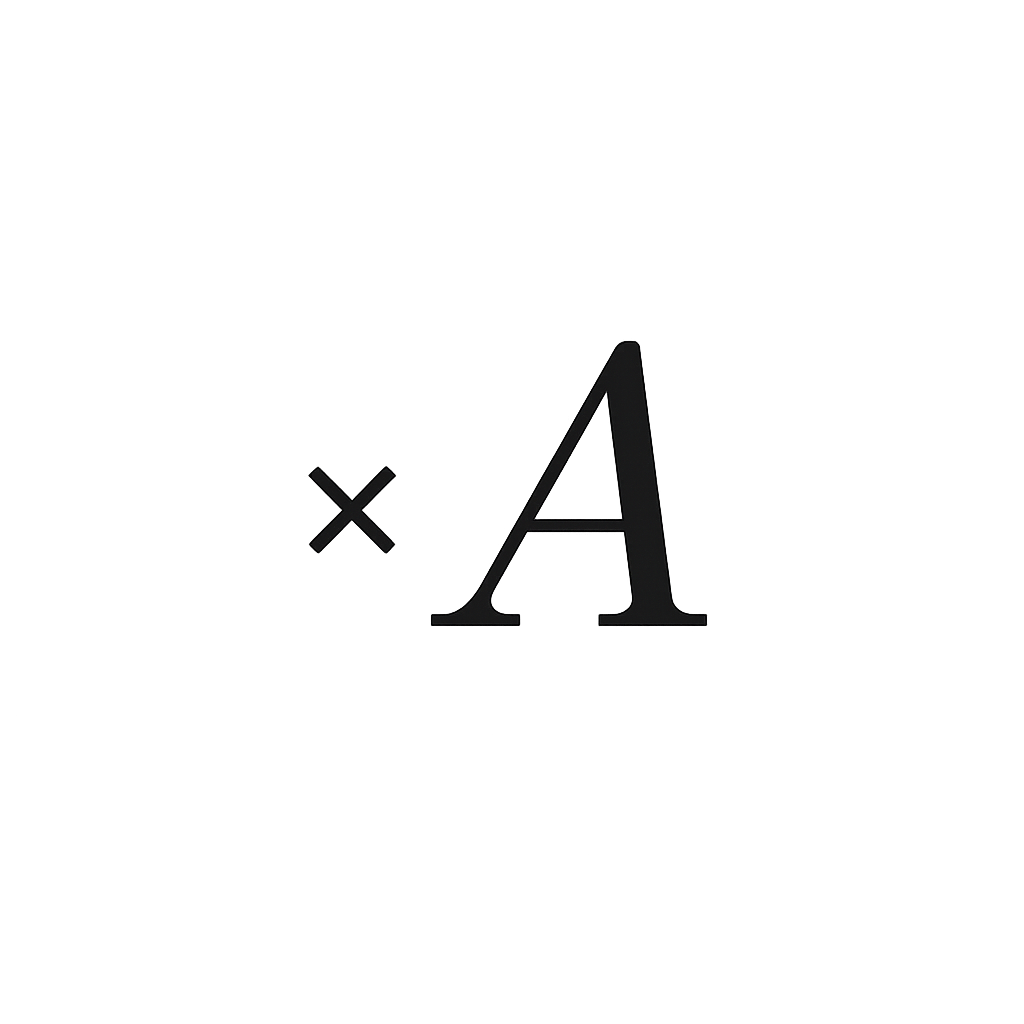
Le point A est symbolisé par la petite croix

Attention de ne pas confondre le nom du point avec le point lui même !

II. Le segment [AB]

A. Définition

Le segment [AB] est constitué de tous les points alignés avec A et B, entre A et B. On le note avec des crochets. Les points A et B sont les extrémités du segment [AB].

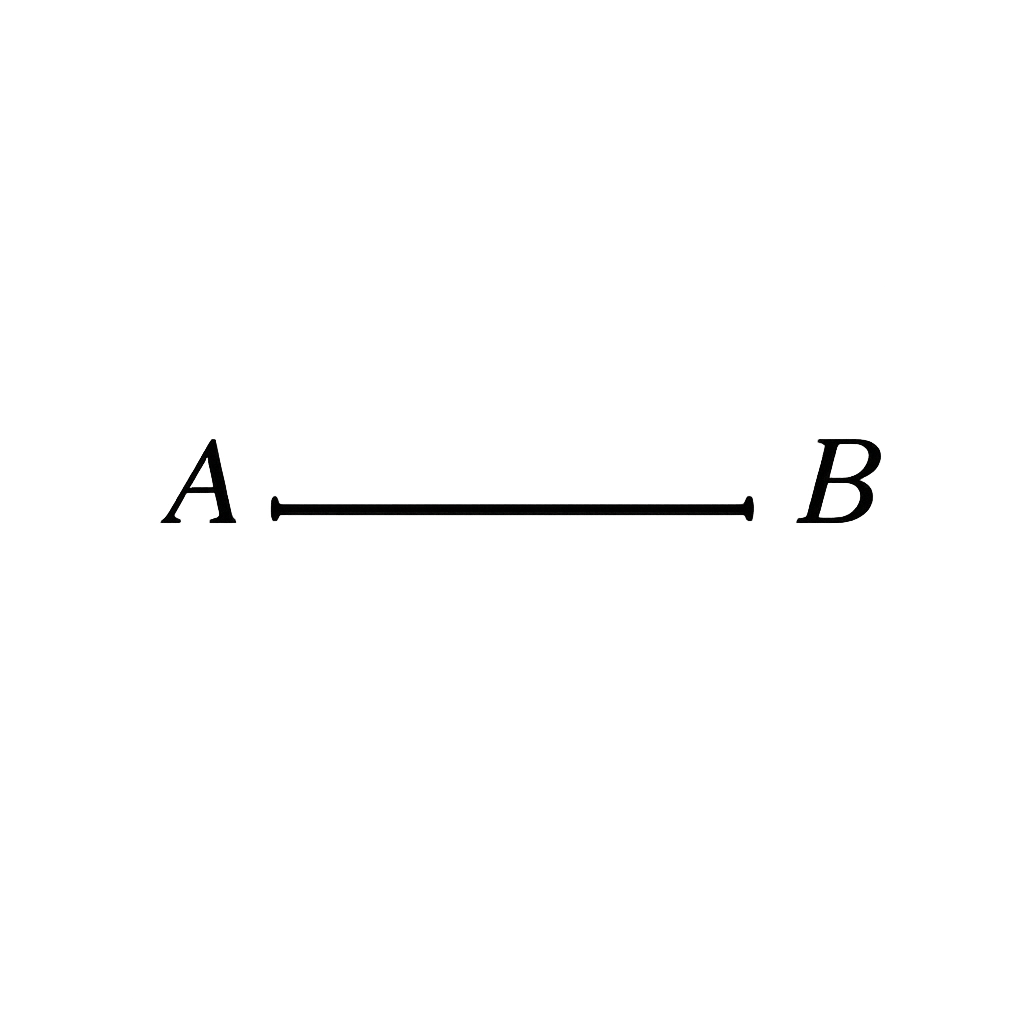
Si le segment [AB] mesure 5cm, on note AB=5cm, cette fois ci sans crochet.

• [AB] désigne donc l'objet segment
• AB est un nombre (avec une unité), c'est la longueur du segment [AB]

B. Propriété

Si deux segments [AB] et [CD] ont la même longueur on dit qu'ils sont égaux, on note AB=CD et on code comme sur le dessin ci-dessous :

III La demi-droite

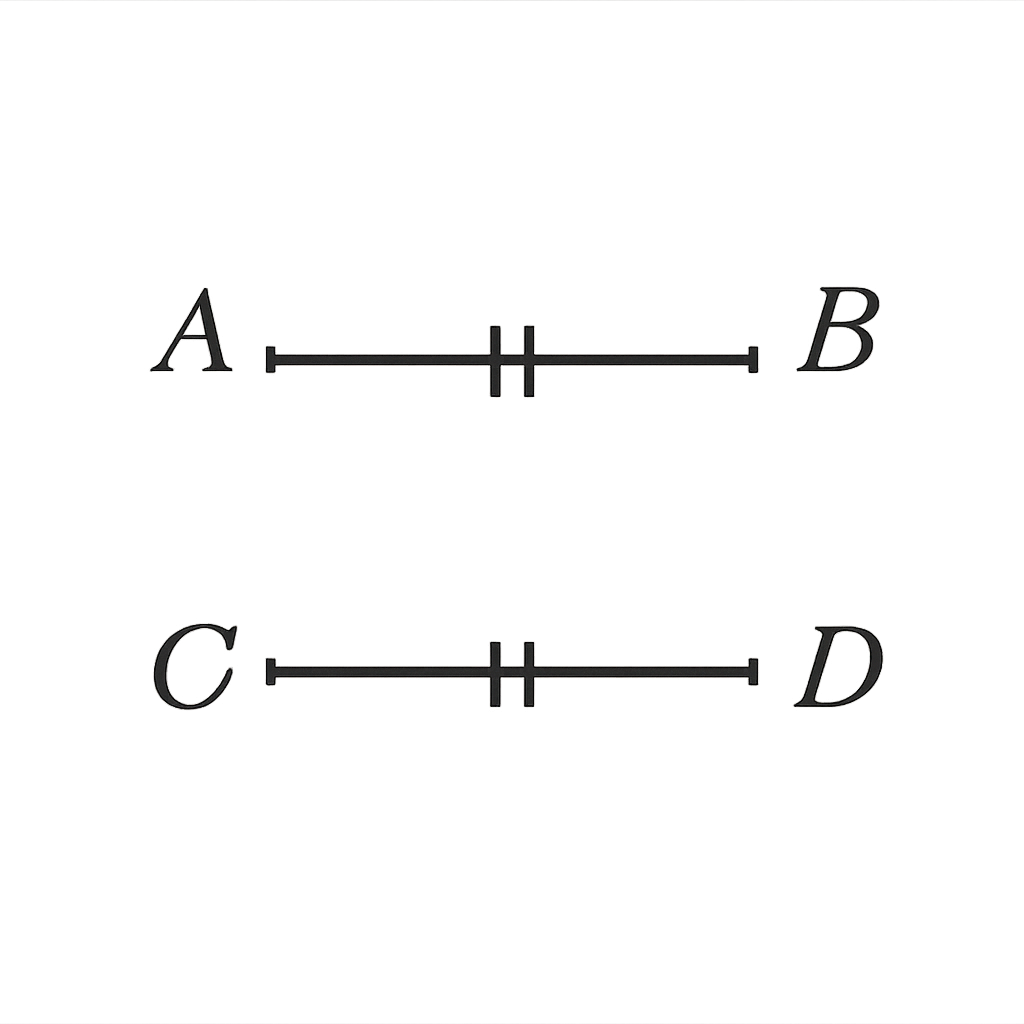
Si on prolonge le segment [AB] indéfiniment (sans jamais s'arrêter) du côté de B (seulement) on obtient un nouvel objet mathématique : La demi-droite [AB). On dit aussi la demi-droite d'origine A, passant par B.

Remarque 1:

Quand on représente une demi-droite on s'arrête (un jour) de prolonger le segment mais la demi-droite continue, continue, continue !

Remarque 2:

On nomme parfois une demi-doite avec une lettre majuscule qui désigne l'origine de la demi-droite et une lettre minuscule qui désigne la branche infinie de cette demi-droite (et non pas un point). Exemple : le demi-droite [Px).

IV Droite

Si on prolonge le segment [AB] indéfiniment (sans jamais s'arrêter) des deux côtés on obtient un nouvel objet mathématique : La droite (AB)

Remarque:

Sur le dessin ci-dessus on a représenté la droite (AB) mais les objets segments [AB], demi-droite [AB), demi-droite [BA) existent aussi !

V Appartenance

Soit un segment [AB] et un point M appartenant au segment [AB]

On note M ∈ [AB] et on lit : Le point M appartient au segment [AB]

A votre avis, comment écrit-on mathématiquement que le point N n'appartient pas au segment [CD] ?

VI Milieu

Définition

On appelle milieu d'un segment le point d'un segment à la même distance de ses extrémités.

Remarques

Il y a deux informations dans la définition :

Si M est le milieu du segment [AB]:

• M ∈[AB] (M appartient au segment)
• MA=MB (M est équidistant de A et B)

Codage :

On n'oublie pas de coder l'égalité des segments [MA] et [MB] !