Ce site utilise Google Analytics, Google AdSense et le service de chat Crisp pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Les mathématiciens manipulent parfois de grands nombres, mais jamais dans leurs revenus.
🔑 Code de cette page :
Une expérience aléatoire est une expérience dont on ne peut pas prévoir le résultat à l'avance, mais dont on connaît tous les résultats possibles.
Exemples :
• Lancer un dé à 6 faces
• Lancer une pièce de monnaie
• Tirer une boule dans un sac sans regarder
• Faire tourner une roue de la fortune
Un dé et une pièce : deux objets classiques pour les expériences aléatoires
Une issue est un résultat possible d'une expérience aléatoire.
Exemple : Pour un lancer de dé à 6 faces, les issues possibles sont : 1, 2, 3, 4, 5 et 6.
Un événement est un ensemble d'une ou plusieurs issues.
Exemples d'événements pour un lancer de dé :
• "Obtenir un nombre pair" : les issues sont 2, 4 et 6
• "Obtenir un nombre supérieur à 4" : les issues sont 5 et 6
• "Obtenir le nombre 3" : une seule issue, le 3
La probabilité d'un événement est un nombre qui mesure les chances que cet événement se réalise. Ce nombre est toujours compris entre 0 et 1.
• Une probabilité de 0 signifie que l'événement est impossible
• Une probabilité de 1 signifie que l'événement est certain
• Plus la probabilité est proche de 1, plus l'événement a de chances de se réaliser
Exemple 1 : Lancer de dé
Quelle est la probabilité d'obtenir un nombre pair avec un dé à 6 faces ?
Issues favorables : 2, 4, 6 (3 issues)
Issues possibles : 1, 2, 3, 4, 5, 6 (6 issues)
Probabilité : 363/6 = 121/2
Exemple 2 : Tirage de boules
Un sac contient 4 boules rouges, 3 boules bleues et 2 boules vertes. On tire une boule au hasard. Quelle est la probabilité de tirer une boule rouge ?
Nombre de boules rouges : 4
Nombre total de boules : 4 + 3 + 2 = 9
Probabilité : 494/9
Une probabilité peut s'écrire de plusieurs façons :
| Fraction | Décimal | Pourcentage | Expression |
|---|---|---|---|
| 121/2 | 0,5 | 50 % | "Une chance sur deux" |
| 141/4 | 0,25 | 25 % | "Une chance sur quatre" |
| 343/4 | 0,75 | 75 % | "Trois chances sur quatre" |
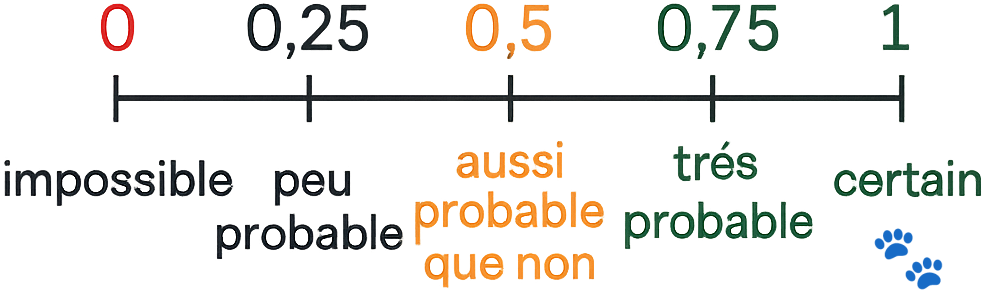
L'échelle des probabilités va de 0 (impossible) à 1 (certain)
Sur cette échelle :
• 0 correspond à un événement impossible
• 121/2 correspond à un événement qui a autant de chances de se produire que de ne pas se produire
• 1 correspond à un événement certain
À retenir : La probabilité est toujours un nombre entre 0 et 1 !
Une roue divisée en secteurs égaux
Exercice témoin : Une roue est divisée en 9 secteurs égaux : 4 rouges, 3 bleus, 1 vert et 1 jaune. On fait tourner la roue une fois.
Solutions :
Exemple : Dans un jeu de 32 cartes, quelle est la probabilité de tirer un as ?
Il y a 4 as dans un jeu de 32 cartes
Probabilité = 4324/32 = 181/8
• Un événement impossible a une probabilité de 0
• Un événement certain a une probabilité de 1
Exemples avec un dé à 6 faces :
• "Obtenir 7" : probabilité = 060/6 = 0 (impossible)
• "Obtenir un nombre entre 1 et 6" : probabilité = 666/6 = 1 (certain)
Quand on répète une expérience aléatoire un grand nombre de fois, la fréquence d'apparition d'un événement se rapproche de sa probabilité.
Exemple : Si on lance une pièce 1000 fois, on obtiendra environ 500 fois "pile" et 500 fois "face", car la probabilité de chaque face est 121/2.
Pour certaines expériences, on peut représenter toutes les issues possibles dans un arbre :
L'arbre permet de visualiser toutes les issues possibles et facilite le calcul des probabilités.
Références : Arrêté du 10 avril 2025 fixant les programmes du cycle de consolidation (cycle 3) — BO du 16/04/2025, et page éduscol « Mathématiques – cycle 3 » annonçant l’entrée progressive en vigueur (6e à la rentrée 2025-2026).
Sources officielles : BO — Arrêté du 10/04/2025 (cycle 3) · Annexes Mathématiques (PDF) · Éduscol — Mathématiques cycle 3
Partager :
🔑 Accéder à une fiche par son code
Demande le code à ton professeur.
Exemples : PYTH0123, PMDE161842, SOMP0042.