Ce que femme veut Dieu le veut.
Une fraction est une écriture de la forme a b où a est le numérateur et b est le dénominateur (avec b ≠ 0).
Sur un ordinateur, on écrit souvent une fraction sous la forme a/b (c'est plus pratique avec un clavier !).
Mais dans un cahier, on préfère une écriture verticale.
Une expression comme a b est une fraction si a et b sont des entiers.
Tout nombre entier peut s'écrire sous forme de fraction. Par exemple : 4 = 41
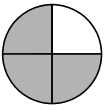
Le disque est partagé en 4 parts égales, et 3 parts sont coloriées : 3 4 du disque sont coloriées.
Sauf exceptions (demi, tiers, quart), on lit le numérateur puis le dénominateur avec le suffixe ième.
Une fraction ab est le nombre qui, multiplié par b, donne a.
Par exemple, 35 est le nombre qui, multiplié par 5, donne 3.
Est-ce que la fraction est inférieure, égale ou supérieure à 1 ? C’est la grande question !
Toute fraction peut s’écrire comme la somme d’un entier et d’une fraction inférieure à 1.
Écrivons 85 sous forme d'une somme d’un entier et d'une fraction :
On partage une figure en 5 parts égales (cinquièmes), puis on colorie 8 parts :
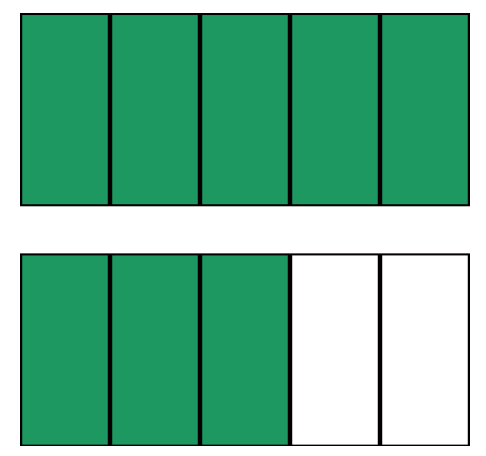
On obtient : 85 = 1 + 35
35
est inférieure à 1.
85
est comprise entre 1 et 2 :
1 <
85
< 2
Place le point A d’abscisse 56 sur une demi-droite graduée.
On choisit une unité, on la partage en 6 parts égales, puis on avance de 5 parts depuis O.
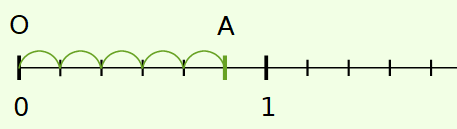
Au cycle 3, l'étude des grands nombres permet d'enrichir la compréhension de notre système de numération (numération orale et numération écrite) et de mobiliser ses propriétés lors de calculs.
Les fractions puis les nombres décimaux apparaissent comme de nouveaux nombres introduits pour pallier l'insuffisance des nombres entiers, notamment pour mesurer des longueurs, des aires et repérer des points sur une demi-droite graduée.
Le lien à établir avec les connaissances acquises à propos des entiers est essentiel. Avoir une bonne compréhension des relations entre les différentes unités de numération des entiers (unités, dizaines, centaines de chaque ordre) permet de les prolonger aux dixièmes, centièmes...
Les caractéristiques communes entre le système de numération et le système métrique sont mises en évidence.
L'écriture à virgule est présentée comme une convention d'écriture d'une fraction décimale ou d'une somme de fractions décimales. Cela permet de mettre à jour la nature des nombres décimaux et de justifier les règles de comparaison (qui se différencient de celles mises en oeuvre pour les entiers) et de calcul.
Résoudre des problèmes en utilisant des fractions simples,les nombres décimaux et le calcul
Composer, décomposer les grands nombres entiers, en utilisant des regroupements par milliers.
Unités de numération (unités simples, dizaines, centaines,milliers, millions, milliards) et leurs relations.
Comprendre et appliquer les règles de la numération aux grands nombres (jusqu'à 12 chiffres). Comparer, ranger, encadrer des grands nombres entiers, les repérer et les placer sur une demi-droite graduée adaptée.
Comprendre et utiliser la notion de fractions simples.
Repérer et placer des fractions sur une demi-droite graduée adaptée.(Une première extension de la relation d'ordre.)
Encadrer une fraction par deux nombres entiers consécutifs.
Établir des égalités entre des fractions simples.
Partager: