Ce site utilise Google Analytics, Google AdSense et le service de chat Tawk.to pour mesurer l'audience, afficher des annonces et proposer une assistance en ligne. Acceptez-vous le dépôt de cookies ?
Il vaut mieux qu'il pleuve aujourd'hui qu'un jour où il fait beau !
Pierre Dac (sur mon T shirt!)
Chaque jour sur cette page, découvrez un nouveau problème (corrigé) du type "Trouvez le plus long chemin !"
Les problèmes de cette page s'adresse à tout le monde. Bien sûr, les méthodes de résolution sont elles fonctions du niveau d'étude. Amusez-vous sans modération avec ces problèmes, nouveaux chaque jour!
La correction est plus bas dans la page !
Aux échecs le déplacement du cavalier est original. Il se déplace en L
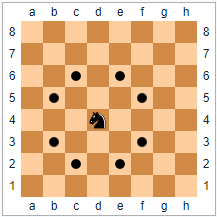
Sur l'échiquier ci-dessous, on imagine un cavalier sur une case, (celle de votre choix) puis on le déplace vers une autre case contenant un nombre supérieur, et on recommence tant que c'est possible...
| 4 | 13 | 8 | 11 | 14 | 15 |
| 3 | 1 | 3 | 12 | 9 | 4 |
| 2 | 7 | 6 | 18 | 20 | 17 |
| 1 | 10 | 2 | 5 | 19 | 16 |
| A | B | C | D | E |
Quel est le plus long chemin ?
| 4 | 13 | 8 | 11 | 14 | 15 |
| 3 | 1 | 3 | 12 | 9 | 4 |
| 2 | 7 | 6 | 18 | 20 | 17 |
| 1 | 10 | 2 | 5 | 19 | 16 |
| A | B | C | D | E |
Pour accéder à nos ressources gratuites, il vous suffit de sélectionner l'activité que vous désirez dans le formulaire au dessus de l'activité du jour. Ensuite, utilisez l'icône appropriée sous les liens de partage pour télécharger vos PDF.
N'oubliez pas, partager fait vivre les sites ! 😊 Merci de votre soutien !
J'ai réalisé cette activité en Python3. Mon travail est sous licence Creative commons et mon code est disponible sur simple demande .
N'hésitez pas à me contacter si vous detectez la moindre imperfection, ou si vous imaginez une amélioration potentielle !
Open source et gratuité n’empêchent ni les dons ni les remerciements 😉
Un euro ou deux pour m’aider à payer le serveur ?
💙 Faire un don sur PayPal
Partager: