Arithmétique

I. RAPPELS : LES ENSEMBLES DE NOMBRES

1) Les entiers naturels :

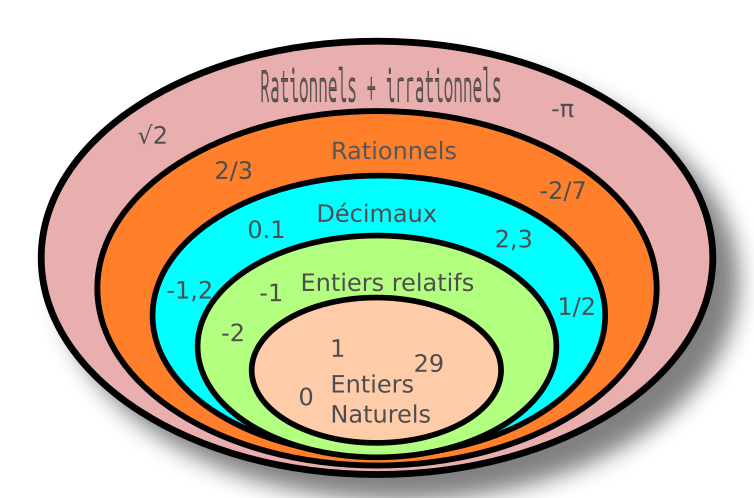
Ce sont les nombres que l'on peut compter sur ses doigts.

ex : 0 ; 1 ; 2 ...

2) Les entiers relatifs :

Ce sont les entiers naturels et leurs opposés.

ex : ... ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ...

3) Les nombres rationnels :

Ce sont les résultats des divisions de 2 nombres entiers relatifs.

Si la division tombe juste, on les appelle aussi " décimaux ".

ex : = 0,5

Certains rationnels sont négatifs.

ex :-2/3 = -0,66666...

4) Les nombres irrationnels :

π ; √2

II. Exercices témoins, classiques avec les entiers naturels

A. Encadrer un entier par deux multiples consécutifs

Encadre 413 par deux multiples consécutifs de 21

Réponse : On effectue la division euclidienne de 413 par 21 :

413 = 21 × 19 + 14
413 = 399 + 14
Donc 399 ≤ 413 < 420

On a bien "coincé" 413 entre deux multiples de 21 :

• 21 × 19 = 399 et
• 399 + 21 = 420 = 21 × 20

B. Trouver le plus grand multiple d'un nombre inférieur à un nombre donné

Quel est le plus grand multiple de 27 inférieur à 112 ?

Division euclidienne : 112 = 27 × 4 + 4 et 4 < 27
Donc le plus grand multiple de 27 inférieur à 112 est
27 × 4 = 108 = 112 - 4

C. Trouver le plus petit multiple d'un nombre supérieur à un nombre donné

Quel est le plus petit multiple de 8 supérieur à 387 ?

Division euclidienne : 387 = 8 × 48 + 3 et 3 < 8
Donc le plus petit multiple de 8 supérieur à 387 est
8 × (48 + 1) = 8 × 49 = 392

III. NOMBRES PREMIERS

A. Comprendre la notion de "nombre premier"

On appelle nombre premier un entier naturel qui possède exactement deux diviseurs distincts : 1 et lui-même.

B. les premiers nombres premiers

C. Décomposer un nombre en facteurs premiers

Décompose 1350 en facteurs premiers.

On divise successivement 1350 par des facteurs premiers "qui vont bien" (En se servant de la liste ci-dessus et éventuellement des critères de divisibilités)

Décomposition en facteurs premiers :

1350	2
675	3
225	3
75	3
25	5
5	5

1350 =
2 × 3 × 3 × 3 × 5 × 5 =
2 × 3³ × 5²

IV. PLUS GRAND COMMUN DIVISEUR DE DEUX NOMBRES :

A. Définition 1

a et k étant deux entiers naturels avec k différent de 0. Lorsque a/k est un entier naturel, on dit que k est un diviseur de a. (c'est à dire quand le reste de la division euclidienne de a par k est zéro)

(On dit aussi que a est un multiple de k, ou encore que a est divisible par k)

Exemples : 18 = 2 x 9
2 est un diviseur de 18 et 9 est un autre diviseur de 18.

B. Lister les diviseurs d'un entier naturel

Donne la liste des diviseurs de 260

On peut commencer par décomposer 260 en facteurs premiers, comme dans l'exercice témoin précédent :
260 = 2 × 2 × 5 × 13
Les diviseurs de 260 sont donc :

• 1
• 2
• 2 × 2 = 4
• 5
• 2 × 5 = 10
• 13
• 2 × 2 × 5 = 20
• 2 × 13 = 26
• 2 × 2 × 13 = 52
• 5 × 13 = 65
• 2 × 5 × 13 = 130
• 2 × 2 × 5 × 13 = 260

Et on écrit (en notation ensembliste):
260 : {1 ; 2 ; 4 ; 5 ; 10 ; 13 ; 20 ; 26 ; 52 ; 65 ; 130 ; 260}

C. Définition 2

Si deux entiers naturels a et b sont divisibles par un même entier naturel k, on dit que k est un diviseur commun de a et b.

Exemple :
36=12x3 et 24=12x2, donc 12 est un diviseur de 36 et 24.
36=8x4,5 et 24=8x3, donc 8 n'est pas un diviseur commun de 36 et 24 car il ne divise pas 36.

Remarque : 1 est un diviseur commun à tous les nombres.

Donne la liste des diviseurs communs à 435 et 135

Liste des diviseurs:
435 : {1 ; 3 ; 5 ; 15 ; 29 ; 87 ; 145 ; 435}
135 : {1 ; 3 ; 5 ; 9 ; 15 ; 27 ; 45 ; 135}
La liste des diviseurs commun à 435 et 135 est:
{1 ; 3 ; 5 ; 15}

D. Notation

si a et b désignent deux nombres entiers relatifs, on note PGCD(a ; b) le plus grand des diviseurs positifs communs à a et b.

Quel est le plus grand diviseur commun de 24 et 36?

La liste des diviseurs de 24 est :
{ 1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12; 24}

La liste des diviseurs de 36 est :
{1 ; 2 ; 3 ; 4 ; 6 ; 9 ;12 ; 18 ; 36}

24 et 36 ont 6 diviseurs communs :
{1 ; 2 ; 3 ; 4 ; 6 ; 12}

Le plus grand d'entre eux est 12, c'est le plus grand diviseur commun de 24 et 36.
On note PGCD(24 ; 36) = PGCD(36 ;24) = 12

V. ALGORITHMES DE RECHERCHE DU PGCD :

A. Algorithme des différences :

Pour déterminer PGCD(295 ; 177), on effectue les soustractions successives :

• 295-177=118
• 177-118=59
• 118-59=59

• On prend les deux nombres et on les soustrait.
• On prend les deux plus petits et on recommence.
• On s'arrête lorsque l'on obtient deux nombres égaux.

Propriété :

Le plus grand diviseur commun est le dernier reste non nul dans la succession des différences de l'algorithme.

Quel est le PGCD de 150 et 40? (algorithme des soustractions successives)

Calcul du PGCD de 150 et 40 par soustractions successives :
150 − 40 = 110
110 − 40 = 70
70 − 40 = 30
40 − 30 = 10
30 − 10 = 20
20 − 10 = 10
PGCD( 150 ; 40 ) = 10

B. l'algorithme d'Euclide.

Pour déterminer PGCD(252 ; 360) :

• Effectuer la division euclidienne du plus grand des deux nombres par le plus petit :
  360 = 252 x 1 + 108
• Effectuer la division euclidienne du diviseur par le reste de la division précédente, jusqu'à ce que le reste de la division soit égal à 0.
• 252 = 108 x 2 + 36
• 108 = 36 x 3 + 0

Le plus grand diviseur commun est le dernier reste non nul dans la succession des divisions euclidiennes de l'algorithme d'Euclide.(ici 36)

Déterminez le PGCD de 48 et 70 par l'algorithme d'Euclide.

Algorithme d’Euclide :
48 = 70 × 0 + 48
70 = 48 × 1 + 22
48 = 22 × 2 + 4
22 = 4 × 5 + 2
4 = 2 × 2 + 0
PGCD ( 48 ; 70 ) = 2

VI. Plus Petit Commun Multiple (PPCM) :

A. Définition

Le PPCM de deux nombres est le plus petit entier naturel qui est un multiple commun à ces deux nombres.

Le PPCM est souvent utilisé pour trouver un dénominateur commun quand on additionne ou soustrait des fractions.

B. Exemple

Exemple :
Les multiples de 4 sont : 4, 8, 12, 16, 20, 24, 28, 32, ...
Les multiples de 6 sont : 6, 12, 18, 24, 30, 36, ...
Les multiples communs sont : 12, 24, 36, ...
Le plus petit d'entre eux est 12 : on dit que PPCM(4 ; 6) = 12

C. En utilisant la décomposition

4 = 2²
6 = 2 × 3
Un multiple de 4 et 6 devra (au minimum) être multiple de 2² × 3 = 4 × 3 = 12
PPCM(4 ; 6) = 12

D. Exercice témoin, type Brevet

Deux ampoules clignotent.
L’une s’allume toutes les 9 min et 48 s et l’autre toutes les 5 min et 48 s .
À minuit, elles s’allument ensemble.

Détermine l’heure à laquelle elles s’allumeront de nouveau ensemble.

Temps en secondes:

Ampoule 1 : 9 × 60 + 48 = 588
Ampoule 2 : 5 × 60 + 48 = 348

Décomposition en facteurs premiers:

588 = 2² × 3 × 7²
348 = 2² × 3 × 29

Plus petit multiple commun:

2² × 3 × 7² × 29 = 17052

Conversion et conclusion

17052 = 284 × 60 + 12
284 = 4 × 60 + 44
→ 4 h 44 min 12 s.

les ampoules s’allumeront de nouveau ensemble à 4 heures 44 minutes et 12 secondes.

VII. NOMBRES PREMIERS ENTRE EUX. FRACTIONS IRREDUCTIBLES :

A. Nombres premiers entre eux :

On dit que deux nombres a et b sont premiers entre eux lorsque leur plus grand diviseur commun est égal à 1.

Exemples :

1) 10 et 7 sont premiers entre eux ; en effet :
les diviseurs de 10 sont { 1 ; 2 ; 5 ; 10 }
les diviseurs de 7 sont { 1 ; 7 }
donc PGCD(10 ; 7) = 1 et 10 et 7 sont premiers entre eux.

2) 221 et 69 sont premiers entre eux ; en effet, en appliquant l'algorithme d'Euclide,

• 221 = 69 x 3 + 14
• 69 = 14 x 4 + 13
• 14 = 13 x 1 + 1
• 13 = 1 x 13 + 0

donc PGCD(221 ; 69) = 1.

B. Fraction irréductible :

On dit qu'une fraction est irréductible lorsque son numérateur et son dénominateur sont premiers entre eux.

Exemples : PGCD(10 ; 7) = 1 donc 10 7 est une fraction irréductible.

C.Propriété :

Lorsque l'on simplifie une fraction par le plus grand diviseur commun à son numérateur et son dénominateur, la fraction obtenue est irréductible.

Exemples :
On sait que PGCD(252 ; 360) = 36 donc :

252 360 = 252 : 36 360 : 36 = 7 10 est une fraction irréductible.

Le Cahier d'exercices iParcours Maths 3e avec cours (édition 2022) est un cahier-manuel de160 pages, avec un cours complet en début de chaque chapitre et de nombreux exercices associés, notamment pour la préparation au Brevet.

Le manuel : 7,50 €

Plus de Produits