Les conseils de Wouf

Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.

Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.

Il faut améliorer la condition féminine : par exemple agrandir les cuisines, baisser les éviers ou mieux isoler les manches des casseroles.

Georges Wolinski (sur mon T shirt!)

Voir toutes les citations.

Magic 500

Magic 500 n'est que le jeu où l'on devine un nombre, après essais successifs (trop grand, trop petit...)

Développé par les membres de Microloges, le club d'informatique de Beaumetz les loges, Magic 500 présente l'interêt d'offrir des sources quickbasic qui peuvent servir d'exemples aux débutants...

source: magic.bas

Le fichier principal:

DECLARE SUB jeu (moinsbon!)
DECLARE SUB regle ()
DECLARE SUB beethov ()
DECLARE SUB init (e$)
DECLARE SUB texte (a$, li!, co!, couleur!, t$)
DECLARE SUB espace (w!)
DECLARE SUB elise ()
CONST nbnb = 5         'nb de nb à trouver
CONST nbch = 3          'nb de chiffre à trouver
CONST nbenr = 30
TYPE sov
      chnom AS STRING * 20
      chnbes AS INTEGER
     END TYPE

DIM joueur AS sov
joueur.chnom = "Adam"


'                              Page de garde...
'__________________________________________________

DO


WIDTH 40, 25
CLS

texte "MICRoLoGES", 12, 5, 3, "non"

elise

texte "PRESENTE:", 14, 10, 4, "oui"

CLS

texte " M A G I C  5 0 0", 12, 1, 5, "non"

SLEEP 2
'_______________________________________________
'page 2

WIDTH 80, 50
CLS
OPEN "score.wou" FOR RANDOM AS #1 LEN = LEN(joueur)
i = 1

texte "MEILLEURS SCORES", 1, 25, 2, "non"
texte "NOM", 5, 15, 3, "non"
texte "ESSAIS", 5, 50, 3, "non"

max = LOF(1) / LEN(joueur)

IF max > nbenr THEN max = nbenr

FOR i = 1 TO max
  GET #1, i, joueur




  LOCATE 7 + i, 2
  COLOR 1
  PRINT i
  LOCATE 7 + i, 15
  PRINT joueur.chnom
  LOCATE 7 + i, 50
  COLOR 5
  PRINT joueur.chnbes


 NEXT



CLOSE #1
moinsbon = joueur.chnbes
IF moinsbon = 0 OR max < nbenr THEN moinsbon = 9999


LOCATE 50, 35
COLOR 2
PRINT "J";
COLOR 1
PRINT "ouer/";
COLOR 2
PRINT "R";
COLOR 1
PRINT "ègles/";
COLOR 2
PRINT "Q";
COLOR 1
PRINT "uitter";





DO
init e$  'on initialise la liste de nb aleatoires
LOOP UNTIL INSTR("jJrRqQ", e$) > 0 AND e$ <> ""



 


 SELECT CASE UCASE$(e$)


 CASE "J"
	jeu moinsbon

 CASE "Q"
 fin$ = "oui"

 CASE "R"
       regle

 END SELECT

 LOOP UNTIL fin$ = "oui"

SUB jeu (moinsbon)
DIM joueur AS sov
    DIM j AS sov
CLS
WIDTH 80, 50
BEEP

FOR no = 1 TO nbnb

 nbcach = INT(RND * 9 * 10 ^ (nbch - 1)) + 10 ^ (nbch - 1)
 DO
   essai = essai + 1
   PRINT
   COLOR 3
   PRINT "Encore "; nbnb - no + 1; "nombre";
   IF nbnb - no + 1 > 1 THEN PRINT ("s");
   PRINT " ...trouver. ";

  
   COLOR 3
   PRINT " Essai nø ";
   COLOR 4
   PRINT essai;
   COLOR 3
   PRINT " >  ";
   t = 0


   FOR y = 1 TO nbch

   t$ = ""
     DO
      t$ = INKEY$
     LOOP UNTIL INSTR("0123456789q", t$) > 0 AND t$ <> ""
     IF t$ = "q" THEN STOP
   PRINT t$;
   t = t * 10 + VAL(t$)

   t$ = ""
   
   
   NEXT y
  
   IF t > nbcach THEN PRINT "   trop grand "
   IF t < nbcach THEN PRINT "   trop petit "


 LOOP UNTIL t = nbcach
   COLOR 4
   PRINT " BRAVO !"
   IF no <nbnb THEN elise ELSE beethov
   espace (5)


NEXT no


PRINT "                           Mission accomplie !"
SLEEP 3

' ici on regarde le score et on le sauve si il est bon

IF essai < moinsbon THEN
PRINT " Bravo ! Vous entrez dans le top "; nbenr
PRINT
BEEP

INPUT "Entrez votre nom : "; nom$
OPEN "score.new" FOR RANDOM AS #2 LEN = LEN(joueur)

OPEN "score.wouf" FOR RANDOM AS #1 LEN = LEN(joueur)

 ok$ = "non"
 
 i2 = 0
 
 
max = LOF(1) / LEN(joueur)
 IF max = 0 THEN
       ok$ = "oui"
       j.chnom = nom$
       j.chnbes = essai
       i2 = i2 + 1
       PUT #2, i2, j
     END IF


 FOR i = 1 TO max

 GET #1, i, joueur

  IF (essai < joueur.chnbes OR joueur.chnbes = 0) AND ok$ = "non" THEN
       ok$ = "oui"
      
       j.chnom = nom$
       j.chnbes = essai
       i2 = i2 + 1
       PUT #2, i2, j
      
      
       END IF

       i2 = i2 + 1
       PUT #2, i2, joueur
      

 NEXT

 IF ok$ = "non" THEN

       ok$ = "oui"
     
       j.chnom = nom$
       j.chnbes = essai
       i2 = i2 + 1
       PUT #2, i2, j
      END IF


CLOSE #2
CLOSE #1

KILL "score.wou"
NAME "score.new" AS "score.wou"


END IF


END SUB

SUB regle
WIDTH 40, 25

CLS
texte "Règles", 5, 10, 5, "non"
texte "du jeu", 5, 23, 5, "oui"
espace (5)
COLOR 4
PRINT "Il s'agit de découvrir ";
PRINT nbnb;
PRINT " nombres cachés en dépensant"
PRINT "le moins d'essais possibles."
PRINT
PRINT " Les nombres sont des entiers de "; nbch; " chiffres"
PRINT
PRINT " plus petit, ou plus grand"
PRINT "seront mes seules indications"
PRINT
texte "BONNE CHANCE", 23, 12, 3, "oui"

LOCATE 25, 10
COLOR 4
PRINT " presser une touche";
SLEEP

END SUB

source: divers.bas

Et ce fichier externe, comme un "include"...

SUB beethov
ECOUTE$ = "T180 o2 P2 P8 L8 GGG L2 E-"
SUITE$ = "P24 P8 L8 FFF L2 D"
PLAY ECOUTE$ + SUITE$

END SUB

SUB elise
   PLAY ON
   lise$ = "o3 L8 E D+ E D+ E o2 B o3 D C L2 o2 A"
   PLAY "MB X" + VARPTR$(lise$)

END SUB

SUB espace (w)
FOR i = 1 TO w
 PRINT
 NEXT

END SUB

SUB init (e$)
DO
e$ = INKEY$
z = z + 1
LOOP UNTIL e$ <> ""
RANDOMIZE (z)

END SUB

SUB texte (a$, li, co, couleur, t$)
      
      LOCATE li, co
      COLOR couleur
      FOR i = 1 TO LEN(a$)
       PRINT (MID$(a$, i, 1)); " ";
       IF t$ = "oui" THEN SLEEP 1
       NEXT



END SUB

Téléchargements:

Télécharger le zip (EXE + sources)

Liens divers:

Quick Basic

Quick Basic est téléchargeable: qb45fr.zip

Un autre exemple sur Wikipedia: Exemple de programme sous Qbasic

Tweets by wouf

Comment ???

NEWS

Page : https://site2wouf.fr/magic500.php
Catégorie : Informatique

Des Mathématiques combinatoires avec Python et itertools.combinations

En Mathématiques, “choisir” sans tenir compte de l’ordre, c’est la combinaison. En Python, c’est exactement ce que fait itertools.combinations : il énumère toutes les sélections possibles de taille k parmi une liste, sans doublon, et sans permutation inutile. Résultat : du code plus clair, plus sûr… et souvent plus rapide que des boucles bricolées.

Une combinaison de taille p parmi n objets, c’est un choix sans ordre.

{A, B, C} et {C, B, A} représentent la même combinaison.
Le nombre de choix possibles est le coefficient binomial : [katex]C_n^p[/katex]

[katex]C_n^p[/katex], souvent écrit [katex]\binom{n}{p}[/katex] dans la littérature anglo-saxonne et en informatique.

[katex]C_n^p[/katex] se lit : « p parmi n »

Cela désigne le nombre de combinaisons de p éléments choisis parmi n, sans tenir compte de l’ordre.

`itertools.combinations` ne renvoie pas une liste : c’est un itérateur

Lorsque l’on utilise itertools.combinations, il est tentant de penser que la fonction renvoie immédiatement une liste contenant toutes les combinaisons possibles. Ce n’est pas le cas. L’appel :

from itertools import combinations
comb = combinations([1, 2, 3, 4], 2)

ne construit pas en mémoire toutes les paires possibles. Il renvoie un objet itérateur, c’est-à-dire un objet capable de produire les combinaisons au fur et à mesure, uniquement lorsqu’elles sont demandées.

Si l’on affiche directement l’objet :

print(comb)

Python renvoie quelque chose comme :

>>> # script executed
<itertools.combinations object at 0x1164f90>
>>>

Tester dans le Bac à sable Python!

Cela signifie que l’on dispose d’un générateur de combinaisons, et non d’une collection déjà matérialisée.

Pourquoi un itérateur et non une liste ?

Ce choix n’est pas anodin. Il est directement lié à la nature combinatoire du problème.

Le nombre de combinaisons de p éléments parmi n est donné par
[katex]C_n^p[/katex].

Or cette quantité peut devenir extrêmement grande lorsque $n$ n augmente. Générer toutes les combinaisons et les stocker en mémoire pourrait devenir coûteux, voire impossible.

Un itérateur adopte une stratégie dite lazy (évaluation paresseuse) :

une combinaison est calculée,
elle est transmise au programme,
puis la suivante est calculée uniquement si nécessaire.

Ainsi, la mémoire utilisée reste minimale.

Conséquence pratique : parcours progressif

L’utilisation naturelle d’un objet combinations se fait dans une boucle :

from itertools import combinations — Logigramme fabriqué avec LOGIGW

from itertools import combinations

for a, b in combinations([1, 2, 3, 4], 2):
    print(a, b)

Les paires sont produites successivement. À aucun moment l’ensemble des combinaisons n’est stocké dans une liste complète.

Cette approche présente un avantage important : si l’on cherche une combinaison vérifiant une condition donnée, il est possible d’interrompre le parcours dès que le résultat est trouvé :

from itertools import combinations

nums = [2, 7, 11, 15, 3, 6]
for a, b in combinations(nums, 2):
    if a + b == 9:
        print(a, b)
        break

Dans ce cas, seules les combinaisons nécessaires sont générées.

⚠ Un itérateur se consomme

Un point essentiel doit être souligné : un itérateur ne peut être parcouru qu’une seule fois.

from itertools import combinations

c = combinations([1, 2, 3, 4], 2)

print(list(c))   # première conversion
print(list(c))   # seconde conversion

La seconde conversion renverra une liste vide. L’itérateur a été “épuisé” lors du premier parcours.

Tester dans le Bac à sable Python!

Si plusieurs parcours sont nécessaires, il convient soit de recréer l’itérateur, soit de convertir explicitement le résultat en liste — à condition que le volume de données reste raisonnable :

pairs = list(combinations([1, 2, 3, 4], 2))

Itérateur et combinatoire : une cohérence conceptuelle

Il existe une cohérence profonde entre la notion mathématique de combinaison et l’implémentation choisie par Python.

Le coefficient combinatoire [katex]C_n^p[/katex] peut croître très rapidement. En conséquence, une approche “en flux” est souvent plus pertinente qu’une approche fondée sur le stockage intégral des résultats.

itertools.combinations ne fournit donc pas une liste prête à l’emploi, mais un mécanisme de génération contrôlée. Ce choix reflète une philosophie plus large de Python : privilégier l’efficacité mémoire et la modularité des traitements.

Exemple : générer les mains de poker sans `itertools` (version lourde)

Au Texas Hold'em No Limit, vous recevez 2 cartes privatives.

Supposons que l’on représente le paquet par les entiers de 0 à 51.

Sans itertools, on peut écrire deux boucles imbriquées pour représenter ces cartes privatives possibles :

deck = list(range(52))

hands = []

for i in range(len(deck)):
    for j in range(i + 1, len(deck)):
        hands.append((deck[i], deck[j]))

print(len(hands))  # 1326

Tester dans le Bac à sable Python!

Ici :

toutes les 1326 mains sont construites,
elles sont stockées dans la liste hands,
la mémoire contient simultanément toutes les combinaisons.

Cette méthode fonctionne, mais :

elle construit explicitement la liste complète,
elle demande d’écrire la logique d’évitement des doublons (j = i + 1),
elle devient très lourde si le nombre de cartes augmente (5 cartes par exemple).

itertools.combinations et mains privatives au poker holdhem

Version avec `itertools.combinations` (version légère)

La même opération peut s’écrire :

from itertools import combinations

deck = range(52)

for hand in combinations(deck, 2):
    print(hand)

Différence fondamentale :

aucune liste complète n’est créée,
chaque main est produite une par une,
la mémoire reste minimale.

Si l’on souhaite simplement connaître le nombre total :

count = 0
for _ in combinations(deck, 2):
    count += 1

print(count)  # 1326

Le résultat est identique, mais sans stockage massif.

Pourquoi la différence devient spectaculaire avec 5 cartes

Pour une main complète de 5 cartes :

[katex]C_{52}^5[/katex]

soit 2 598 960 combinaisons.

La version “lourde” devrait créer une liste contenant plus de 2,5 millions de tuples :

hands = list(combinations(range(52), 5))

Cela représente plusieurs dizaines de mégaoctets en mémoire.

En revanche, l’itérateur :

for hand in combinations(range(52), 5):
    # analyse statistique
    pass

ne conserve qu’une seule combinaison à la fois.

En résumé

Sans itertools :

on construit explicitement toutes les mains,
on les stocke,
la mémoire croît avec le nombre de combinaisons.

Avec itertools.combinations :

on délègue la génération à un itérateur,
les mains sont produites à la demande,
la mémoire reste stable, même lorsque le nombre de combinaisons explose.

Dans un contexte combinatoire comme le poker, où les quantités passent rapidement de 1326 à plusieurs millions, cette différence n’est pas anecdotique : elle est structurelle.

Personnellement :

La première fois que j’ai utilisé itertools.combinations — encore avec une certaine hésitation — c’était lors de la génération des mains pour l'a page'application Poker Training de site2wouf.fr.

À ce moment-là, l’objectif était simplement pratique : produire proprement toutes les mains possibles sans écrire des boucles imbriquées interminables. Ce n’est qu’ensuite que la portée conceptuelle est devenue évidente. Derrière une ligne de code concise se cachait une idée mathématique ancienne : la combinatoire.

Ce qui paraissait être un simple outil Python révélait en réalité une cohérence profonde entre la théorie et l’implémentation. Générer des mains de poker revient exactement à parcourir les [katex]C_{52}^2[/katex] combinaisons possibles. Python ne faisait que traduire, de manière élégante, une formule déjà connue.

Avec un peu de recul, cette première utilisation a marqué un déclic : combinations n’est pas seulement pratique, il incarne une manière plus rigoureuse de penser les problèmes. Plutôt que de “fabriquer des listes”, il invite à raisonner en termes de génération contrôlée, de flux, et d’efficacité.

C’est précisément là que les mathématiques et la programmation cessent d’être deux mondes distincts pour devenir deux expressions d’une même idée.

Quand la mécanique masque l’idée

Imaginons que l’on souhaite former tous les groupes possibles de 3 élèves parmi une classe de 20.

itertools.combinations et groupe de 3 élèves

students = [
    "Alice", "Mohamed", "Sofia", "Lucas", "Yuki",
    "Amina", "Ethan", "Fatou", "Mateo", "Inès",
    "Noah", "Lina", "Arjun", "Chloé", "Ibrahim",
    "Maya", "Diego", "Leïla", "Hugo", "Zara"
]

groups = []

for i in range(len(students)):
    for j in range(i + 1, len(students)):
        for k in range(j + 1, len(students)):
            groups.append((students[i], students[j], students[k]))

print(len(groups))

Tester dans le Bac à sable Python!

Ce programme fonctionne.

Mais plusieurs éléments apparaissent immédiatement :

la structure repose sur trois boucles imbriquées ;
les prénoms ne sont jamais manipulés directement ;
le code parle d’indices (i, j, k) plutôt que d’élèves.

Autrement dit, la mécanique de parcours prend le pas sur l’idée mathématique.

Et si l’on décide de former des groupes de 4 élèves, il faut ajouter une quatrième boucle.
La structure du code devient dépendante de la profondeur combinatoire.

La version abstraite

Avec itertools.combinations, la même idée s’écrit :

from itertools import combinations

students = [
    "Alice", "Mohamed", "Sofia", "Lucas", "Yuki",
    "Amina", "Ethan", "Fatou", "Mateo", "Inès",
    "Noah", "Lina", "Arjun", "Chloé", "Ibrahim",
    "Maya", "Diego", "Leïla", "Hugo", "Zara"
]

groups = combinations(students, 3)

print(len(list(groups)))

Tester dans le Bac à sable Python!

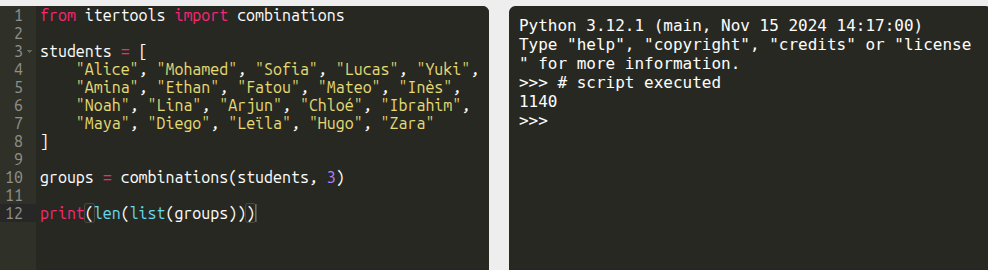
Ici :

aucune boucle imbriquée n’apparaît ;
aucun indice n’est manipulé ;
l’intention est explicite : “choisir 3 élèves parmi 20”.

Mathématiquement, le nombre de groupes possibles est :

[katex]C_{20}^3[/katex]

soit 1140 combinaisons.

La structure du code ne change pas si l’on passe à 4 élèves :

groups = combinations(students, 4)

Seul le paramètre varie.
La mécanique reste identiqu...

lien vers l'article sur wouf blog

TIPS

Un souci d'ortographe?

Sur le site de Wouf, Answers est directement accessible du menu en cliquant sur "liens". (dico)

Voir tous les conseils.

Dernière mise à jour:

Juillet-aôut 2023

Nouvelle Page !

Exercices du jour : Les 16 immeubles !

Pages modifiées (ou corrigées) !

Voir toutes les mises à jour.

Les conseils de Wouf

Quick Basic

NEWS

Des Mathématiques combinatoires avec Python et itertools.combinations

itertools.combinations ne renvoie pas une liste : c’est un itérateur

Pourquoi un itérateur et non une liste ?

Conséquence pratique : parcours progressif

⚠ Un itérateur se consomme

Itérateur et combinatoire : une cohérence conceptuelle

Exemple : générer les mains de poker sans itertools (version lourde)

Version avec itertools.combinations (version légère)

Pourquoi la différence devient spectaculaire avec 5 cartes

En résumé

Personnellement :

Quand la mécanique masque l’idée

La version abstraite

TIPS

Dernière mise à jour:

Nouvelle Page !

Pages modifiées (ou corrigées) !

`itertools.combinations` ne renvoie pas une liste : c’est un itérateur

Exemple : générer les mains de poker sans `itertools` (version lourde)

Version avec `itertools.combinations` (version légère)