ll ne faut jamais juger les gens sur leurs fréquentations : Judas, par exemple, avait des amis irréprochables.
Verlaine (Nouveau design)
Boite à outils

A chaque fois que l´on a un problème sur un pc, on regrette de ne pas avoir sauvegardé ses fichiers importants sur un support vraiment sûr. Mais en existe-t-il ?
C´est pourquoi j´ai décidé de placer ici, sur la toile, des liens vers des inclassables importants, freeware pour la plupart, à la disposition de tous et de chacun...

Les télécharger implique nécessairement de respecter les copyrights, et les lois des différents états, je ne saurais être tenu pour responsable d´une utilisation abusive, frauduleuse, ou illicite de l´un de ces produits.
Si vous désirez des informations sur les logiciels exposés, n'hésitez pas à commenter :
- Suite Bureautique:
- Archiveurs:
- Gestion d'images:
- Lecteurs Multimédia
- Synchronisation :
- L'image...
- CPP
- Python
- Quickbasic
- Editeur de script
- Naviguateur:
- Courrieleur:
- Client FTP:
- Editeur html:
NEWS
- Page : https://site2wouf.fr/tele.php
- Catégorie : Informatique
« Du jeu “saute-mouton” à l’algorithmique moderne »

Quand un jeu de 1980 contenait déjà les bases de l’algorithmique actuelle
Depuis plusieurs années, je conserve précieusement une collection de la revue Jeux & Stratégie. Ces magazines, publiés au début des années 1980 (J'avais à peine 13 ans), témoignent d’une époque charnière où les mathématiques, les jeux et l’informatique commençaient à se rencontrer dans le grand public.
On y parle aussi bien d’échecs que de logique, de probabilités, de programmation… parfois sur de simples calculatrices programmables.
En feuilletant un numéro de janvier 1980, je suis retombé sur un article qui mérite, à mon sens, une seconde vie :
Texte extrait de la revue Jeux & Stratégie, janvier 1980 (Jean-Jacques Dhenin).
Hier, l’ordinateur était un monstre d’un prix vertigineux que seuls des spécialistes pouvaient utiliser. Aujourd’hui, un amateur passionné peut s’acheter un « micro » pour quelque 6 000 francs et dialoguer avec lui après quelques heures d’entraînement. Totalement vulgarisé, l’ordinateur sera demain dans tous les foyers. Comptable, gardien ou secrétaire infatigable, on a assez dit qu’il s’acquittera de toutes les tâches ingrates. Nous préférons ici l’envisager comme un élément de loisir et, bien sûr, un partenaire de jeu.
En attendant qu’un large public dispose d’un tel matériel, nous vous présenterons dans cette rubrique des programmes de jeux pour des calculatrices de poche évoluées. Nous avons choisi pour l’instant des machines « haut de gamme » : la Hewlett-Packard HP-67 et la Texas Instruments TI-59. Encore chères, de 1 500 à 2 000 francs, elles offrent en effet de très larges possibilités et notamment des cartes magnétiques qui permettent de se constituer une bibliothèque de programmes.
Nous vous proposons même ici un programme pour la dernière née de Hewlett-Packard, la HP-41C, qui présente déjà de nombreux avantages propres aux ordinateurs, dont une imprimante et un affichage alphanumérique (lettres et chiffres).
À présent, à vous de jouer. Nous espérons que vous deviendrez vite des experts en « ludotique » et nous attendons avec impatience vos remarques… et vos programmes.
Jouez à saute-mouton

Comment faire passer les moutons de gauche à droite, et les moutons de droite à gauche ? Un mouton peut avancer sur une case vide ou sauter par-dessus un autre mouton de manière à retomber sur une case vide. Il ne peut en aucun cas reculer ni sauter par-dessus plusieurs moutons.
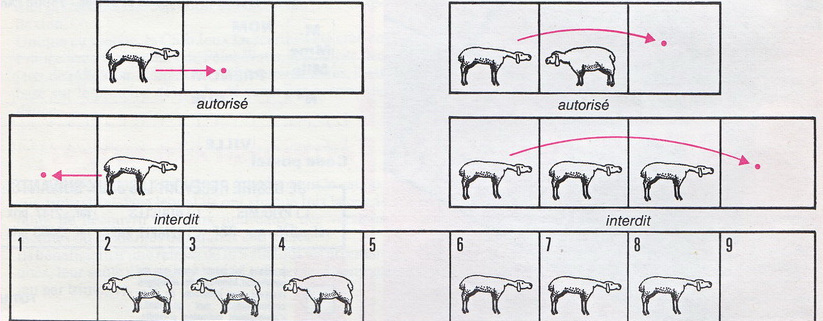
Pour cette première rubrique, vous ne jouerez pas vraiment contre les programmes, mais ils vous permettront de vous exercer agréablement à un joli casse-tête : le « saute-mouton ».
À votre gauche, les trois « 1 » représentent trois moutons bien maigres. À votre droite, les trois « 2 » sont des moutons bien gras. Chaque zéro indique une place vide, juste suffisante pour un mouton.
Ces petites bêtes se sont retrouvées face à face sur un sentier de montagne ; les trois moutons de gauche allant vers la droite et leurs congénères dans le sens opposé. Depuis l’histoire de Panurge, si ce n’est plus tôt, on sait leur caractère : ils peuvent avancer, sauter… mais jamais reculer.
Il vous appartient de permettre aux moutons de passer leur chemin sans encombre. Pour cela, il vous suffira d’indiquer le numéro de la case où se trouve le mouton que vous voulez voir se déplacer. En cas de manœuvre illégale, le programme redonne l’affichage de la situation sans modification.
La suite de l’article présentait le programme complet pour calculatrices programmables, que je n’ai volontairement pas reproduit ici.
Ce qui frappe à la lecture de cet article, plus de quarante ans plus tard, ce n’est pas seulement le matériel utilisé TI 59 ou HP 67, mais la démarche. Derrière ce jeu de moutons se cachent déjà des notions très modernes : état, règle de transition, coup légal, situation gagnante ou bloquée. Autrement dit, de l’algorithmique à l’état pur.
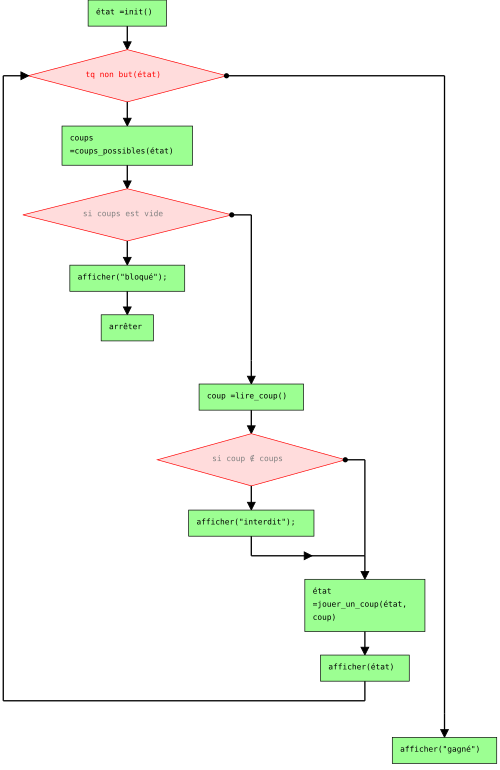
Logigramme généré automatiquement par logigw
Et le code
Une fois le fonctionnement du jeu formalisé sous forme de logigramme, sa traduction en code devient presque naturelle.
Dans les années 1980, cette logique était déjà mise en œuvre sur des calculatrices programmables, avec une mémoire limitée et un affichage minimal, ce qui imposait une écriture extrêmement rigoureuse.
LBL A ; initialisation 0 STO 0 ; case 0 (bord gauche) 1 STO 1 1 STO 2 1 STO 3 0 STO 4 ; case centrale vide 2 STO 5 2 STO 6 2 STO 7 0 STO 8 ; case 8 (bord droit) RTN
Aujourd’hui, en Python, la représentation de l’état du jeu par une simple liste permet un code lisible et proche du raisonnement humain.
# 0 : case vide # 1 : mouton allant vers la droite # 2 : mouton allant vers la gauche etat = [0,1, 1, 1, 0, 2, 2, 2,0]
En JavaScript, la même logique s’applique, avec en plus l’interaction directe à l’écran. Les outils ont évolué, mais l’algorithme reste le même : seule sa traduction change selon le support.
// 0 : case vide // 1 : mouton allant vers la droite // 2 : mouton allant vers la gauche let etat = [1, 1, 1, 0, 2, 2, 2];
Cliquez sur l'image pour jouer avec cette application sur le site2wouf.fr :

Et regardez moi jouer !
TIPS

Par pitié, Webmasters, ne cassez pas le bouton retour en usant et abusant de l'attribut target="_blank" en rédigeant vos liens!




