Les conseils de Wouf
Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.
Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.
Quand on ne sait pas, on a peur.
TIPS : conseils et astuces
Pour un surf correct, sur le site de Wouf, il vous faut avoir un navigateur de moins de 10 ans et ne pas refuser le javascript.
Si vous detectez une imperfection, n'hésitez pas à commenter!
Firefox est un très bon navigateur alternatif!
Lien de téléchargement dans la boite à outils du menu informatique...
Par pitié, Webmasters, ne cassez pas le bouton retour en usant et abusant de l'attribut target="_blank" en rédigeant vos liens!
Wikipedia l'encyclopédie libre, symbolise pour moi l'avenir du bon web.
Sur le site de Wouf, Wikipedia est accessible directement dans le menu "liens".
Et pourquoi pas le Site de Wouf comme page de démarrage sur Internet?
Une page légère et simple, avec des liens, des infos, des conseils, un peu de culture... Que demander de plus!
Gardez Windows propre!
Un lien vers Ccleaner est disponible dans la boite à outils, du menu "informatique"...
Testez votre FAI (Fournisseur d'Accés à Internet)...
Grenouille.com est accessible, par le menu, en cliquant sur "liens" puis "Plus!!!"
Un souci d'ortographe?
Sur le site de Wouf, Answers est directement accessible du menu en cliquant sur "liens". (dico)
A qui appartient ce numéro de téléphone?
www.ctqui.com offre un service gratuit: il répond à cette question!
Cliquez sur "Liens" puis sur "Plus!!!"
Perdu l'annuaire?
www.annu.com est accessible sur le site de Wouf, par l'intermédiaire du menu "Liens" en cliquant sur "Plus"
|
Dingue de télé? Demandez le programme, dans le menu "liens"... |
CommentCaMArche.net, encyclopédie libre.
Ce site est une mine d'informations accessibles, d'ici en cliquant sur "Liens" puis "Plus!!!"
Connaissez-vous OOO?.
Open Office (.Org) est une suite bureautique pleine d'avenir, avec déjà un passé riche.
Traitement de texte, tableur, gestionnaire de base de données, etc... Rien ne manque!
Open office est indispensable, un lien vers le site de téléchargement est bien rangé, dans la boite à outil du menu "Informatique".
Connaissez-vous VLC media player?
Ce petit logiciel est un lecteur multimédia qui lit presque tous les formats!
Un lien pour télécharger ce petit bijou?
Oui! dans la boite à outil du menu "Informatique"
UN T-shirt ou une doudoune demain?
meteofrance est joignable en cliquant sur "Liens".
Vous cherchez un logiciel gratuit?
est joignable en cliquant sur "Liens" puis sur "Plus".
Perdu l'annuaire?
www.118218.fr est accessible sur le site de Wouf, par l'intermédiaire du menu "Liens" en cliquant sur "Annuaire"
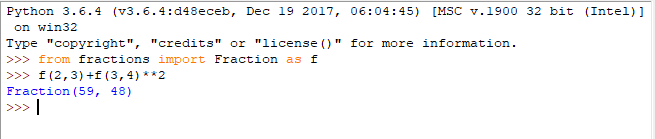
Vous connaissez Python?
Python est un langage de programmation.
Le nom Python ne viendrait pas du nom d'un reptile mais du Monty Python Flying Circus, un groupe de comiques complètement déjantés qui ont sévis sur la BBC dans les années 60-70.
Sur le site de Wouf, vous trouverez:
- Un lien de téléchargement dans la boite à outil du menu informatique.
- Des liens vers des didacticiels et aides en ligne dans le menu Liens "Plus"
- Un exemple de sources là
Python is fantastic!
Allhtml est plus qu'un site, c'est une communauté de passionnés en développement web.
Sur le site de Wouf, AllHtml est accéssible en cliquant sur liens puis "plus"
Sur le site de Wouf, dans le menu "lien", en survolant "wikipedia", apparaît l'item: "Une page au hasard".
Par un simple clique, on accède à une page de Wikipedia... au hasard!
Un moyen original de se cultiver...
Besoin d'afficher un diagramme d'Echecs, sans héberger forcément l'image ?
Chessdiag.org est fait pour vous !
Navigateur Web Opera
Le navigateur le plus rapide au monde !
Naviguez sur le Web à la vitesse de l'éclair. Découvrez le nouveau design élégant et les nombreuses autres améliorations d'Opera.
http://www.opera.com/
Avez-vous vu les fonds d'écran du menu informatique/goodies ?
Développé par Laurens Koppers, ce site classroomscreen.com peut être un incontournable en classe ! Je vous recommande une visite !
Pearltrees est un service web qui permet d'organiser, d'explorer et de partager des contenus numériques.
Un lien se vers Pearltrees se trouve dans le menu info>liens>
Mon Pearltress : https://www.pearltrees.com/wouf
FullSync est un utilitaire de synchronisation et de sauvegarde de fichiers personnalisable. publié sous licence GNU GPL.
Plus d'information sur le blog
NEWS
- Page : https://site2wouf.fr/tips.php
- Catégorie : Informatique
Les Principales IA Disponibles classée par thèmes
Dans cet article, nous vous présentons un aperçu des IA les plus innovantes et influentes qui façonnent notre quotidien. Cependant, le monde de l'IA évolue à une vitesse fulgurante, et de nouvelles solutions émergent constamment. Nous aimerions connaître votre avis : quelles autres IA trouvez-vous prometteuses ou révolutionnaires ? Partagez vos découvertes et suggestions dans les commentaires pour enrichir notre discussion et rester à la pointe de cette technologie fascinante !
Modèles de Langage Généraux
- ChatGPT - Le chatbot d'OpenAI basé sur GPT-4
- Claude - L'assistant IA d'Anthropic
- Gemini - L'IA conversationnelle de Google
- Perplexity AI - Moteur de recherche alimenté par l'IA
- Le Chat - L'assistant IA de Mistral AI, basé sur Mistral-7B
IA Créatives et Artistiques
- Midjourney - Génération d'images artistiques
- DALL-E 3 - Création d'images par OpenAI
- Stable Diffusion - Génération d'images open source
- Runway - Création et édition vidéo par IA
Outils Spécialisés
- GitHub Copilot - Assistant de programmation
- Jasper - Rédaction assistée par IA
- Copy.ai - Création de contenu marketing
- Grammarly - Correction et amélioration de texte
- Jouer aux échecs contre l'une des meilleures IA en ligne
- Jouer contre une IA en ligne (pour le fun)
IA pour la Science et l'Éducation
- Wolfram Alpha - Calculs et analyses scientifiques
- Khan Academy - Plateforme d'apprentissage en ligne (Khanmigo intégré)
- DeepMind - Recherche IA avancée en biologie et mathématiques
Assistants Vocaux
- Alexa - L'assistant vocal d'Amazon
- Google Assistant - Assistant intelligent de Google
- Siri - Assistant vocal d'Apple
TIPS
Vous connaissez Python?
Python est un langage de programmation.
Le nom Python ne viendrait pas du nom d'un reptile mais du Monty Python Flying Circus, un groupe de comiques complètement déjantés qui ont sévis sur la BBC dans les années 60-70.
Sur le site de Wouf, vous trouverez:
- Un lien de téléchargement dans la boite à outil du menu informatique.
- Des liens vers des didacticiels et aides en ligne dans le menu Liens "Plus"
- Un exemple de sources là
Python is fantastic!