Les conseils de Wouf
Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.
Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.
Les courses, pour reprendre le slogan célèbre, c'est ma grande passion...
Mais gagner de l'argent aux courses, en pariant sur des résultats assez aléatoire est risqué, même si le frisson est au rendez-vous.
Le but de chaque turfiste est de tenter de maîtriser le hasard.
PPP était un utilitaire d'aide à la prise de paris PMU.
Le raisonnement ensembliste:
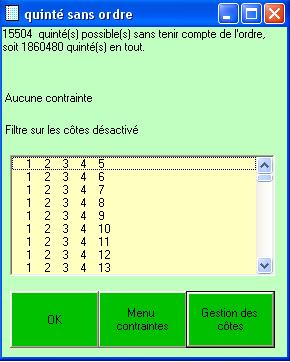
20 est le nombres maximum de partants dans une course servant de support au quinté+. Cela donne 15504 quintés possibles si on ne tient pas compte de l'ordre. Les jouer tous est sinon impossible du moins assez idiot.
Mais il est parfois possible de restreindre ces combinaisons par des "contraintes": Supposons que les 8 premiers favoris de la presse sont 1,2,3,4,5,6,7,8 alors une contrainte comme :
- au moins 3 chevaux dans 1,2,3,4,5,6,7,8 est raisonnable et limite considérablement le nombres de "quintés possibles".
Supposons que les numéros 1,8,9,10,11 soient des femelles et que ces mêmes femelles ne réussissent habituellement pas dans le passé de cette course on utilisera (par exemple) la contrainte:
- au plus 1 cheval dans 1,8,9,10,11...
L'expérience de chacun lui permet de trouver les contraintes les plus efficaces.
La vocation de PPP
La vocation de PPP est de gérer un grand nombres de contraintes ensemblistes de ce genre, c'est infaisable à la main!
Remarque
Je développe actuellement la deuxième mouture de PPP, qui gardera le même moteur, mais en liaison avec un base de donnée. PPP sera alors capable d'inventer des contraintes adaptées à un évenement hippique particulier.
Avec une contrainte du genre "au plus un cheval dans les huit premiers favoris de la presse", le prix Rieussec ne mettra peut-être plus le parieur à sec.
Le développement est long et difficile, repassez me voir ;-)
NEWS
- Page : https://site2wouf.fr/ppp.php
- Catégorie : Non définie
IA à l’École : ce que l’Inspection générale va observer en 2026-2027
De l’expérimentation dispersée à l’évaluation institutionnelle
Jusqu’à présent, l’intelligence artificielle est surtout entrée dans les établissements scolaires par petites touches. Un professeur l’utilise pour reformuler une consigne, un autre pour préparer une activité différenciée, un personnel de direction pour synthétiser un document, tandis qu’une équipe expérimente un outil dans le cadre d’une formation ou d’un projet académique.
Ces pratiques existent, mais elles restent encore très inégales. Elles dépendent souvent de l’intérêt personnel des utilisateurs, de leur niveau de formation, des outils auxquels ils ont accès et du temps qu’ils peuvent consacrer à leur prise en main. D’un établissement à l’autre, voire d’une salle des professeurs à l’autre, la place de l’IA peut donc être très différente.
Une nouvelle étape
Le Bulletin officiel du 23 juillet 2026 marque à ce titre une nouvelle étape. Dans son programme de travail pour l’année scolaire 2026-2027, l’Inspection générale de l’éducation, du sport et de la recherche reçoit une mission consacrée à l’« évolution des usages pédagogiques et administratifs de l’intelligence artificielle dans les établissements scolaires ».
Le choix du mot évolution est important. L’institution ne se demande plus seulement si l’IA va entrer à l’École : elle considère que cette entrée a déjà commencé. Il s’agit désormais d’observer ce qui se passe réellement sur le terrain, de mesurer la diffusion des usages et de mieux comprendre ce qu’ils transforment dans le travail quotidien des établissements.
Cette mission ne constitue donc pas une nouvelle réglementation imposée aux professeurs. Le texte ne rend aucun outil obligatoire, n’en interdit aucun nouveau et ne fixe pas de procédure particulière pour préparer un cours, corriger un travail ou utiliser une IA avec des élèves. Il annonce avant tout une démarche d’évaluation institutionnelle.
L’enjeu est de passer d’une multitude d’expériences individuelles, parfois intéressantes mais difficiles à comparer, à une vision plus globale. Quels usages se sont réellement installés ? Lesquels restent marginaux ? Quels bénéfices les enseignants en retirent-ils ? Quelles difficultés rencontrent-ils ? Les usages pédagogiques progressent-ils au même rythme que les usages administratifs ?
À travers cette mission, le ministère cherche donc à établir un nouvel état des lieux. Après le temps de la découverte et des expérimentations dispersées vient celui de l’observation organisée, des bilans et, probablement, des futures recommandations.
Autrement dit, l’IA n’est plus seulement un sujet dont quelques professeurs curieux discutent entre deux cours : elle devient un objet d’étude à part entière pour l’institution scolaire.
Quels usages pédagogiques et administratifs seront observés ?
Le Bulletin officiel distingue clairement deux grandes familles de pratiques : les usages pédagogiques et les usages administratifs de l’intelligence artificielle. Le texte ne fournit pas de liste détaillée, mais cette distinction permet déjà de comprendre l’étendue de la mission confiée à l’Inspection générale.
Les usages pédagogiques : de la préparation du cours aux apprentissages
Du côté pédagogique, l’IA peut intervenir bien avant l’entrée des élèves dans la salle de classe. Elle peut aider un professeur à chercher des idées d’activités, à reformuler une consigne, à adapter un document, à produire plusieurs versions d’un exercice ou à préparer des exemples correspondant à différents niveaux de maîtrise.
Elle peut également être mobilisée pendant les apprentissages. Certains enseignants l’utilisent comme point de départ pour exercer l’esprit critique : repérer une erreur, vérifier une réponse, comparer plusieurs raisonnements ou améliorer un texte produit automatiquement. Dans ce cas, l’IA n’est pas seulement un outil qui fournit une réponse : elle devient elle-même un objet d’analyse.
La différenciation devrait logiquement occuper une place importante dans l’étude. Une IA peut proposer une explication plus simple, générer un exemple supplémentaire, modifier le niveau de difficulté d’un exercice ou aider à préparer un support adapté à certains besoins. Ces possibilités sont séduisantes, mais elles soulèvent une question essentielle : l’outil améliore-t-il réellement les apprentissages ou donne-t-il seulement l’impression de faire gagner du temps ?
L’évaluation constitue un autre chantier incontournable. Comment concevoir un devoir lorsque les élèves peuvent obtenir en quelques secondes une rédaction, un programme informatique ou une résolution détaillée ? Comment distinguer l’aide ponctuelle de la substitution complète au travail attendu ? Et surtout, comment faire évoluer les consignes pour continuer à évaluer une compréhension, un raisonnement ou une démarche personnelle ?
Les usages administratifs : une face plus discrète de l’IA
Les usages administratifs sont moins visibles, mais probablement déjà très présents. L’IA peut être utilisée pour résumer un document, préparer un compte rendu, reformuler un courrier, structurer un projet, produire une trame de réunion ou extraire les idées principales d’un texte institutionnel.
Ces pratiques ne concernent pas uniquement les personnels de direction ou les services administratifs. Les professeurs consacrent eux aussi une part importante de leur temps à des tâches de rédaction, d’organisation et de communication : appréciations, bilans, projets, messages aux familles, documents de suivi ou comptes rendus de réunions.
L’Inspection générale pourrait donc s’intéresser au gain de temps réellement obtenu, mais aussi à la qualité des productions générées. Une synthèse peut sembler claire tout en oubliant une nuance importante. Un courrier peut être parfaitement rédigé tout en ne correspondant pas exactement à la situation. L’IA facilite la production d’un texte, mais elle ne garantit ni sa pertinence ni son exactitude.
Observer les usages, mais aussi leurs conditions
Étudier l’IA dans les établissements ne consistera probablement pas seulement à compter le nombre d’utilisateurs. Il faudra aussi comprendre dans quelles conditions les outils sont employés :
- avec quelle formation,
- quelles consignes,
- quelles vérifications
- quelles précautions concernant les données personnelles.
Deux professeurs peuvent en effet utiliser le même outil de manière très différente. L’un lui délègue presque entièrement la production d’une activité. L’autre s’en sert comme d’un brouillon qu’il relit, corrige et adapte soigneusement. Dans les deux cas, on parlera d’un usage de l’IA, mais la réalité pédagogique ne sera pas la même.
L’enjeu de la mission sera donc moins de savoir si l’IA est utilisée que de comprendre pourquoi, comment et avec quels effets elle l’est.
Former les personnels… et former ceux qui les formeront
Observer l’évolution des usages de l’intelligence artificielle dans les établissements est nécessaire. Mais cette observation n’aura de véritable portée que si elle débouche sur une politique de formation à la hauteur des transformations en cours.
Sur ce point, le diagnostic posé par l’Inspection générale en 2025 était déjà particulièrement clair. Dans son enquête, 75 % des enseignants interrogés désignaient le manque de formation comme un frein à l’intégration de l’IA dans leurs pratiques pédagogiques. La mission estimait par ailleurs qu’environ 10 % seulement des enseignants ayant répondu avaient bénéficié d’une formation.
Le problème ne semble donc pas être un manque d’intérêt. Il réside plutôt dans la difficulté à proposer une formation accessible, cohérente et suffisamment proche des réalités professionnelles. L’Inspection générale décrivait ainsi une offre encore dispersée, parfois peu lisible, très dépendante des initiatives locales et touchant souvent les personnels déjà les plus familiers du numérique.
Son rapport recommandait en conséquence une formation massive et coordonnée, dont la première étape se déroulerait en présentiel dans les établissements. Cette précision est importante. Un parcours en ligne, un webinaire ou un ensemble de ressources peuvent être utiles pour approfondir une réflexion déjà engagée. Ils remplacent plus difficilement un premier temps collectif permettant de manipuler les outils, de poser des questions, d’exprimer des réticences et de confronter les usages aux réalités d’une discipline ou d’un établissement.
Depuis ce premier état des lieux, l’offre s’est étoffée. Un parcours Pix+ Édu consacré à l’usage éclairé et responsable de l’IA générative est accessible sur Magistère. Le projet européen AI4T, « Intelligence artificielle pour et par les professeurs », propose également un MOOC et un manuel ouvert. Réseau Canopé, les DRANE et les académies développent de leur côté des formations, des ateliers et des ressources de plus en plus nombreuses.
Le Programme national de formation 2026-2027 confirme cette orientation. Son action consacrée à l’IA prévoit notamment de former des formateurs académiques, des référents numériques, des membres de la CREIA, des inspecteurs et des formateurs disciplinaires. Elle doit les aider à construire et à évaluer des scénarios pédagogiques intégrant l’IA, en articulant les enjeux transversaux avec les particularités de chaque discipline.
Cette formation des formateurs constitue un étage indispensable. On ne peut pas envisager de former plusieurs centaines de milliers de personnels sans s’appuyer sur des professionnels capables d’accompagner ensuite les équipes au plus près du terrain. Le Programme national de formation assume d’ailleurs explicitement cette logique de démultiplication : former des formateurs au niveau national pour permettre un déploiement dans les académies, puis dans les établissements.
Il faut néanmoins regarder cette organisation avec lucidité. Former les formateurs ne peut pas consister uniquement à leur présenter quelques outils récents ou à leur transmettre une collection de « bonnes invites » prêtes à l’emploi. Les services évoluent trop rapidement pour qu’une formation centrée sur une interface ou une marque conserve longtemps sa pertinence.
Un formateur doit pouvoir expliquer, sans discours magique ni simplification excessive,...
lien vers l'article sur wouf blogTIPS
Connaissez-vous VLC media player?
Ce petit logiciel est un lecteur multimédia qui lit presque tous les formats!
Un lien pour télécharger ce petit bijou?
Oui! dans la boite à outil du menu "Informatique"