Les conseils de Wouf
Beaucoup d’élèves entrant au lycée ont en effet des difficultés à manipuler les fractions, les racines carrées, les puissances, à factoriser des expressions… Ces notions, apprises au collège, sont mal assimilées, et le programme des classes de lycée ne prévoit pas de les retravailler en profondeur.
Cet ouvrage propose une remédiation pas à pas. Un code simple et mnémotechnique est associé à chacune des règles et rappelé dans toutes les corrections d’exercices. Il permet de se repérer et de comprendre ses erreurs.
Je suis un homme d'intérieur, toujours au comptoir, jamais en terrasse.
Jean-Jacques Peroni (sur mon T shirt!)
0 zéro 1 un 2 deux 3 trois 4 quatre 5 cinq 6 six 7 sept 8 huit 9 neuf 10 dix 11 onze 12 douze 13 treize 14 quatorze 15 quinze 16 seize 17 dix-sept 18 dix-huit 19 dix-neuf 20 vingt 21 vingt et un 22 vingt-deux 23 vingt-trois 24 vingt-quatre 25 vingt-cinq 26 vingt-six 27 vingt-sept 28 vingt-huit 29 vingt-neuf 30 trente 31 trente et un 32 trente-deux 33 trente-trois 34 trente-quatre 35 trente-cinq 36 trente-six 37 trente-sept 38 trente-huit 39 trente-neuf 40 quarante 41 quarante et un 42 quarante-deux 43 quarante-trois 44 quarante-quatre 45 quarante-cinq 46 quarante-six 47 quarante-sept 48 quarante-huit 49 quarante-neuf 50 cinquante 51 cinquante et un 52 cinquante-deux 53 cinquante-trois 54 cinquante-quatre 55 cinquante-cinq 56 cinquante-six 57 cinquante-sept 58 cinquante-huit 59 cinquante-neuf 60 soixante 61 soixante et un 62 soixante-deux 63 soixante-trois 64 soixante-quatre 65 soixante-cinq 66 soixante-six 67 soixante-sept 68 soixante-huit 69,soixante-neuf 70 soixante-dix 71 soixante et onze 72 soixante-douze 73 soixante-treize 74 soixante-quatorze 75 soixante-quinze 76 soixante-seize 77 soixante-dix-sept 78 soixante-dix-huit 79 soixante-dix-neuf 80 quatre-vingts 81 quatre-vingt-un 82 quatre-vingt-deux 83 quatre-vingt-trois 84 quatre-vingt-quatre 85 quatre-vingt-cinq 86 quatre-vingt-six 87 quatre-vingt-sept 88 quatre-vingt-huit 89 quatre-vingt-neuf 90 quatre-vingt-dix 91 quatre-vingt-onze 92 quatre-vingt-douze 93 quatre-vingt-treize 94 quatre-vingt-quatorze 95 quatre-vingt-quinze 96 quatre-vingt-seize 97 quatre-vingt-dix-sept 98 quatre-vingt-dix-huit 99 quatre-vingt-dix-neuf 100 cent
NEWS
- Page : https://site2wouf.fr/centpremiersnombres.php
- Catégorie : Non définie
Ce jeu est-il équitable ? Probabilité et arithmétique.
J'ai proposé à mes élèves de troisième, dans le devoir 12 de cette année scolaire (2024-2025) l’exercice suivant :
Exercice 2 (L’ utilisation d’un tableur est recommandée)
On donne le jeu suivant :
« Chacun des deux joueurs tire au hasard un nombre entier entre 1 et 100. Si les deux nombres
sont premiers entre eux, c’est le joueur A qui gagne, sinon, c’est le joueur B qui gagne. »
Le jeu est-il équitable ?
Mes objectifs pour cet exercice étaient nombreux :
- Travail sur des compétences arithmétiques (nombres premiers entre eux.)
- Travail sur des compétences probabilistes ( Dans une situation d'équiprobabilité)
- Travail sur des compétences algorithmiques (Tableur,Scratch, Python...)
- travail sur des compétences de "débrouillardise" (Recherche internet, IA)
On dit que deux nombres a et b sont premiers entre eux lorsque leur plus grand diviseur commun est égal à 1.
Erreurs et idées fausses.
L'erreur la plus fréquente dans les copies corrigées est assez classique : beaucoup d'élèves confondent "nombres premiers" (des nombres divisibles uniquement par 1 et eux-mêmes) et "nombres premiers entre eux" (voir la définition dans l'encadré ci-dessus).
Bien évidemment, deux nombres premiers sont toujours premiers entre eux, mais la réciproque est fausse : deux nombres peuvent être premiers entre eux sans être premiers.
Par exemple, 24 et 35 ne sont pas premiers (24 = 2 × 2 × 2 × 3 et 35 = 5 × 7), mais leur PGCD est 1, donc ils sont premiers entre eux.
Une erreur m'a interpellé :
Plusieurs élèves ont affirmé que le joueur A était avantagé parce que le nombre 1 est "premier avec tous les autres". L'intuition n'est pas totalement fausse, mais la formulation manque de rigueur, et surtout, elle ne suffit pas à conclure sur l’équité du jeu.
Il est vrai que le PGCD de 1 et n’importe quel autre nombre est toujours 1, donc si l’un des deux joueurs tire le nombre 1, le couple sera automatiquement premier entre eux, et A gagnera. Cela ajoute effectivement des cas favorables à A. Mais cela ne veut pas dire pour autant que le jeu est inéquitable uniquement à cause de ce cas particulier.
En réalité, pour savoir si le jeu est équitable, il faut compter précisément le nombre total de paires (a, b) avec a et b choisis entre 1 et 100, et déterminer dans combien de ces cas le PGCD(a, b) = 1. Ce n’est qu’en calculant la proportion de couples premiers entre eux qu’on peut trancher.
L’ utilisation d’un tableur est recommandée
C'est un travail conséquent qui nécessite des connaissance sur le tableur :
Remplir automatiquement des plages de cellules
(#128073#) Utiliser la poignée de recopie pour générer les nombres de 1 à 100 en ligne ou en colonne.
✅ Compétence de base pour structurer les données.
Créer un tableau à double entrée
(#128073#) Générer toutes les paires possibles (a, b) avec 1 ≤ a ≤ 100 et 1 ≤ b ≤ 100.
✅ Permet de représenter toutes les situations possibles du jeu.
Utiliser la fonction PGCD() ou GCD()
(#128073#) Pour chaque couple (a, b), calculer le PGCD.
✅ Fonction centrale pour savoir si les deux nombres sont premiers entre eux (PGCD = 1).
Utiliser une fonction conditionnelle (SI, IF)
(#128073#) Par exemple : =SI(PGCD(A1;B1)=1;1;0) pour compter les cas favorables à A.
✅ Utile pour automatiser le décompte des cas gagnants.
Compter avec NB.SI() ou SOMME()
(#128073#) Calculer le nombre total de cas favorables à A, et à B.
✅ Nécessaire pour comparer les proportions et juger de l’équité.
Calculer une proportion ou un pourcentage
(#128073#) Par exemple : =Nombre_de_cas_pour_A / Total_des_cas
✅ Permet d’estimer la probabilité de victoire de A.
Mise en forme conditionnelle (facultative)
(#128073#) Colorer en vert les cellules où A gagne, en rouge celles où B gagne.
✅ Offre une lecture visuelle intuitive des résultats.
Créer un graphique (facultatif)
(#128073#) Diagramme en secteurs ou histogramme pour visualiser les parts de victoire.
✅ Favorise la compréhension des résultats par l’élève.
Ma correction via Google sheets :
https://docs.google.com/spreadsheets/d/1xtw31iyetEezuk22H38nG_FMAwc1xv42RtPDuKV-kU4/edit?usp=sharing
De la mauvaise utilisation des IA
En effet si on livre l'exercice à ChatGPT, celui-ci nous répond :
Ce jeu n’est pas équitable.
Deux nombres entiers tirés au hasard entre 1 et 100 sont premiers entre eux s’ils n’ont pas de diviseur commun autre que 1, c’est-à-dire si leur PGCD vaut 1.
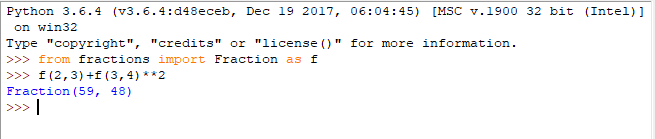
Il est connu en théorie des nombres que la probabilité que deux entiers choisis au hasard soient premiers entre eux est d’environ :
6 / π² ≈ 0,6079, soit 60,8 %.
Ainsi :
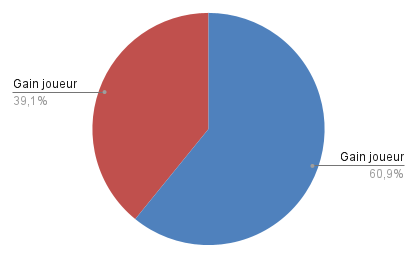
- Le joueur A gagne avec une probabilité d’environ 60,8 %.
- Le joueur B gagne avec une probabilité d’environ 39,2 %.
Même si ici les nombres sont limités de 1 à 100, cette probabilité reste proche de cette valeur. Le joueur A est donc avantagé.
Conclusion : le jeu n’est pas équitable.
Cette probabilité est issue d’un raisonnement en théorie des nombres et fait intervenir la fonction zêta de Riemann. La démonstration fait appel à :
- la densité des couples premiers entre eux (Théorème de Cesàro) parmi les entiers,
- la multiplicativité de la fonction indicatrice d’Euler,
- La série de Dirichlet.
La démonstration complète est un beau résultat de mathématiques pures, que l’on rencontre typiquement en licence ou début de master en mathématiques. Elle mêle analyse et arithmétique.
On est donc loin des attendus de troisième !
De la bonne utilisation des IA
Partager une passion est un privilège. Je développe en Python depuis Python 1.0 dans les années 90 et j'évoque ce langage souvent en classe. Par l’intermédiaire du bac à sable Python disponible sur le site2wouf.fr je montre qu'on peut, avec l'aide de Python et éventuellement d'une IA :
- s'amuser
- gagner du temps
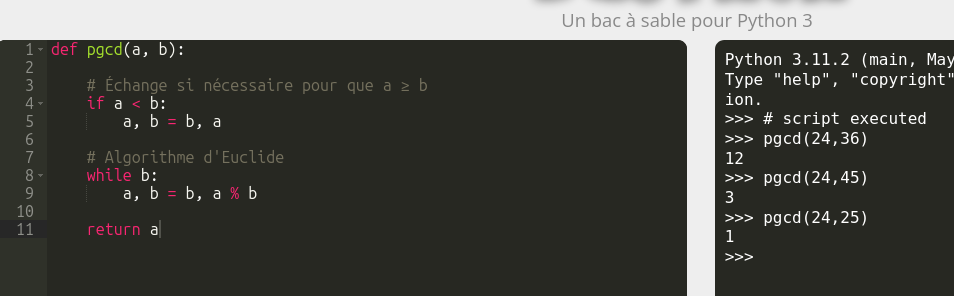
Ainsi quand on a évoqué les algorithmes de recherche du pgcd, j'ai donné cette fonction :
def pgcd(a, b):
# Échange si nécessaire pour que a ≥ b
if a < b:
a, b = b, a
# Algorithme d'Euclide
while b:
a, b = b, a % b
return a
N'hésitez pas à copier-coller dans le bac à sable !
Alors pourquoi ne pas simuler le jeu de l'exercice en utilisant cette fonction ?
from random import *
nb_max=100
score1=0
score2=0
def pgcd(a, b):
# Échange si nécessaire pour que a ≥ b
if a < b:
a, b = b, a
# Algorithme d'Euclide
while b:
a, b = b, a % b
return a
#-----------------------------------------------------
def jouer():
#les scores des joueurs sont des variables globales:
global score1,score2
j1,j2=randint(1,nb_max),randint(1,nb_max)
print("joueur 1 :",j1," joueur 2 :",j2)
if pgcd(j1,j2)==1:
score1+=1
else:
score2+=1
#---------------------------------------------------
for i in range(10): #on simule 10 parties
jouer()
if score1<score2:
print("Le joueur 2 a gagné !")
elif score1==score2:
print("Egalité !")
else:
print("Le joueur 1 a gagné !")
N'hésitez pas à copier-coller dans le bac à sable !
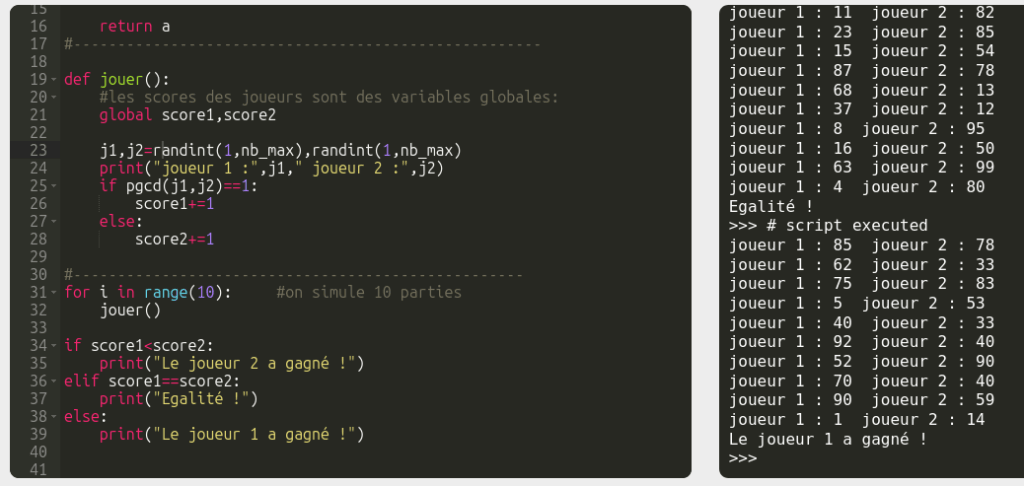
En répétant plusieurs fois l'exécution du script on a l'intuition que le joueur A gagne plus souvent que le joueur B. Mais ce n'est qu'une intuition.
Version finalisée
Plus besoin de hasard, on va tester tous les couples (sans rien afficher, il y en a 100x100=10 000) et livrer les résultats au sortir de la boucle :
score1=0
score2=0
def pgcd(a, b):
# Échange si nécessaire pour que a ≥ b
if a < b:
a, b = b, a
# Algorithme d'Euclide
while b:
a, b = b, a % b
return a
#-----------------------------------------------------
def jouer(j1,j2):
#les scores des joueurs sont des variables globales:
global score1,score2
if pgcd(j1,j2)==1:
score1+=1
else:
score2+=1
#---------------------------------------------------
for x in range(100):
for y in range(100): #x et y varient entre 0 et 99
jouer(x+1,y+1) #c'est pourquoi on ajoute 1
print("Les scores :",score1,score2)
print(score1/100,"% - ",score2/100,"%")
if score1<score2:
print("Le joueur 2 a plus de chance de gagner !")
elif score1==score2:
print("Le jeu est équitable")
else:
print("Le joueur 1 plus de chance de gagner !")
N'hésitez pas à copier-coller dans le bac à sable !
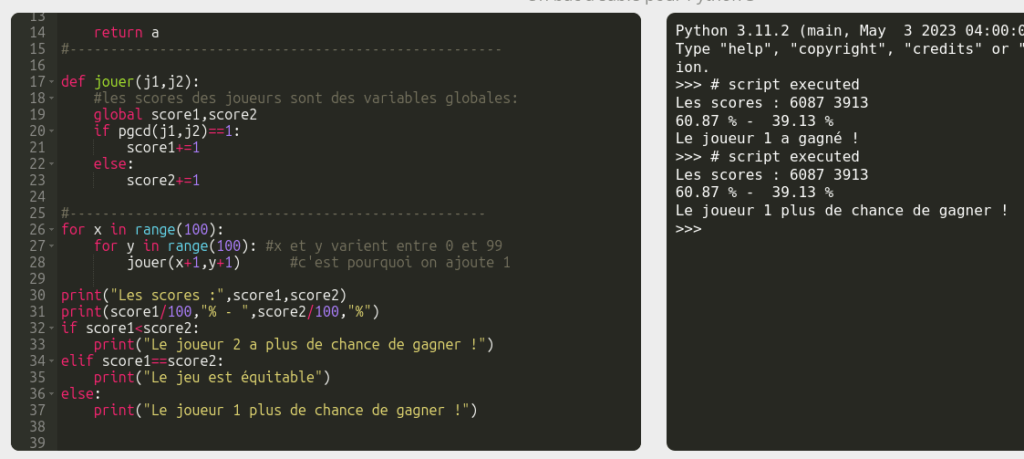
Nous avons le résultat en une fraction de seconde !
lien vers l'article sur wouf blog