Le djembé est à la musique ce que le couteau est à la purée.
1. Qu'est-ce qu'un algorithme ?
A. L'élève robot:
Instructions: Prog 1 Avance de 1 pas Répète tout 5 fois Inconvénient : On rigole quand l'élève est trop près du tableau ! Prog 2 Regarde devant Si tu peux avancer d'un pas alors : Avance de 1 pas Répète tout 5 fois
Ainsi, on peut voir un algorithme comme une suite d'instructions répétitives en interaction avec le monde extérieur.
B. Des exemples d'algorithmes :
- 1. La respiration est un algorithme lancé à la naissance par le cerveau reptilien, qui gère le fonctionnement de notre corps.
- INSPIRER
- SOUFFLER
- REPETER si nous sommes hors de l'eau
- Les machines distributrices de carburant
- etc.
2. Installation d Python 3.4
Au collège le MSI (programme destiné à l'installation sous Windows) est disponible sur le réseau dans P:\Math\Python. L'élève l'installe sur son poste, pour tous les utilisateurs (for all users). L'installation est aisée et rapide (next-next-next)
A noter : https://www.python.org/downloads/ est l adresse de téléchargement officiel.
3.Découverte de l'IDLE
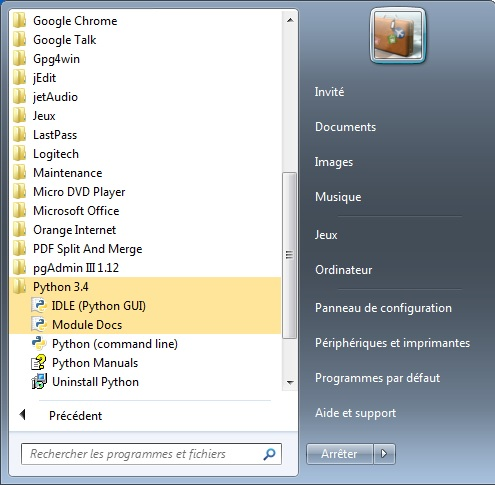
L IDLE est (entre autres) une super calculatrice :
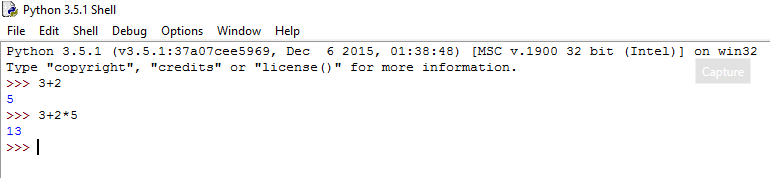
On peut remarquer que Python dans sa grande sagesse, respecte les priorités opératoires. Un avantage de ce super calculateur sur une calculatrice traditionnelle est la possibilité pour l'utilisateur de relire ses calculs, et de voir sur le même écran tous les résultats affichés simultanément.
Une objection d’élève et une solution élégante :
Sur une calculatrice on peut faire 10+5 EXE et elle affiche 15, puis faire *2 EXE et elle affiche 30, ça ne marche pas sous Python !!!
Si !
En utilisant l’opérateur « _ » (tiret du 8) :

Remarque (pas trop) intéressante
Python ne comprend pas tout ! Rien ne sert de lui dire bonjour !
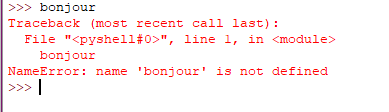
bonjour n’est pas défini : On va comprendre ce que cela veut dire !
4. 4. Première variable
Dans l'IDLE je demande aux élève de taper "exactement": prenom="Laurent" (En remplaçant Laurent par leur propre prénom !) Et d'appuyer sur ENTREE. La réponse de Python est étonnante pour les élèves : >>> Il ne se passe rien !
Que s'est-il donc passé ? Nous avons créé une variable prenom (sans majuscule, sans accent) qui peut être vue comme une boite en carton dans laquelle nous avons instantanément rangé quelque chose : une chaine de caractères (string).
Dans l'IDLE je demande alors aux élève de taper "exactement": print(10*prenom) Et avant d'appuyer sur ENTREE de tenter de deviner ce qui va se passer.
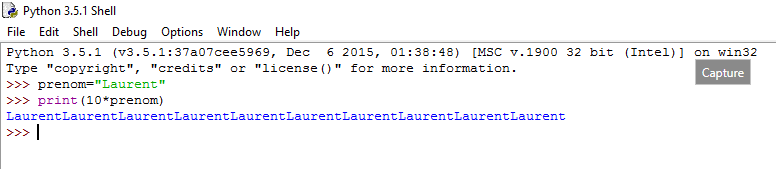
Remarque : une modification (presqu’) invisible
- autreprenom= « Robert \n »
- print(100*autreprenom)
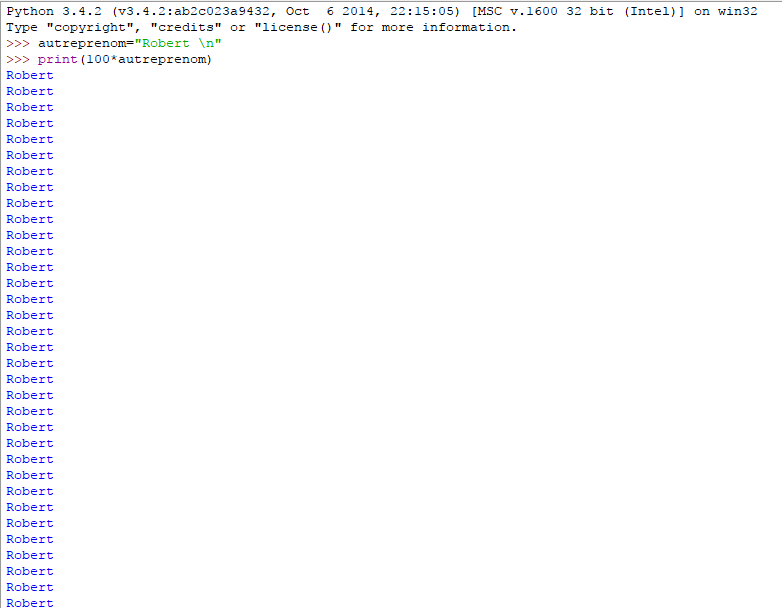
« \n » est un caractère non imprimable (qui ne s’affiche pas à l’écran) mais qui initie un passage à la ligne.
5. Premier programme vraiment utile (Exercice 1)
Je profite du mini chahut généré par cette dernière activité pour mimer une petite colère :<:p>
Vous me copierez 1000 fois : "Je ne dois pas parler en classe !" Hum … Oui vous pouvez utiliser Python !
Correction :
print(1000*"je ne dois pas parler en classe !")
Ou, plus joli :
print(1000*"je ne dois pas parler en classe ! \n")
6. Notion d’indices et casse-têtes
Dans l’IDLE je crée une variable mot : mot= « anticonstitutionnellement » et j’essaye successivement :
mot[2] ? affichage « t »
mot[5] ? affichage « o »
Exercice
Afficher avec cette syntaxe la lettre i puis la lettre a
Correction :
Ce qu’il faut comprendre c’est que pour Python la syntaxe mot[x] renvoie la lettre d’indice x, et que le premier indice est …zéro !
| Lettre | a | n | t | i | c | o | n | s | ... |
| Indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ... |
2 J’essaye maintenant :
mot[2 : 5] ? affichage « tic »
Exercice
et j’invite les élèves avec la même syntaxe à essayer d’afficher « cons »
Correction
La syntaxe mot[2 : 5] affiche les lettres d’indices 2 à 4 (lettre d’indice 5 : première lettre non affichée)
D’où : mot[4 : 8] ? affichage «cons »7
3 J’essaye maintenant :
mot[1 : 7 : 2] ? affichage «nio»
mot[1:7:-2] ? affichage «»
mot[7:1:-2] ? affichage «soi»
Exercice
Que signifie ce troisième nombre ?
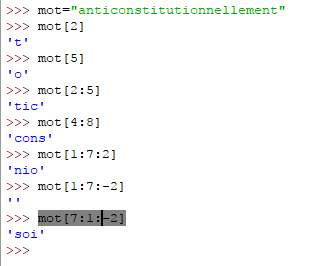
Remarque
Certaines valeurs peuvent être omises, essayez mot [5 :] mot[ :5] et mot[ ::-1] !

Au cycle 4, les élèves s'initient à la programmation, en développant dans une démarche de projet quelques programmes simples, sans viser une connaissance experte et exhaustive d'un langage ou d'un logiciel particulier. En créant un programme, ils développent des méthodes de programmation, revisitent les notions de variables et de fonctions sous une forme différente, et s'entraînent au raisonnement.
Attendus de fin de cycle
- Écrire, mettre au point et exécuter un programme simple
Connaissances et compétences associées
Décomposer un problème en sous-problèmes afin de structurer un programme ; reconnaître des schémas. Écrire, mettre au point (tester, corriger) et exécuter un programme en réponse à un problème donné. Écrire un programme dans lequel des actions sont déclenchées par des événements extérieurs. Programmer des scripts se déroulant en parallèle. - Notions d'algorithme et de programme. - Notion de variable informatique. - Déclenchement d'une action par un événement, séquences d'instructions, boucles, instructions conditionnelles.
Exemples de situations, d'activités et de ressources pour l'élève
Jeux dans un labyrinthe, jeu de Pong, bataille navale, jeu de nim, tic tac toe. Réalisation de figure à l'aide d'un logiciel de programmation pour consolider les notions de longueur et d'angle. Initiation au chiffrement (Morse, chiffre de César, code ASCII...). Construction de tables de conjugaison, de pluriels, jeu du cadavre exquis... Calculs simples de calendrier. Calculs de répertoire (recherche, recherche inversée...). Calculs de fréquences d'apparition de chaque lettre dans un texte pour distinguer sa langue d'origine : français, anglais, italien, etc.
Repères de progressivité:
En 5e, les élèves s'initient à la programmation événementielle. Progressivement, ils développent de nouvelles compétences, en programmant des actions en parallèle, en utilisant la notion de variable informatique, en découvrant les boucles et les instructions conditionnelles qui complètent les structures de contrôle liées aux événements.
- python.org Le site officiel, pour télécharger Python !
- Apprenez à programmer en Python avec Openclassrooms
- Un programme Python pour publier du code Python sur une page web
- Algorithme au cycle 4
- La séquence 1 : Qu'est-ce qu'un algorithme ? Où on joue avec les indices...
- La séquence 2 : Premier programme et premières boucles
- La séquence 3 : Premiers tests...
- La séquence 4 : Tests imbriqués.
- La séquence 5 : Premières fonctions.
- La séquence 6 : Bilan et commentaires
- La séquence 7 : Python et Cesar(1)
- La séquence 8 : Python et Cesar(2) : Un exemple de fonction récursive
- La séquence 9 : Python et Cesar(3) : Notion de portée de variable
- La séquence 10 : Python et Cesar(4) :boucle FOR et accès aux fichiers
- La Séquence 11 - Python, longueur et angle, le module turtle(1)
- Python sur le Blog
- Un exemple d'application utilisant tkinter : Juniper_U
- Scratch - site officiel
Blue-Bot est un robot autonome spécialement conçu pour une utilisation scolaire. Le robot : 125,00 €Pack 6 robots + station d'accueil : 759,00 €
- Le memo des séquences 1 et 2 en PDF
- Les sources :
- Bonjour monde !
- conjugueur.py version 0.0.0
- conjugueur.py version 0.0.1 (correction fin de séquence 2)
- conjugueur.py version 0.1.0 (fin de séquence 3)
- conjugueur.py version 0.2.0 (départ séquence 5)
- L'exemple de la séquence 3
- L'exemple de la séquence 3 (version corrigée)
- Les fonctions -projet cesar- de la séquence 9
NEWS
- Page : https://site2wouf.fr/algorithme_s1.php
- Catégorie : Informatique
« Du jeu “saute-mouton” à l’algorithmique moderne »

Quand un jeu de 1980 contenait déjà les bases de l’algorithmique actuelle
Depuis plusieurs années, je conserve précieusement une collection de la revue Jeux & Stratégie. Ces magazines, publiés au début des années 1980 (J'avais à peine 13 ans), témoignent d’une époque charnière où les mathématiques, les jeux et l’informatique commençaient à se rencontrer dans le grand public.
On y parle aussi bien d’échecs que de logique, de probabilités, de programmation… parfois sur de simples calculatrices programmables.
En feuilletant un numéro de janvier 1980, je suis retombé sur un article qui mérite, à mon sens, une seconde vie :
Texte extrait de la revue Jeux & Stratégie, janvier 1980 (Jean-Jacques Dhenin).
Hier, l’ordinateur était un monstre d’un prix vertigineux que seuls des spécialistes pouvaient utiliser. Aujourd’hui, un amateur passionné peut s’acheter un « micro » pour quelque 6 000 francs et dialoguer avec lui après quelques heures d’entraînement. Totalement vulgarisé, l’ordinateur sera demain dans tous les foyers. Comptable, gardien ou secrétaire infatigable, on a assez dit qu’il s’acquittera de toutes les tâches ingrates. Nous préférons ici l’envisager comme un élément de loisir et, bien sûr, un partenaire de jeu.
En attendant qu’un large public dispose d’un tel matériel, nous vous présenterons dans cette rubrique des programmes de jeux pour des calculatrices de poche évoluées. Nous avons choisi pour l’instant des machines « haut de gamme » : la Hewlett-Packard HP-67 et la Texas Instruments TI-59. Encore chères, de 1 500 à 2 000 francs, elles offrent en effet de très larges possibilités et notamment des cartes magnétiques qui permettent de se constituer une bibliothèque de programmes.
Nous vous proposons même ici un programme pour la dernière née de Hewlett-Packard, la HP-41C, qui présente déjà de nombreux avantages propres aux ordinateurs, dont une imprimante et un affichage alphanumérique (lettres et chiffres).
À présent, à vous de jouer. Nous espérons que vous deviendrez vite des experts en « ludotique » et nous attendons avec impatience vos remarques… et vos programmes.
Jouez à saute-mouton

Comment faire passer les moutons de gauche à droite, et les moutons de droite à gauche ? Un mouton peut avancer sur une case vide ou sauter par-dessus un autre mouton de manière à retomber sur une case vide. Il ne peut en aucun cas reculer ni sauter par-dessus plusieurs moutons.
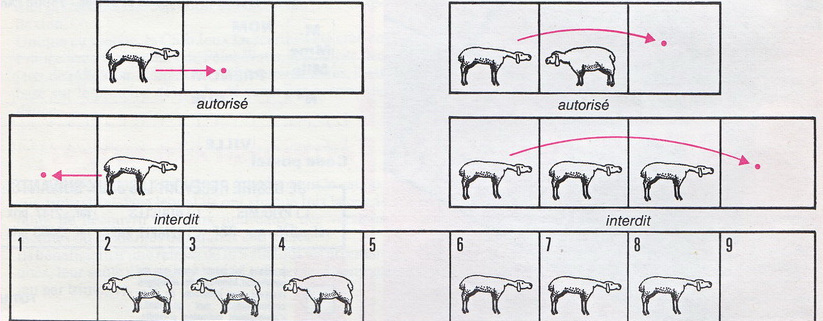
Pour cette première rubrique, vous ne jouerez pas vraiment contre les programmes, mais ils vous permettront de vous exercer agréablement à un joli casse-tête : le « saute-mouton ».
À votre gauche, les trois « 1 » représentent trois moutons bien maigres. À votre droite, les trois « 2 » sont des moutons bien gras. Chaque zéro indique une place vide, juste suffisante pour un mouton.
Ces petites bêtes se sont retrouvées face à face sur un sentier de montagne ; les trois moutons de gauche allant vers la droite et leurs congénères dans le sens opposé. Depuis l’histoire de Panurge, si ce n’est plus tôt, on sait leur caractère : ils peuvent avancer, sauter… mais jamais reculer.
Il vous appartient de permettre aux moutons de passer leur chemin sans encombre. Pour cela, il vous suffira d’indiquer le numéro de la case où se trouve le mouton que vous voulez voir se déplacer. En cas de manœuvre illégale, le programme redonne l’affichage de la situation sans modification.
La suite de l’article présentait le programme complet pour calculatrices programmables, que je n’ai volontairement pas reproduit ici.
Ce qui frappe à la lecture de cet article, plus de quarante ans plus tard, ce n’est pas seulement le matériel utilisé TI 59 ou HP 67, mais la démarche. Derrière ce jeu de moutons se cachent déjà des notions très modernes : état, règle de transition, coup légal, situation gagnante ou bloquée. Autrement dit, de l’algorithmique à l’état pur.
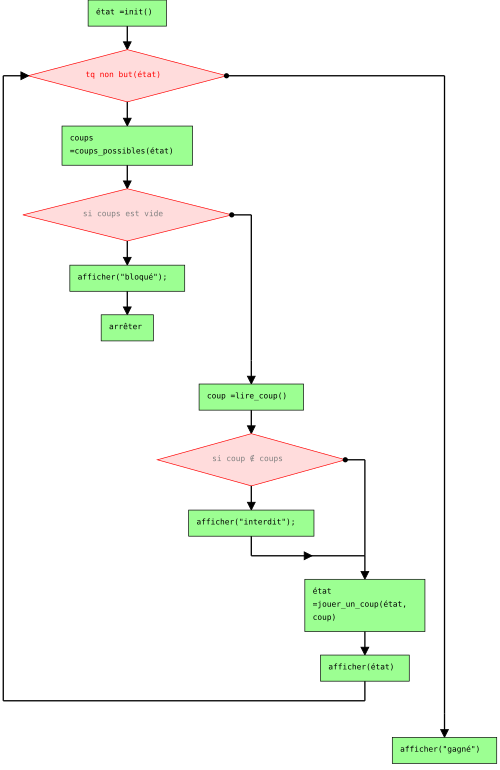
Logigramme généré automatiquement par logigw
Et le code
Une fois le fonctionnement du jeu formalisé sous forme de logigramme, sa traduction en code devient presque naturelle.
Dans les années 1980, cette logique était déjà mise en œuvre sur des calculatrices programmables, avec une mémoire limitée et un affichage minimal, ce qui imposait une écriture extrêmement rigoureuse.
LBL A ; initialisation 0 STO 0 ; case 0 (bord gauche) 1 STO 1 1 STO 2 1 STO 3 0 STO 4 ; case centrale vide 2 STO 5 2 STO 6 2 STO 7 0 STO 8 ; case 8 (bord droit) RTN
Aujourd’hui, en Python, la représentation de l’état du jeu par une simple liste permet un code lisible et proche du raisonnement humain.
# 0 : case vide # 1 : mouton allant vers la droite # 2 : mouton allant vers la gauche etat = [0,1, 1, 1, 0, 2, 2, 2,0]
En JavaScript, la même logique s’applique, avec en plus l’interaction directe à l’écran. Les outils ont évolué, mais l’algorithme reste le même : seule sa traduction change selon le support.
// 0 : case vide // 1 : mouton allant vers la droite // 2 : mouton allant vers la gauche let etat = [1, 1, 1, 0, 2, 2, 2];
Cliquez sur l'image pour jouer avec cette application sur le site2wouf.fr :

Et regardez moi jouer !
TIPS

Sur le site de Wouf, dans le menu "lien", en survolant "wikipedia", apparaît l'item: "Une page au hasard".
Par un simple clique, on accède à une page de Wikipedia... au hasard!
Un moyen original de se cultiver...





