Trimestre 1

Nombres entiers et Nombres rationnels

• Multiples et diviseurs - Critères de divisibilité par 2, 3, 5, 9 ou 10
• Effectuer une division euclidienne
• Racine carrée
• Notion de nombres premiers
• Décomposition en facteurs premiers
• Exploiter tableurs, calculatrices et logiciels

Étudier des problèmes d’engrenages (braquets d’un vélo, rapports de transmission d’une boîte de vitesses, horloge), de conjonction de phénomènes périodiques (éclipses ou alignements de planètes)

Déterminer deux fractions égales – Passer d’une représentation à une autre d’un nombre

Attendu de fin de cycle : Exemple de réussite

Deux ampoules clignotent. L’une s’allume toutes les 153 secondes et l’autre toutes les 187 secondes. À minuit, elles s’allument ensemble. Détermine l’heure à laquelle elles s’allumeront de nouveau ensemble

Liens

• Leçon
• Exercices – site2wouf.fr
• sesamath cycle4
• Algorithme et programmation : Autour du chat qui compte 

Notions retravaillées :

Priorités – Divisions - Nombres relatifs

Triangles et quadrilatères

• Utiliser les propriétés des angles et des triangles
• Les cas d'égalité de triangles
• Les triangles semblables
• Les quadrilatères
• Étudier des problèmes de pavage du plan.

Notions retravaillées :

Initiation à la démonstration – géométrie cycle 4

Attendu de fin de cycle : Exemple de réussite

Il réalise (à la main, à l’aide d’un logiciel de géométrie dynamique ou de programmation) la figure suivante obtenue à partir du triangle ABC par des rotations successives de centre A et d’angle 60° :

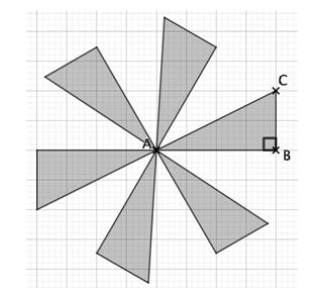
Il justifie que la figure précédente est composée de 6 triangles rectangles.

Liens

• Leçon
• Activité scratch sur les triangles d’après http://technocalvisi.free.fr/

Notions retravaillées :

Initiation à la démonstration – géométrie cycle 4

Le calcul numérique

• Priorité
• Relatifs
• Fractions
• Puissances
• Notation scientifique

Liens

• Leçon
• Exercices : Les relatifs
• Exercices : Fractions
• Exercices : Puissances
• Découverte du bac à sable Python

Notions retravaillées :

Relatifs - priorités - Ordre de grandeur – calcul littéral

Attendu de fin de cycle : Exemple de réussite

Une bactérie « se divise » en deux bactéries, chacune des deux bactéries obtenues « se partage » en deux nouvelles bactéries… Lorsque les conditions sont favorables, le nombre de bactéries peut être multiplié par deux toutes les trente minutes. Un chercheur place une bactérie en conditions favorables. Combien obtient-il de milliards de bactéries au bout de 18 h ?

Statistiques et probabilités

• Calculer et interpréter la moyenne simple ou pondérée d'une série statistique
• Calculer une médiane ou l'étendue d'une série statistique
• Modéliser une expérience aléatoire
• Calculer une probabilité
• Construire un arbre des probabilités

Liens :

• Leçon – site2wouf.fr
• Exercices statistiques
• Exercices probabilités
• Le module random de Python

Notions retravaillées :

Utilisation de tableur – Pourcentage

Attendu de fin de cycle : Exemples de réussite

Lecture de tableau et constructions de graphiques. Lecture de graphiques et calculs...

On suppose que, pour un couple, la probabilité d'avoir une fille ou un garçon est la même. Un couple souhaite avoir deux enfants.

• Calcule, en explicitant les issues possibles, la probabilité d’avoir deux garçons.
• -Calcule la probabilité que le couple ait au moins une fille.

Il peut utiliser le fait que c’est l’événement contraire d’avoir deux garçons.

Il utilise un logiciel de programmation pour réaliser la simulation d’une expérience aléatoire, par exemple : « Programmer un lutin pour qu’il énonce 100 nombres aléatoires « 0 » ou « 1 » et qu’il compte le nombre de « 0 » et de « 1 » obtenus. »

Trimestre 2

Le Triangle rectangle

• Le théorème de Pythagore et sa réciproque
• Les relations trigonométriques
• Calculer une longueur, la mesure d'un angle

Liens :

• Leçon : Le théorème de Pyhagore
• Leçon : Trigonométrie
• Exercices : Autour de Pyhagore
• Exercices : trigonométrie

Notions retravaillées :

Raisonnement – équation – les triangles semblables

Attendu de fin de cycle : Exemple de réussite

L'élève utilise les lignes trigonométriques dans un triangle rectangle pour calculer des longueurs ou des mesures d’angles

Le Calcul littéral

• Produire une écriture littérale
• Calculer une écriture littérale
• Développer et Factoriser une expression
• Vérifier si un nombre est solution d'équation ou d'inéquation
• Développer avec les identités remarquables
• Factoriser avec les identités remarquables
• Résoudre une équation « produit »
• Résoudre une inéquation
• Problèmes : Utiliser le calcul littéral pour prouver un résultat général, pour valider ou réfuter une conjecture.
• Programmes de calcul avec Python et Scratch

Liens :

• Leçon : Équations et inéquations
• Leçon :Calcul littéral
• Exercices : calcul littéral
• Exemples de résolutions d'équations commentés

Notions retravaillées :

Calcul littéral au cycle 4

Attendu de fin de cycle : Exemple de réussite

La facture d’eau d’un jardinier s’élève à 545 € par an. Il prévoit d'économiser 55 € par an en installant un récupérateur d'eau de pluie. Le récupérateur a coûté 199 € à l’achat et va nécessiter chaque année 13 € pour l'entretien (nettoyage, tuyau…). Au bout de combien d'années l’installation sera-t-elle rentable ?

Triangles et proportionnalité

• Reconnaître une situation de proportionnalité
• Calculer une 4eme proportionnelle
• Utiliser et calculer des pourcentages, des taux
• Grandeur produit, grandeur quotient
• Calculer une longueur avec le théorème de Thalès
• Justifier que deux droites ne sont pas parallèles
• Justifier que deux droites sont parallèles
• Reconnaître une réduction ou un agrandissement
• Calculer des longueurs réduites ou agrandies

Liens :

• Leçon : Le théorème de Thalès
• Exercices : Autour de Thalès

Notions retravaillées :

Raisonnement cycle 4 - Fractions - Équations - Ordre de grandeur - Arrondis

Attendu de fin de cycle : Exemple de réussite

L'élève utilise la proportionnalité pour calculer des longueurs dans une configuration de Thalès, dans des triangles semblables, dans le cadre des homothéties.

Trimestre 3

Notion de fonction

• Qu’est-ce qu’une fonction numérique ?
• Vocabulaire
• Les fonctions en Python et en scratch

Liens :

• Leçon : Notion de fonctions
• Une fonction en scratch

Notions retravaillées :

Équations simples – Calcul numérique

Attendu de fin de cycle : Exemples de réussite

Il sait que g(3) = 15 signifie que 15 est l’image de 3 par la fonction g et que 3 est un antécédent de 15 par la fonction g.

Il détermine l’image d’un nombre par une fonction à partir de son expression symbolique, de sa représentation graphique, d’un tableau de valeurs, d’un programme de calcul.

Grandeurs, mesures et Espace

• Se repérer dans l'espace
• Calculer des volumes
• Reconnaître une réduction ou un agrandissement
• Calculer des longueurs, des aires, des volumes d'un objet agrandi ou réduit
• Construire le patron d'un cône
• Les sections

Liens :

• Leçon : L'espace
• Préfixes qui servent à la composition des multiples et sous-multiples décimaux de nano à giga
• Activité : les 16 immeubles

Notions retravaillées :

Volume, Pythagore, Thalès, Équations, grandeurs

Attendu de fin de cycle : Exemples de réussite

L'élève pointe Paris et Sidney sur un globe terrestre à partir de leurs latitudes et longitudes. Il reconnaît un grand cercle sur une sphère. Il trace des solides en perspective cavalière et fait apparaître des sections.

Les fonctions

• Déterminer une fonction.
• Modéliser une situation de proportionnalité (fonction linéaire)
• Déterminer une image, un antécédent à partir d'une expression littérale, d'un tableau de valeurs, à partir d'une courbe.
• Reconnaître une fonction linéaire ou une fonction affine.
• Exploiter et construire une représentation graphique.

Liens :

• Leçon : Fonctions affines
• Exercices : Fonctions
• Exemples Geogebra

Notions retravaillées :

Proportionnalité, Calcul numérique

Attendu de fin de cycle : Exemples de réussite

À partir de l’allure de la représentation graphique d’une fonction affine, l'élève détermine le signe du coefficient directeur et l’ordonnée à l’origine.

Les transformations

• Construire l'image d'une figure par une translation, une symétrie (axiale et centrale), une rotation, une homothétie.
Construire des frises, des pavages, des rosaces

Liens :

• Rappels sur les transformations

Notions retravaillées :

Les transformations - les configurations de Thalès, la proportionnalité, les fonctions linéaires, les rapports d’agrandissement ou de réduction des grandeurs géométriques.

Attendu de fin de cycle : Exemples de réussite

L'élève détermine des longueurs, des aires, des mesures d’angles et des volumes en utilisant les propriétés de conservation des symétries (axiale et centrale), d’une translation, d’une rotation.

Dans une homothétie de rapport k, il calcule des longueurs, des aires et des volumes.

Par exemple, il est capable de calculer l’aire de la figure obtenue dans une homothétie de rapport k (k non nul) connaissant l’aire de la figure initiale.