Progression simplifiée

Progression 6ème

N°	Leçon	Lien + info
1	Nombres entiers	https://site2wouf.fr/entiers.php Lire, écrire, décomposer et comparer des entiers de grande taille.
2	Éléments de géométrie	https://site2wouf.fr/elements_geometrie.php Vocabulaire de base : point, segment, droite, appartenance, milieu.
3	Opérations sur les entiers naturels	https://site2wouf.fr/operations-entiers.php Poser et vérifier : additions, soustractions, multiplications, division euclidienne, divisibilité.
4	Nombres décimaux et opérations	https://site2wouf.fr/decimaux%26operations.php Introduire les décimaux, comparer, aligner les virgules, calculer et arrondir.
5	Parallèles et perpendiculaires	https://site2wouf.fr/paraperp.php Tracer avec précision.
6	Fractions	https://site2wouf.fr/fractions_6.php Du partage au nombre : lire, comparer à 1 et écrire sous forme mixte.
7	Fractions décimales. Division décimale	https://site2wouf.fr/division.php Relier fraction décimale et écriture à virgule ; poser une division longue.
8	Les angles	https://site2wouf.fr/angles.php Identifier, mesurer au rapporteur et construire ; bissectrice au programme.
9	Proportionnalité et gestion de données	https://site2wouf.fr/gestion_de_donnees.php Repérer une situation proportionnelle, coefficient, passage à l’unité, tableaux & représentations.
10	Symétrie axiale	https://site2wouf.fr/symetrie-axiale.php Construire des symétriques et connaître les propriétés de conservation.
11	Conversions	https://site2wouf.fr/conversions.php Changer d’unités (L, m, g, m², m³) et relier m³ et L sans pièges.
12	Aires et périmètres	https://site2wouf.fr/aires_perimetres_6.php Formules utiles (carré, rectangle, triangle), longueur du cercle et aire du disque.
13	Triangles et quadrilatères	https://site2wouf.fr/triangles_quadrilateres_cycle3.php Reconnaître, coder et construire triangles usuels et quadrilatères particuliers.
14	Pourcentages	https://site2wouf.fr/pourcentages.php Calculer une fraction d’une quantité et appliquer un pourcentage par plusieurs méthodes.
15	Solides et volumes	https://site2wouf.fr/solides.php Nommer les solides usuels, lire patrons et perspectives cavalières.
16	Initiation aux probabilités	https://site2wouf.fr/initiation_probabilites.php Vocabulaire, issues/événements, comparaison qualitative et premières proportions.
17	Priorités des opérations	https://site2wouf.fr/priorites.php Respecter l’ordre des opérations et l’effet des parenthèses.

Progression détaillée

Premier semestre

Nombres Entiers

Utiliser et représenter les grands nombres entiers
Règles d'orthographe
Décomposition

Attendu de fin d'année : Exemples de réussite

L'élève recopie la phrase suivante en écrivant le nombre en chiffres : « Au mois de juin 2018, la population mondiale est d’environ sept milliards cinq cent cinquante-neuf millions deux cent quatre-vingt-huit mille trois cents personnes. »

Liens

Notions retravaillées

l'orthographe des nombres

Compétences correspondantes

Modéliser- Modéliser en utilisant les langages mathématiques
Représenter- Produire et utiliser les représentations des nombres
Représenter- Passer d’un mode de représentation à un autre
Raisonner- Raisonner pour résoudre des problèmes
Communiquer- Communiquer en utilisant les langages mathématiques

Eléménts de géométrie

Le point
Le segment
la droite
La demi-droite
Appartenance
Milieu

Attendu de fin d'année : Exemples de réussite

L'élève code des figures simples :

les triangles (dont les triangles particuliers : triangle rectangle, isocèle, équilatéral) ;
les quadrilatères (dont les quadrilatères particuliers : carré, rectangle, losange).

Liens

Notions retravaillées

La géométrie de cycle 3.

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Modéliser- Modéliser pour résoudre des problèmes concrets
Raisonner- Justifier, Argumente

Opérations sur les entiers naturels

Addition
Addition à trou (Soustraction)
Multiplication
Division euclidienne
Divisibilité (Critères)

Attendu de fin d'année : Exemples de réussite

L'élève complète l’égalité : 3 dizaines de milliards et 8 millions = … millions

Liens

Notions retravaillées

Généralités sur les entiers

Compétences correspondantes

Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs

Nombres décimaux et opérations

Les entiers ne suffisent pas - Demi-droite graduée
Nom des chiffres dans l'écriture décimale
Comparaison de décimaux
Addition et soustraction des décimaux
Multiplication des décimaux

Attendu de fin d'année : Exemples de réussite

L'élève encadre le nombre 28,4597 :

par deux nombres entiers consécutifs ;
par deux nombres décimaux, au dixième près ;
par deux nombres décimaux, au centième près ;
puis, par deux nombres décimaux, au millième près.

L'élève est capable de répondre au problème suivant :

Paolo achète dans un magasin un DVD à 7,50 € et trois CD à 4,90 € l'unité. Combien va-t-il payer ?

Liens

Notions retravaillées

Les entiers naturels - Opérations sur les entiers

Compétences correspondantes

Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs
Représenter- Produire et utiliser les représentations des nombres
Communiquer- Communiquer en utilisant les langages mathématiques

Parallèles et perpendiculaires

Droites parallèles
Droites perpendiculaires
Propriétés
La médiatrice d'un segment

Attendu de fin d'année : Exemples de réussite

L'élève représente, reproduit, trace ou construit des figures simples.

Il représente, reproduit, trace ou construit des figures complexes (assemblages de figures simples)

Liens

Notions retravaillées

Les éléments de géométrie

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Représenter- Représenter des solides et des situations spatiales
Modéliser- Modéliser pour résoudre des problèmes concrets
Raisonner- Démontrer
Raisonner- Justifier, Argumenter

Fractions

Vocabulaire
Fractions et partage
Lecture d'une fraction
Une fraction est un nombre
Comparaison d'une fraction à l'unité
Écrire une fraction comme la somme d'un nombre entier et d'une fraction inférieure à 1

Attendu de fin d'année : Exemple de réussite

L'élève complète les égalités suivantes :

4 × … = 8 ; 4 × … = 10 ; 4 × … = 11

Liens

Notions retravaillées

Opérations sur les entiers naturels

Compétences correspondantes

Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Communiquer - Communiquer pour porter un regard critique
Chercher- Extraire des informations, les organiser, les confronter à ses connaissances
Chercher- Analyser un problème, décomposer un problème en sous problèmes

Fractions décimales. Division décimale

Fraction décimale
Division décimale

Attendu de fin d'année : Exemple de réussite

Sans utiliser le mot « virgule », l'élève lit et écrit de différentes façons le nombre 15,3062 :

15 unités et 3 062 dix-millièmes ;
153 062 dix-millièmes ;
\( 1 \times 10 + 5 \times 1 + \dfrac{3}{10} +\dfrac{6}{1000} +\dfrac{2}{10~000} \)
\( 15 + \dfrac{3~062}{10~000} \)

Liens

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour porter un regard critique
Calculer- Calculer avec des nombres
Chercher-Tester, essayer, valider, corriger une démarche

Les angles

Notion d'angles
Le rapporteur
La bissectrice

Attendu de fin d'année : Exemple de réussite

L'élève Construit un angle \( \widehat{AOB} \) de mesure 70° et un angle \( \widehat{COD} \) de mesure 150°.

Liens

Compétences correspondantes

Représenter- Passer d’un mode de représentation à un autre
Représenter- Produire et utiliser les représentations des nombres
Communiquer- Communiquer en utilisant les langages mathématiques
Modéliser- Modéliser pour résoudre des problèmes concrets
Modéliser- Modéliser en utilisant les langages mathématiques

Proportionnalité et gestion de données

Grandeurs proportionnelles
Tableau de proportionnalité
Les tableaux
Les représentation

Attendu de fin d'année : Exemple de réussite

Dans un collège, les enfants ont le choix d'étudier 3 langues pour la langue vivante 2 : italien, allemand ou espagnol.

En 5e A, il y a 25 élèves. 12 ont choisi espagnol, 6 allemand et les autres italien.
En 5e B, 13 élèves ont choisi espagnol et 5 élèves allemand.
Dans ces deux classes, 12 élèves ont choisi italien.

Présenter ces données dans un tableau à double entrée.

Liens

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Communiquer - Communiquer pour porter un regard critique
Chercher- Extraire des informations, les organiser, les confronter à ses connaissances
Représenter- Représenter pour résoudre des problèmes
Représenter- Passer d’un mode de représentation à un autre

Deuxième semestre

Symétrie axiale

Figures symétriques
Axes de symétrie
Points symétriques
Constructions
Propriétés
Symétrique d'un segment
Symétrique d'une droite
Symétrique d'un cercle
Symétrie et figures usuelles

Attendu de fin d'année : Exemple de réussite

Sur une feuille blanche, l'élève est capable de construire le symétrique d’un point, d’un segment, d’une droite ou d’une figure par rapport à un axe donné en utilisant l’équerre et la règle graduée ou le compas et une règle non graduée.

Il est capable compléter une figure comme ci-dessous pour tracer sa symétrique par rapport à la droite.

Pour tracer l’image de la figure précédente, il est capable de dire la symétrie axiale conservant les longueurs et les mesures angulaires il lui suffit de tracer les images des points A et B puis d’utiliser le quadrillage pour terminer sa construction.

Liens

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Représenter- Représenter des solides et des situations spatiales
Modéliser- Modéliser pour résoudre des problèmes concrets
Raisonner- Démontrer
Raisonner- Justifier, Argumenter

Conversions

Conversions d'unités de longueur
Conversion d'unités de masse et de contenance.
Conversions d'unité d'aire
Quelques unités de volume (cm³, dm³ et m³)
Relations entre unités de contenance et de volume

Attendu de fin d'année : Exemple de réussite

L'élève sait que :

1,5 km² correspond à 1 500 000 m² ;
10 m² correspondent à 0,1 dam² ;
145 cm² correspondent à 0,0045 m² ;
125 mm² correspondent à 0,25 cm² ;
13,12 dm² correspondent à 312 cm²

Liens

Compétences correspondantes

Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Communiquer - Communiquer pour porter un regard critique
Chercher- Extraire des informations, les organiser, les confronter à ses connaissances
Représenter- Représenter pour résoudre des problèmes
Représenter- Passer d’un mode de représentation à un autre

Aire et périmètre

I. Polygone
II. Le carré
III. Le rectangle
IV. Le triangle rectangle
V. Le triangle quelconque
VI. Le cercle. Le disque

Norions retravaillées

Les conversions

Attendu de fin d'année : Exemple de réussite

L'élève calcule, à l’aide de la formule et en utilisant 3,14 comme valeur approchée du nombre Pi, la longueur d’un cercle dont :

Le rayon est donné (par exemple par calcul mental dans le cas où le rayon est 5 cm, ou à l’aide d’une multiplication posée ou de la calculatrice dans le cas où le rayon est de 7,8 dm) ; (L1 ≈ 2 × 3,14 × 5 cm et L2 ≈ 2 × 3,14 × 7,8 m)
Le diamètre est donné (par exemple par calcul mental dans le cas où le diamètre est 20 cm, ou à l’aide d’une multiplication posée ou de la calculatrice dans le cas où le diamètre est de 9,6 m). (L3 ≈ 3,14 × 20 cm et L4 ≈ 3,14 × 9,6 m)

Liens

Compétences correspondantes

Représenter- Passer d’un mode de représentation à un autre
Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs
Calculer- Calculer avec des lettres, des algorithmes
Représenter- Produire et utiliser les représentations des nombres
Communiquer- Communiquer en utilisant les langages mathématiques
Modéliser- Modéliser pour résoudre des problèmes concrets
Modéliser- Modéliser en utilisant les langages mathématiques

Triangles et quadrilatères

I. Polygones
II. Les triangles
III. Les quadrilatères

Notions retravaillées

Les éléments de géométrie, les angles, la symétrie axiale.

Attendu de fin d'année : Exemples de réussite

À partir d’une description écrite, d’un programme de construction, l'élève est capable de faire une représentation à main levée codée et de construire à l’aide des instruments une figure simple.
Il Construit un carré dont les diagonales mesurent 5 cm.
Il Construit un losange ABCD dont les diagonales mesurent 6,4 cm et 3 cm
Pour construire le carré ABCD dont le côté mesure 8 cm, il est capable de dire ou d’écrire : « Je commence par tracer le segment [AB] mesurant 8 cm, puis la droite perpendiculaire à la droite (AB) passant par B, sur cette droite, je place un point C tel que BC = 8 cm… »

Liens

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Représenter- Représenter des solides et des situations spatiales
Modéliser- Modéliser pour résoudre des problèmes concrets
Raisonner- Démontrer
Raisonner- Justifier, Argumenter

Pourcentages

I. Fraction d'une quantité
II. Appliquer un pourcentage

Notions retravaillées

Les fractions, les fractions décimales, la proportionnalité

Attendu de fin d'année : Exemples de réussite

L'élève sait donner un ordre de grandeur de 48 % de 60,45 €.
Il sait calculer 13 % de 225 €.
Il sait calculer mentalement 50 % de 120 élèves (la moitié, diviser par 2) ; 25 % de 120 (le quart, diviser par 4), 10 % de 120 (le dixième, diviser par 10), 20 % de 120 (2 × 10 %, donc diviser par 10 et multiplier par 2)…
Un collège comporte 775 élèves. 24 % des élèves sont externes. Calcule le nombre d’élèves externes.

Liens

Compétences correspondantes

Communiquer- Communiquer en utilisant les langages mathématiques
Communiquer - Communiquer pour expliquer, argumenter et comprendre autrui
Communiquer - Communiquer pour porter un regard critique
Chercher- Extraire des informations, les organiser, les confronter à ses connaissances
Représenter- Représenter pour résoudre des problèmes
Représenter- Passer d’un mode de représentation à un autre

Solides et volumes

I. Introduction aux Solides Géométriques
II. Le pavé droit
III. Le prisme droit
IV. Le cylindre
V. La pyramide
VI. Le cône de révolution
VII. La sphère, la boule

Notions retravaillées

Droites parallèles, perpendiculaires - Conversions

Attendu de fin d'année : Exemples de réussite

Il est capable de dire que le solide suivant est constitué d’un cylindre surmonté d’un cône de sommet D, et que [DA] est la hauteur de ce cône.
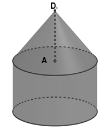
Il est capable de produire, un patron d’un pavé dont les dimensions sont données. Par exemple, pour le patron d’un pavé dont les dimensions sont 2 cm, 3 cm et 4 cm, il produit sur quadrillage ou sur papier blanc une figure comme ci-dessous.

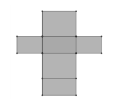
Liens

La leçon sur le site2wouf.fr

Compétences correspondantes

Représenter- Représenter des solides et des situations spatiales
Raisonner- Démontrer
Modéliser- Modéliser pour résoudre des problèmes concrets
Représenter- Représenter des solides et des situations spatiales

Initiation aux probabilités

I. Vocabulaire des probabilités
II. Notion de probabilité
III. Représenter les probabilités
IV. Applications et exercices types

Notions retravaillées

Les fractions

Attendu de fin d'année : Exemples de réussite

L'élève comprend et utilise le vocabulaire spécifique des probabilités. Il reconnaît une expérience aléatoire comme une expérience dont on connaît tous les résultats possibles mais dont on ne peut pas prévoir avec certitude le résultat qui se produira. Il identifie les issues (résultats possibles) et les événements (ensembles d'issues) d'une expérience simple.

Dans des situations concrètes et familières (lancer de dé, pièce de monnaie, tirage de boules colorées, roue de la fortune), l'élève sait :

Déterminer toutes les issues possibles d'une expérience aléatoire simple
Reconnaître des événements certains (probabilité = 1), impossibles (probabilité = 0) et probables
Comparer qualitativement les probabilités d'événements simples en utilisant le vocabulaire adapté : "plus de chances", "moins de chances", "autant de chances"
Placer des événements sur une échelle de probabilités allant d'impossible à certain

Pour des expériences simples avec équiprobabilité (toutes les issues ont la même chance de se produire), l'élève calcule des probabilités en utilisant la formule :

Probabilité = Nombre d'issues favorables / Nombre total d'issues possibles

Par exemple, il sait calculer :

La probabilité d'obtenir un nombre pair avec un dé à 6 faces : P = 3/6 = 1/2
La probabilité de tirer une boule rouge dans un sac contenant 4 rouges, 3 bleues et 2 vertes : P = 4/9
La probabilité d'obtenir "pile" avec une pièce équilibrée : P = 1/2 (une chance sur deux)

L'élève exprime une probabilité sous différentes formes : fraction (3/4), nombre décimal (0,75), pourcentage (75%) ou expression courante ("trois chances sur quatre"). Il comprend que la probabilité est toujours un nombre compris entre 0 et 1.

À travers des manipulations et des simulations simples, l'élève observe que lorsqu'on répète une expérience un grand nombre de fois, la fréquence d'apparition d'un événement se rapproche de sa probabilité théorique. Cette première approche des probabilités, nouvelle au cycle 3, pose les bases pour les approfondissements ultérieurs au cycle 4.

Liens

La leçon sur le site2wouf.fr

Compétences correspondantes

Chercher - Observer, expérimenter, émettre des hypothèses sur le caractère aléatoire d'une expérience
Modéliser - Traduire en langage mathématique une situation de hasard
Représenter - Utiliser différentes représentations (tableaux, arbres, listes) pour dénombrer les issues
Raisonner - Distinguer ce qui est certain, possible ou impossible dans une expérience aléatoire
Calculer - Déterminer des probabilités simples par le calcul de fractions
Communiquer - Utiliser le vocabulaire spécifique : expérience aléatoire, issue, événement, probabilité, équiprobable

Priorités des opérations

I. Additions et soustractions
II. Multiplications et divisions
III. Additions, soustractions et multiplications
IV. Parenthèses

Notions retravaillées

Les opérations sur les décimaux

Attendu de fin d'année : Exemples de réussite

L'élève sait utiliser une calculatrice pour introduire la priorité de la multiplication sur l'addition et la soustraction. Il comprend et explique pourquoi des calculs comme 3+4×8 donnent des résultats différents selon qu'on les effectue mentalement de gauche à droite (56) ou avec une calculatrice qui respecte les priorités (35). Il apprend à organiser un calcul en une seule ligne, utilisant si nécessaire des parenthèses.

Dans des expressions simples, l'élève applique correctement les règles de priorité : il effectue d'abord les calculs entre parenthèses, puis les multiplications et divisions de gauche à droite, et enfin les additions et soustractions de gauche à droite. Par exemple, il calcule correctement :

5 × 6 + 3 = 30 + 3 = 33
5 × (6 + 3) = 5 × 9 = 45
12 + 8 × 3 - 4 = 12 + 24 - 4 = 32

L'élève sait également gérer des parenthèses emboîtées simples, en commençant par les parenthèses les plus intérieures : 3 × (5 + (6 - 5)) = 3 × (5 + 1) = 3 × 6 = 18. Dans des calculs simples, confrontés à des problématiques de priorités opératoires, par exemple en relation avec l'utilisation de calculatrices, les élèves utilisent des parenthèses.

L'élève distingue et nomme correctement les résultats des opérations : somme pour l'addition, différence pour la soustraction, produit pour la multiplication et quotient pour la division. Il identifie la nature d'une expression en fonction de la dernière opération effectuée.

Liens

Compétences correspondantes

Calculer- Calculer avec des nombres
Calculer- Contrôler les calculs
Calculer- Calculer avec des lettres, des algorithmes
Chercher-Tester, essayer, valider, corriger une démarche

site2wouf.fr : Progression 6ème

Progression 6ème

Nombres entiers

Éléments de géométrie

Opérations sur les entiers naturels

Nombres décimaux et opérations

Parallèles et perpendiculaires

Fractions

Fractions décimales. Division décimale

Les angles

Proportionnalité et gestion de données

Symétrie axiale

Conversions

Aires et périmètres

Triangles et quadrilatères

Pourcentages

Solides et volumes

Initiation aux probabilités

Priorités des opérations

Premier semestre

Nombres Entiers

Attendu de fin d'année : Exemples de réussite

Liens

Notions retravaillées

Compétences correspondantes

Eléménts de géométrie

Attendu de fin d'année : Exemples de réussite

Liens

Notions retravaillées

Compétences correspondantes

Opérations sur les entiers naturels

Attendu de fin d'année : Exemples de réussite

Liens

Notions retravaillées

Compétences correspondantes

Nombres décimaux et opérations

Attendu de fin d'année : Exemples de réussite

Liens

Notions retravaillées

Compétences correspondantes

Parallèles et perpendiculaires

Attendu de fin d'année : Exemples de réussite

Liens

Notions retravaillées

Compétences correspondantes

Fractions

Attendu de fin d'année : Exemple de réussite

Liens

Notions retravaillées

Compétences correspondantes

Fractions décimales. Division décimale

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Les angles

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Proportionnalité et gestion de données

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Deuxième semestre

Symétrie axiale

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Conversions

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Aire et périmètre

Norions retravaillées

Attendu de fin d'année : Exemple de réussite

Liens

Compétences correspondantes

Triangles et quadrilatères

Notions retravaillées

Attendu de fin d'année : Exemples de réussite

Liens